РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ В 9 КЛАССЕ С ПРИМЕНЕНИЕМ MATHCAD

Квадратные неравенства являются важной частью школьной программы по алгебре в 9 классе. Они требуют от учеников не только знания теории, но и навыков решения задач, которые могут быть сложными и трудоемкими [6].

В современном мире информационных технологий использование специализированного программного обеспечения, такого как Mathcad, может значительно облегчить этот процесс.

Для начала разберем, что такое квадратные неравенства.

Квадратным называется неравенство вида:

 

ax²+bx+c>0 или ax²+bx+c<0,

 

где a, b и c ‑ коэффициенты, причем a ≠ 0 [3].

Для решения квадратного неравенства необходимо:

1. Найти корни соответствующего квадратного уравнения (ax²+bx+c=0).

2. Определить знаки выражения (ax²+bx+c) на промежутках, определяемых корнями уравнения.

3. Выбрать те промежутки, на которых выражение удовлетворяет заданному неравенству [4].

Mathcad ‑ это мощный инструмент для математических вычислений, который позволяет решать уравнения и неравенства, строить графики и выполнять множество других операций [7].

Рассмотрим шаги решения квадратного неравенства с помощью Mathcad.

Шаг 1. Ввод коэффициентов.

Начнем с ввода коэффициентов (a), (b) и (c) в Mathcad. Например, для неравенства (2x² - 3x - 2 ≥ 0) коэффициенты будут:

 

 

Шаг 2. Определение функции.

Определим функцию, соответствующую квадратному уравнению:

 

 

Шаг 3. Нахождение корней квадратного уравнения.

Используем формулу для нахождения корней квадратного уравнения [2]:

 

 

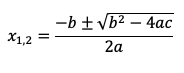
В Mathcad это можно записать следующим образом:

 

 

Шаг 4. Построение графика.

1. Перейдем на вкладку «Plots» (Графики) в верхнем меню Mathcad.

2. Выберем «2D Plot» (2D график) и щелкнем в рабочей области, чтобы вставить график.

3. В появившемся графике щелкнем на оси X и введем диапазон значений, например, от (x₂ - 2) до (x₁ + 2):

 

 

4. Щелкнем на оси Y и введем функцию (f(x)):

 

 

Шаг 5. Настройка графика.

1. Щелкнем правой кнопкой мыши на графике и выберем «Format» (Формат).

2. В разделе «Grid» (Сетка) установим желаемый шаг сетки по осям X и Y, например, 0.5 для X и 1 для Y.

3. Нажмем «OK» для применения изменений.

Шаг 6: Анализ графика

1. На графике увидим параболу, открывающуюся вверх.

2. Определим области, где функция ( f(x) ) принимает значения больше или равные нулю. Это и будет область, где неравенство (2x² - 3x - 2 ≥ 0) выполняется.

Приведем полный пример программы в Mathcad.

 

 

Следуя этим шагам, сможем визуализировать решение неравенства и определить области, где оно выполняется.

Использование программного обеспечения Mathcad для решения квадратных неравенств имеет свои преимущества и недостатки. Рассмотрим их подробнее.

Преимущества:

1. Автоматизация вычислений. Mathcad позволяет автоматизировать процесс вычислений, что значительно снижает вероятность ошибок, связанных с ручными расчетами. Это особенно полезно при работе с сложными уравнениями и неравенствами.
2. Визуализация. Mathcad предоставляет мощные инструменты для построения графиков и визуализации данных. Это помогает лучше понять поведение функции и наглядно увидеть решение неравенства.
3. Удобство и скорость. Mathcad позволяет быстро и удобно вводить данные и получать результаты. Это экономит время и усилия, которые можно направить на анализ и интерпретацию результатов.
4. Интерактивность. Mathcad поддерживает интерактивные вычисления, что позволяет легко изменять параметры и мгновенно видеть, как это влияет на решение. Это полезно для экспериментов и исследования различных сценариев.
5. Документирование. Mathcad позволяет создавать хорошо структурированные документы, включающие как вычисления, так и текстовые комментарии. Это делает результаты более понятными и легко воспроизводимыми.
6. Обучение и развитие навыков. Использование Mathcad способствует развитию навыков работы с современными математическими инструментами, что полезно для дальнейшего обучения и профессиональной деятельности [5].

Недостатки:

1. Стоимость. Mathcad является коммерческим программным обеспечением, и его лицензия может быть дорогой для учебных заведений и частных пользователей.
2. Сложность освоения. Mathcad имеет богатый функционал, который может быть сложным для новичков. Требуется время и усилия для освоения всех возможностей программы.
3. Зависимость от программного обеспечения. Использование Mathcad может привести к зависимости от программного обеспечения. Ученики могут стать менее уверенными в своих навыках ручного решения задач.
4. Ограниченная доступность. Не все учебные заведения и ученики имеют доступ к Mathcad, что может ограничить его использование в учебном процессе.
5. Технические требования. Mathcad требует определенных технических ресурсов, таких как мощный компьютер и операционная система, что может быть проблемой для некоторых пользователей [5].

Не смотря на имеющийся ряд недостатков, использование Mathcad для решения квадратных неравенств в 9 классе позволяет значительно упростить процесс вычислений и визуализации. Ученики могут сосредоточиться на понимании теоретических аспектов и логике решения задач, а Mathcad возьмет на себя рутинные вычисления. Это не только повышает эффективность обучения, но и развивает навыки работы с современными математическими инструментами.

Таким образом, интеграция Mathcad в процесс обучения алгебре в 9 классе является полезным и перспективным шагом, который способствует более глубокому и качественному усвоению материала.