Метод ближайших соседей. Временами базисом случайного поведения комплекса является динамический беспорядок, который может начинаться, в частности, нелинейными системами простейших уравнений в производных. Предположим, имеется заданный процесс развития, происходящий в N-мерном пространстве. Данный процесс определяется комплексом, состоящим из N дифференциальных уравнений. Неопределенным имеет место N-мерный вектор x = (x1, x2, x3, …, xN). На производстве, особенно для экономических течений, состав таких уравнений не известен, если вопрос не стоит о чисто математическом фантоме. Известно, что значение одной из компонент ситуации вектора x, например, x, взятой через одинаковые интервалы времени :
x(t), x(t + t ), x(t + 2t ),..., x(t + (d - 1)t ),..., x(t + (N - 1)t ) .
Из одномерного промежуточного ряда выстраиваем ряд c-мерных векторов, базисами каждого из данных векторов являются с последовательные элементы заданного ряда x. Так, первым из векторов будет:
y1 = ( x(t), x(t + t ),..., x(t + (d - 1)t )),
y 2 = ( x(t + t ), x(t + 2t ),..., x(t + dt ))
Поскольку величина N часто не определена, то выполняют поэтапное возрастание величины размерности с, например, до постоянства корреляционной базируемости. Найдем значение данной величины корреляционной размерности общим методом [6]:

Рис. 1. Прогнозируемые данные — Y и истинные — x на 7 дней вперед для курса доллара к рублю
(по Центробанку России) на 20, 21, 22, 26, 29, 30 и 31 мая 2020 г.
По оси абсцисс — дни, а по оси ординат — курс доллара к рублю
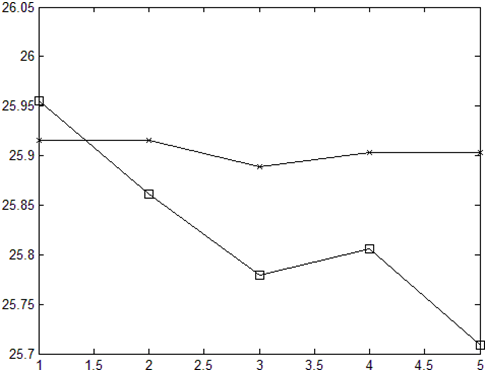
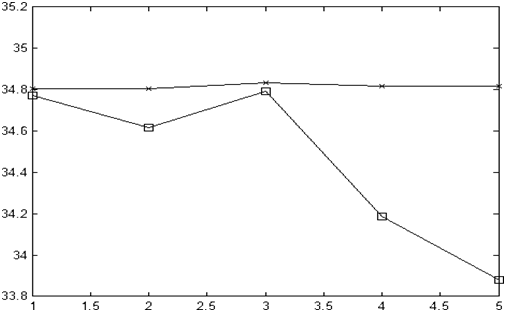
Рис. 2. Прогнозируемые данные — Y и истинные — x на 7 дней вперед для курса евро к рублю
(по Центробанку России) на20, 21,27, 28, 29, 30 и 31 мая 2020 г. По оси абсцисс — дни, а по оси ординат — курс евро к рублю
Заключение:
Результаты математического фантомирования показали, что применение копий рядом находящихся соседей разрешает делать положительный анализ на трое суток вперед при наличии последовательного беспорядка в курсах валют. Модель ARIMA не рекомендуется применять в рассмотренной ситуации.
Список литературы
- Балонишников А. М., Балонишникова В. А. Моделирование обменных курсов основных валют // Журнал прикладной информатики. 2010. № 1(25). С.1520.
- Безручко В. П., Смирнов Д. А. Математическое моделирование хаотических временных рядов Саратов: Гос УНЦ «Колледж», 2005. 532 с.
- Григорьев В. П., Козловских А. В., Марьясов Д. А. Исследование математической модели фью- черсных рынков //Рынок ценных бумаг. 2005. № 9(288). С.3842.
- Малинецкий Г. Г., Потапов А. Б., Подлазов А. В. Нелинейная динамика. Подходы, результаты, надежды. М.: КомКнига, 2006.
- Халафян А. А. STATISTICA 6. Статистический анализ данных. М.: Бином, 2010.
- Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988.
- Box G. E. P., Jenkins C. M. Time series analysis: Forecasting and control. San Francisco: Holden-Day, 1970.
- Brock W. A. Distinguishing random and deterministic systems // Journal of Economic Theory. 1986, Vol. 40. P.168195.
- Brock W. A. Nonlinearity and complex dynamics in economics and finance // Evolving Complex Sys- tems. Anderson P.W., Arrow K. And Pines A. eds. pp.7797.
- Brock W. A., Dechert W.D. and Scheinkmann J. A test for independence, based on correlation dimen- sion. SSRI Working Paper N 8702. University of Wisconsin, 1987.



