Вайолет Констанс Джессоп работала стюардессой на океанских лайнерах именитой на тот момент компании «White Star Line». Той самой компании, которой принадлежал «ТИТАНИК». 20 сентября 1911 года корабль Олимпик совершил столкновение с другим судном. Олимпик, на котором работала Вайолет, отправился на ремонт, а она сама перевелась на Титаник. В 1912 году она отправилась в первое и последнее плавание Титаника. Вайолет оказалась одной из тех, кому удалось спастись. В 1916 году она оказалась на Британике. 21 ноября 1916 года Британик наткнулся на мину. Капитан принял решение попытаться добраться до берега, но в это время уже несколько шлюпок с пассажирами были спущены на воду, из-за этого их начало затягивать под гребные винты. Вайолет как раз была в одной из шлюпок и незадолго до того, как шлюпка попала под винт она выпрыгнула из неё. Это решение далось ей крайне тяжело ведь она не умела плавать… После всех этих историй Вайолет продолжала работать на кораблях и дожила до глубокой старости, умерла в возрасте 83 лет.
Инспектора по охране национального парка Рой Салливан за 35 лет работы там била молния 7 раз, и каждый раз он оставался жив.
Посчитаем вероятность того, что молния ударит в случайного человека и он выживет:
В целом в год молнии ударяют 1400000000 раз. Из них 200 000 попадают в людей. Из этих 200 000 остаются в живых 190 000.
A={Человек выжил при ударе молнии}
m-количество выживших людей при ударе
n-количество людей, которых ударил молний
по формуле: P(A)=m/n, значит P(А̅ )=20000/200000=1/10=0.1
Значит P(A)=1-P(А̅ )=1-0,1=0.9
Это мы нашли вероятность выживания при ударе молнии.
По теории вероятность он мог умереть на 10-ый раз.
Но вот вероятность попадания молнии 7 раз в одного человека уже гораздо меньше и она стремится к нулю.
В городе Туксон учёные выяснили, что из 386 молний 136 ударяли в одно и тоже место 2 или более раз.
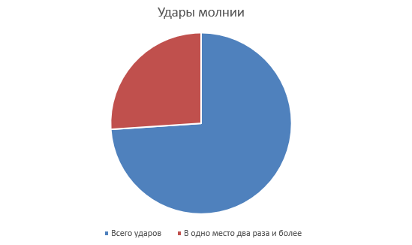
График 1. Удары молнии в городе Туксон
По формуле вероятности:
m-количество раз, когда молния ударяет в одно и тоже место более 2 раз
n-общее количество ударов молнии
A=(молния ударила более 2 раз в одно место)
P(A)=m/n
P (A) = 136/386=0,35233
Получили вероятность события А в тот вечер в городе Туксон.
«Где в следующий раз ударит молния?». На этот вопрос ещё никто не смог бы ответить с точностью до миллиметра. Это связано с тем, что человек просто не способен просчитать траекторию движения каждой молекулы в воздухе.
Альберт Эйнштейн не верил в случайности, обосновывая это тем, что человек просто не знает всех закономерностей во вселенной, а когда узнаем, то место случайности не останется.
Попытаемся разобраться, так ли это или нет?
Орёл и Решка.
Мы часто прибегаем к этому просто методу принятия решения. Пусть Орёл - это идти на пару по математике, а Решка-не идти. Подбросили монету, нам выпал Орёл.
Пусть Орёл-писать красной ручкой, а Решка-синей.
Подбросили монету, нам выпала Решка.
При броске вручную идеально правильная монета должна всегда выдавать одинаковую вероятность выпадения «Орла» и «Решки»
Попросим наших одногруппников придумать случайную последовательность Орёл-Решка:
Пример
Одногруппник 1: ОРОРООРРОР
Одногруппник 2: ОРОРРООРОР
Реальный опыт: РООООРОРОО
В первых двух случаях соотношение орла к решке практически одинаковое, а в реальном опыте орёл выпал 4 раза подряд, а суммарно 7, а решка всего 3.
Последовательности легко отличить друг от друга. У человека работает интуиция, которая буквально подсказывает, что не может выпадать всегда одно и то же. Этот феномен даже получил своё научное название.
«Ложный вывод Монте-Карло», — ошибочное ощуещние того, что если какой-то случайный результат эксперимента повторяется слишком часто, то в другой раз он не повторится. Человек думает, что один исход события не может повторяться так часто, поэтом надо ставить на другой исход.
Если много раз выпадает Орёл, то пора бы и Решке, хотя на самом деле вероятность будет оставаться той же самой.
Таким образом мы видим, что мозг не так уж хорошо справляет с задачами на случайность, из-за интуиции. Однако есть задача и посложнее. Придумать случайное число.
Случайное число
Кажется, что цифры: «7, 9, 11 ,17, 19, 86» более случайны, чем «10, 15, 100». Человеку сложно придумать короткую последовательность случайных чисел, т.к. он подсознательно будет сравнивать их и думать, что более случайно. Но если нам нужны эти случайные числа. А ведь они действительно нужны. Вспомните ту самую СМС-ку с кодом из 4 цифр от банка для подтверждения оплаты.
Есть два способа получения случайных чисел: Математический и Физический.
Математический способ – это простые математические формулы.
Пример
Возьмём число 122. Возводим его в квадрат. Получаем: 1222=14884. Далее убираем цифру, которая находится посередине. Получаем 1484.
Мы получили случайное число, ведь мы сами придумали алгоритм его получения. Вот только есть один нюанс. Для человека, знающего этот алгоритм, следующее число будет уже не случайным. Любой алгоритм можно предугадать и он начнет зацикливаться. Математический способ не так совершенен, как это требуется в настоящее время.
Физический способ - это способ хауса. Если мы выйдем на улицу, то там присутствует множество погодных явлений, которые мы можем измерить, оцифровать и обработать. Если производить с ними один и тот же алгоритм, то мы постоянно будем получать случайные числа. Волны, ветер, молнии, колебания атомов-всё это хаус, который получил название энтропия. Один сайт по генерации случайных чисел берёт за энтропию атмосферный шум, который возникает под ионосферой после грозового разряда. Каждую секунду на Земле вспыхивает порядка 40 молний => в день это порядка 3500000.
Для простых повседневных задач нам отлично подходит математический способ, но для более сложных, таких как: шифрование смс от банка, программирование боеголовок, выбор победителя в случайной лотерее или розыгрыше.
Заключение
В данной статье мы рассмотрели два основных метода получения случайного числа и сравнили их. На данный момент самым совершенным является метод физический. Ведь только природа способна породить настоящий хаус, который человек пока не может просчитать. Но кто знает, может быть когда-то мы узнаем траекторию движения каждой молекулы во Вселенной.
Список литературы
- Тутубалин, В. Н. Теория вероятностей / В.Н. Тутубалин. - М.: Издательство МГУ, 2016. - 232 c.
- Гренандер, У. Краткий курс вычислительной вероятности и статистики / У. Гренандер, В. Фрайбергер. - М.: Главная редакция физико-математической литературы издательства "Наука", 2016. - 192 c.
- YouTube. (2017, 6 июня). КАКОЕ АБСОЛЮТНО СЛУЧАЙНОЕ ЧИСЛО? —ТОПЛЕС [Видео файл]. Взято из https://www.youtube.com/watch?v=eRFgIh-raT8&t=541s



