USING BLENDER FOR LEARNING MATHEMATICS

Introduction

Modern 3D packages are multifunctional tools that can be used not only for visualization but also for exploring applied, exact, and fundamental sciences. Mathematics is no exception; virtually everything that surrounds us is connected to it, and software is no exception.

Software like Blender can significantly simplify the understanding of mathematical formulas because you use them in practice and see the results of the calculations immediately.

Tools

In this article, we will primarily explore the tools of 3D packages using Blender 3D as an example. The tools demonstrated are also present in other programs (3ds Max, Maya, Substance 3D Designer, etc.). The main tools that allow for the study of mathematics through simple practical examples in 3D packages are modifiers and nodes.

Nodes are part of the user interface (UI), graphical blocks that can be connected to each other. This tool enables the creation of procedural textures or geometry of varying complexity.

Modifiers are tools for interacting with the geometry of a model. Like the node system, it is a very powerful tool designed to save time and effort in creating and modifying objects. Today, it is almost impossible to do without this tool, as it greatly simplifies and automates both routine and very complex tasks.

Boolean Operations

Perhaps one of the most frequently used tools is Boolean algebra. It's hard to imagine any software suite where they are not employed.

In Blender, Boolean algebra is used to create complex geometric shapes through union, subtraction (difference), or intersection of objects. The Boolean tool checks

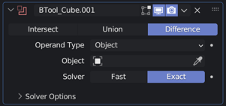
Boolean Interface

 

1. Difference A \ B = {x | x ∈ R³, x ∈ A и x ∉ B} 

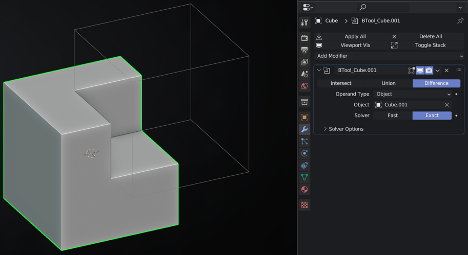
Example of Operation difference

 

2. Union A ∪ B = {x | x ∈ R³, (x ∈ A) или (x ∈ B)}

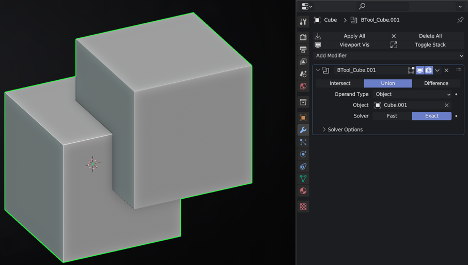
Example of Operation union

 

3. Intersect A ∩ B = {x | x ∈ R³, (x ∈ A) и (x ∈ B)}

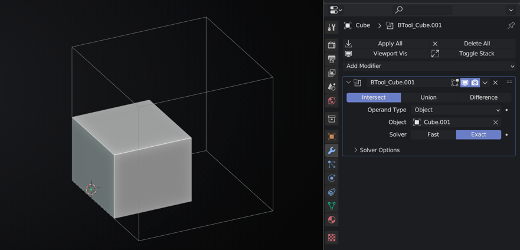
Example of Operation intersect

• A and B - geometric objects in three-dimensional space;
• R³ - represents three-dimensional space;
• x - a point in three-dimensional space.

When using these formulas, Blender searches for points of contact between the original model A and model B, relative to which the operation occurs. All these operations can be combined, allowing for the creation of interesting shapes.

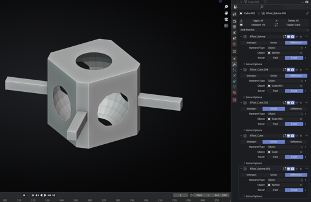
Example of Operation Boolean

Mathematical Nodes

In Blender, there are two types of nodes: geometry nodes and shader nodes.

Geometry nodes are used for working with the geometry of 3D models.

Shader nodes are used for creating shaders (textures). You can work with both tileable (repeating) textures and create procedural textures that are generated randomly.

In Blender, for all types of node systems, there are common basic mathematical nodes. Let's look at examples using shader nodes.

The Math node is fundamental, and a large number of different operators make it versatile.

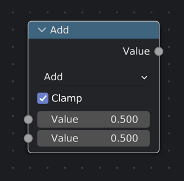
Node Math

 

Operators Math

 

By knowing the formulas of geometric shapes, you can use mathematical nodes to create textures with patterns.

 

1. Equation of a Rhombus: |x| + |y| = 1

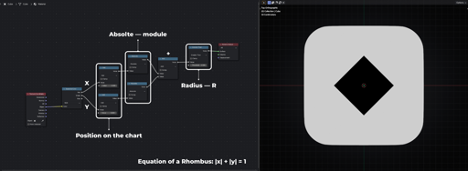
Texture in the Shape of a Rhombus

 

Texture Coordinate is not considered a mathematical node; it defines the type of projection onto the model, where in this case, the Object type analyzes the geometry of the object taking into account modifiers.

Through the Separate XYZ and Separate Color nodes, the texture is logically divided into three vectors (X, Y, Z), the values of which can be manipulated individually.

Using the Add operator (addition operator), the position on the XY axes is defined. In this case, the center of the figure is at the center of the graph. This node can be replaced with a separate Value node. 

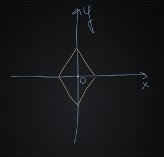
2D Projection of a Rhombus onto a Plane

 

The Absolute operator indicates that the values provided before it are in absolute terms (|x| and |y|).

Next, in the Math node with the Add operator, it is used to combine two branches of nodes and acts as an addition operation.

The resulting node network is then connected to a Greater Than node, where the Threshold parameter acts as R — the radius. In this case, the radius is set to 0.5.

All these nodes ultimately generate the formula: |x| + |y| = 0.5.

Material Output — the final output of the projection in the preview window, without this node, the object would be completely colored in black.

2. Equation of a Circle: x² + y² = R²

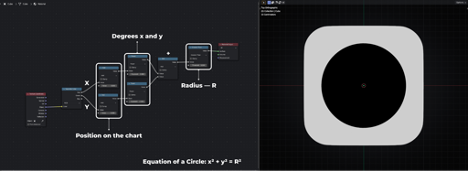
Texture in the Shape of a Circle

 

The only difference from the previous example is that here, instead of using the Absolute operator to take the modulus, the Power operator is used to raise x and y to powers.

 

Conclusion

This article provides an overview of the use of Blender in the practical teaching of mathematics. Originally developed as software for creating three-dimensional graphics, Blender proves to be a useful tool for visualizing and demonstrating mathematical concepts.
The advantages of using Blender 3D in mathematics education include its visual clarity, interactivity, and the ability to create complex three-dimensional scenes. The article also highlights the importance of the practical application of mathematical knowledge and contributes to the development of students' skills in modeling, visualization, and data analysis.
Overall, the article demonstrates the potential of Blender 3D in mathematics education, enriching the learning process and stimulating students' interest in mathematics through the practical application and visualization of complex mathematical concepts.