ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ ФАНТОМОВ ПРИ РАССМОТРЕНИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Уравнения в производных часто имеют место в фантомах финансовой динамики, в которых анализируются не только взаимосвязь переменных от времени, а и от их взаимосвязи во времени. Такими фантомами являются: копия Эванса — принятие уравновешенной стоимости на рынке одного продукта; а также динамический фантом финансового роста, известная под названием «стандартная копия Солоу».

В фантоме Эванса представлен рынок одного продукта, время является непрерывным. Пусть d(t), s(t), p(t) — спрос, предложение и цена соответственно данному  продукту на момент времени t. Предположим, что спрос и предложение являются линейными зависимостями цены, то есть d(p)=a-bp, a, b>0 — спрос с увеличением стоимости снижается, а s(p)=a+bp, где a, b>0 — предложение с прогрессированием цены увеличивается. Естественным имеет место соотношение а> 0, то есть при нулевой стоимости спрос опережает предложение.

Рассмотрим фантом Эванса закрепления равновесной стоимости на рынке одного продукта с постоянным временем t. Если спрос  и предложение  являются линейными прямыми цены p, то динамика стоимости представляется следующими уравнениями:

                                         

 

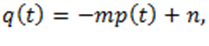
где 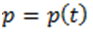  – цена товара в момент времени t.

Считаем, что 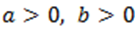  — предложение с поднятием цены растет;  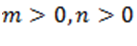 — спрос с ростом стоимости снижается. Кроме того, нужно считать  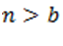 — при нулевой стоимости спрос превышает предложение.

Главное предположение фантома состоит в том, что изменение стоимости пропорционально опережению спроса над предложением:

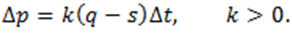
Согласно данной гипотезе отношение потребителей и производителей происходит таким образом, что отражающая это отношение стоимость непрерывно адаптируется к положению на рынке: в случае увеличения спроса над предложением — повышается, в противоположном случае — снижается.

Составим следующее  уравнение в производных относительно цены:

Данное уравнение содержит одну стационарную точку:

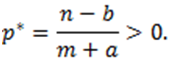
 Стоимость равновесия — абсцисса точки взаимодействия прямых спроса и предложения, т.е. при такой стоимости спрос отождествляется предложению.

 

Условие равновесия состоит в том, что предложение услуг   приравнивается спросу на услуги E:

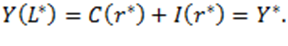
В копии Кейнса спрос на товары Е находит уровень занятости L, в отличие от стандартной модели, в которой действительная заработная плата, как отношение ставки заработной платы к цене продукта (w/p) , задавала число занятых.

В фантоме Кейнса равновесие на рынке услуг достигается при равенстве желаемого спроса и фактического предложения:

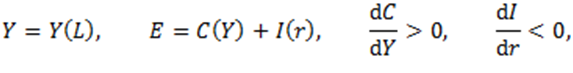
Фантом Солоу заключается в следующих уравнений, характеризующих экономическую динамику.

1.Количество предложения на рынке благ описывается производственной функцией с постоянной отдачей от масштаба:

Yt = F(Kt, L t)

для любого положительного Z верно:

Z Yt = F (ZКt, ZLt)

Предположим, что, тогда получим:

Yt/Lt = F(Kt/Zt,1), (3)

где Yt/Lt — производительность (у); Kt/Zt — капиталовооруженность (фондовооруженность) (k).

Уравнение (3) доказывает, что количество производства в расчете на одного сотрудника является задачей имущества на одного сотрудника.

В заключение хотелось бы выделить важную роль дифференциальных уравнений при решении большинства прикладных задач, так как довольно не всегда удается получить линейную функциональную зависимость между желаемыми и данными переменными величинами, но зато получается вывести  уравнение в производной, помогающее с наибольшей вероятностью описать течение определенного процесса при конкретных условиях.