Метеорологическая служба докладывает о движении двух грозовых очагов в сторону города, в котором, согласно плану, воздушное судно должно совершить посадку. Диспетчер докладывает о 3-х активных аэродромах (далее, а/д) и сообщает, что над двумя из них будет грозовая облачность и дает право на удачу выбрать аэродром прибытия. Пилот делает свой выбор (например, аэродром 1), в процессе полета диспетчер доложил о грозовой активности в соседнем активном а/д (например, 3) и сообщает о возможности изменить свой выбор из оставшихся двух активных а/д. Как, основываясь на теории вероятности, пилоту принять наиболее правильное решение?
Возможное решение:
Пусть пилот выбрал а/д №1. То, что на а/д №1 благоприятная погода - есть гипотеза A. Диспетчер сообщил информацию о грозовой деятельности на а/д №3 - это событие B.
Вероятность P(A|B) того, что на а/д №1 благоприятная погода после того, как стало известно, что на а/д №3 гроза (диспетчер сообщил информацию об а/д №3), равна:
P(A|B)= P(B|A) * P(A) / P(B)
P(A) - (до информации от диспетчера) вероятность того, что на а/д №1 благоприятная погода, равна 1/3, поскольку очевидно, что до получения информации вероятность благоприятной погоды на а/д №1 была равна 1/3 из условия равновероятности нахождения гроз в каждом аэропорту.
P(B|A) - вероятность того, что диспетчер сообщит об аэропорту №3, если событие A - истинно. Это равно 1/2, поскольку тогда диспетчер должен сообщить о любом из а/д №2 и №3, в которых наблюдается гроза.
P(B) - полная вероятность того, что диспетчер сообщил информацию о грозовой деятельности на а/д №3, равна сумме вероятностей того, что произойдет B (гроза на а/д №3) в результате реализации некоторых гипотез умноженных на вероятности этих гипотез.
Имеем три гипотезы (они несовместны, их суммарная вероятность равна 1):
1) На а/д №1 хорошая погода 2) На а/д №2 хорошая погода 3) На а/д №3 хорошая погода. Их вероятности равны 1/3. Вычислим условные вероятности:
Если на аэродроме №1 хорошая погода, то диспетчер сообщил об а/д №3 – вероятность 0.5 (т.к. у диспетчера 2 варианта)
Если на аэродроме №2 хорошая погода -> то диспетчер сообщил об а/д №3 - у диспетчера 1 вариант - сообщить об а/д №3, поскольку сообщить об а/д, на который летит пилот (аэродром №1) он не может - вероятность 1
Если на а/д №2 хорошая погода -> то диспетчер сообщил об а/д №3 -- вероятность 0%, поскольку ведущий не может сообщить об а/д с хорошей погодой. И того:
P(B) = 0.5 * 1/3 + 1 * 1/3 + 0 * 1/3 = 3/6 = 1/2
P(A|B)= 1/2 * 1/3 / (1/2) = 1/3
Тогда, вероятность того, что на 2-ом а/д хорошая погода: 1 - 1/3 = 2/3. Поэтому пилоту стоит сменить выбор!
Алгоритмизация задачи:
Данный алгоритм, написанный на языке программирования Python (рисунок 1), реализует задачу на практике. Сначала программа случайно распределяет грозы среди 3-х аэродромов. Также случайно выбирается первоначальный аэродром посадки, а затем алгоритм разделяется: искусственный интеллект сначала предпочитает не менять свой выбор, из-за чего, как можно заметить, из 100000 экспериментов «победить» удалось 33173 раз (число случайно и меняется при каждом новом запуске алгоритма), затем меняет выбор, побед оказалось примерно в 2 раза больше (рисунок 2).
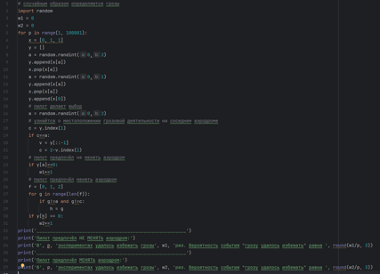
Рисунок 1. Алгоритм, реализующий задачу

Рисунок 2. Один из выведенных результатов работы алгоритма
Список литературы
- Геленбе Э. "Вероятностные модели и их применение в авиации." В Международной конференции по количественной оценке систем, с. 1-12. Springer, Cham, 2012
- Накагава М. "Использование вероятностной оценки рисков для обеспечения безопасности гражданской авиации." Надежность и безопасность систем 44, № 1 (1994): 91-106
- Демей М. и др. "Роль вероятности в авиационной безопасности." Управление рисками 14, № 1 (2012): 19-35



