РЕШЕНИЕ ЗАДАЧИ С ПАРАМЕТРОМ ЗА 5 МИНУТ

В данной статье разберемся со следующей задачей.

Задача. Найдите все значения a, при каждом из которых система неравенств

имеет единственное решение. (Профильный уровень, 36 вариантов, под ред. И. В. Ященко, Вариант 7) [2, с. 38].

Идеей для поиска другого подхода к решению этой задачи с параметром из ЕГЭ по математике послужил громоздкий на вычисления и рассуждения разбор данной задачи в сборнике типовых экзаменационных вариантов под редакцией И. В. Ященко. Рассмотрим решение, предложенное нами.

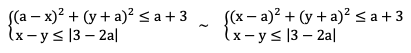
Первое неравенство системы определяет замкнутый круг при a+3>0 и точку при a+3=0, т.е. замкнутый круг вырождается в центр этого круга, который будет иметь координаты M₀ (-3;3).

Замечание. В нашем случае центр этого круга бегает по прямой y=-x и поэтому точка M₀ принадлежит данной прямой.

Второе неравенство определяет полуплоскость, т.е. верхнюю часть прямой y=x-|3-2a|, включая эту прямую.

Отметим, что задача имеет не более двух значений параметра a, при каждом из которых система неравенств имеет единственное решение: первое значение будет, если центр вырожденного круга т. M₀(-3;3) принадлежит полуплоскости y≥x-|3-2a|, это при a=-3; второе значение будет тогда, когда центр круга будет находиться в полуплоскости y<x-|3-2a| и на расстоянии от прямой y=x-|3-2a|, равном . В других случаях задача не имеет решений или имеет бесчисленное множество решений.

Реализуем этот план.

1) M₀(-3;3) принадлежит полуплоскости y≥x-|3-2a|,

3≥-3-|3-2a|, 3≥-12,

т.е. при a=-3 наша система имеет единственное решение.

2) а) Центр круга O(a;-a), находящийся ниже прямой y=x-|3-2a|, т.е. находящийся в полуплоскости y<x-|3-2a|.

б) Расстояние от центра круга O(a;-a) до прямой x-y-|3-2a|=0(l), равно .

Также рассмотрим решение аналогичной задачи из 8 варианта, особенный интерес здесь представляет нахождение второго значения параметра a. Также отметим, что в сборнике в ответах допущена ошибка (не была произведена проверка принадлежности полуплоскости).

Задача. Найдите все значения a, при каждом из которых система неравенств

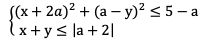
имеет единственное решение [2, с. 42].

1) a=5, O(-2a;a)=O(-10;5)

-10+5<|5+2|,  -5<7

т.е. при a=5 наша система имеет единственное решение.

Кроме рассмотренных случаев, можно составить задачу так, что ни при одном значении параметра a задача не будет иметь решения.