В курсе математики, значительную часть занимает материал по темам уравнения и неравенства. Самым сложным разделом, который изучается в школе, считается иррациональные уравнения, поскольку на их решение уделяется очень мало внимания. Обучающиеся достаточно часто допускают ошибки при решении иррациональных уравнение, так как недостаточно владеют умением решать их.
При изучении иррациональных уравнений возникают следующие трудности:
- отсутствие четкого алгоритма решения;
- неправильное преобразование;
- потеря корней.
Задачи на тему «Иррациональные уравнения» встречаются на проведение ОГЭ (Основного Государственного Экзамена) и при различных вступительных экзаменах, но неправильное решение данных номеров, часто для ребят является огромным препятствием на пути достижения поставленной цели.
Поэтому в данной статье, я решила, рассказать о различных методиках решения иррациональных уравнений и показатьприменение этих методик на примерах.
Для начала давайте разберемся, что же такое иррациональное уравнение и какой вид оно имеет. Иррациональным называется уравнение, которое содержит под знаком корня переменную. Примером иррационального уравнение будет являться:
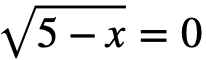
Существуют различные методики решения иррациональных уравнений, перечислим их:
- метод возведения обеих частей уравнения в одну и ту же степень;
- метод введения новых переменных;
- разложение на множители.
Разберем подробно каждый метод и приведем пример решения иррациональных уравнений каждым методом.
1 метод: метод возведения обеих частей уравнения в одну и ту же степень. Смысл его том, чтобы избавиться от корня и получить рациональное уравнение, которое более легко при решении.
Но нужно помнить, если обе части иррационального уравнения мы будем возводить в нечетную степень, одну и ту же, то у нас получится уравнение, которое равносильно данному. А если же мы возведем в четную степень, то получится уравнение, которое будет следствие данного, именно из-за этого возможно появление посторонних корней решения уравнений.
Рассмотрим пример использования метода возведения частей в одну и туже степень при решения иррационального уравнения.

Равенство получилось верным, поэтому данный корень будет являться корнем данного уравнения.
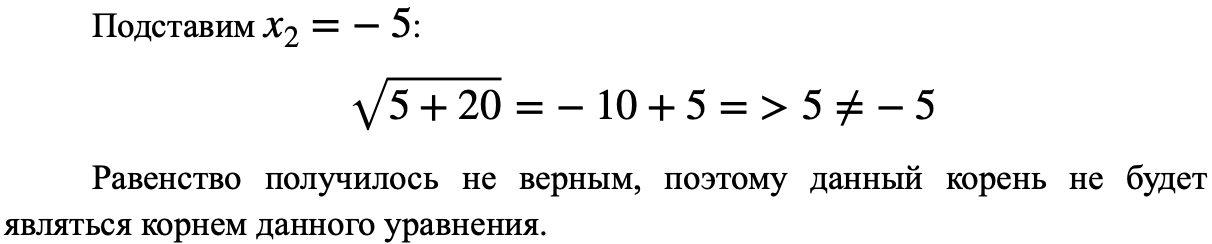



Равенство получилось верным, поэтому данный корень будет являться корнем данного уравнения.
Ответ: 1, 0, 3
В данной статье, я рассказала про методы решения иррациональных уравнений и показала примеры применения каждого метода. Каждый метод решения иррациональных уравнений по-своему интересен для обучающихся, но для каждого наиболее легкий метод решения свой. Кому-то легче возвести обе части в одну и ту же степень, кому-то же заменить переменной общий множитель. Но полагаясь на свою практику, хочется отметить, что всё-таки основным методом решения, у обучающихся, чаще всего является 1 метод, метод возведения обеих частей уравнения в одну и ту же степень.
Список литературы
- Мордкович, А. Г. Алгебра. 8 класс. – В 2 ч. – Ч. 1. Учебник для учащихся общеобразовательных учреждений. 12-е изд. [Текст] / А. Г. Мордкович – М. : Мнемозина, – 2010 – С. 215.
- Сканави, М. И. Сборник задач по математике для поступающих в вузы. 6-е изд. [Текст] / М. И. Сканави – М. : Наука, – 2013 – С. 608.



