В наше время технология вычислений является сильным инструментом для получения расчетов с большой точностью. Отсюда появился шанс обходиться от приближенных вычислений и производить их в точной форме. Полезное использование вычислительной техники невозможно представить без обдуманного применения приближенных способов и численных методов.
Цель определения корней уравнения находится во многих сферах науки и востребована в данный момент. Она неоднократно является фундаментальным началом при решении исследовательских и прикладных задач.
Способы численности направлены на решение вопросов, появляющихся в работе. Решение вопросов конкретными способами осуществляется за счет использования алгебраических и логических операций над числовыми компонентами, что разрешает полезно использовать ВТ. Из-за присутствия погрешностей формулировка и исследования вопросов являются неточными. Фактором их наличия является неверно выполненная математическая модель объекта реальности, ошибка данных в условии, неверный способ решения, ошибка округления.
Нахождение корней алгебраических уравнений является одним из самых популярных вопросов математического анализа, важность которого появляется в многоэтапных и самых разновидных отделах физической науки, механики и в других прикладных дисциплинах.
Этап нахождения корней заключается в том, что определяется примерное значение корня, который находится на интервале (a;b), с закрепленной погрешностью ℇ. Рассматривая данное понятие, необходимо ввести формулу:

В практических целях популярности достигли способы закрепления корней:
1.способ деления наполовину;
2.способ хорд;
3.способ касательных;
4.способ обычной интерпретации.
Исследуем алгоритм каждого способа с помощью математически-программной среды:
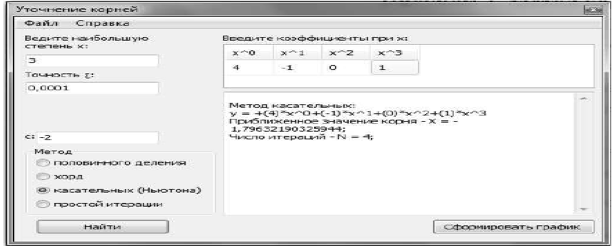
Рис.1- способ касательных
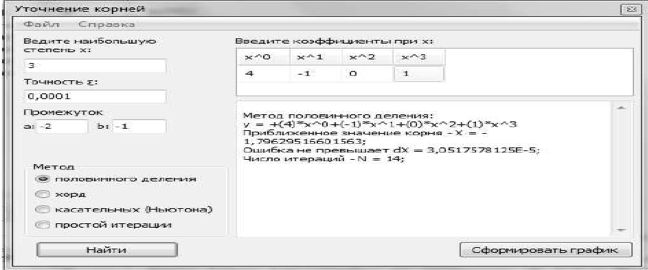
Рис.2- способ половинного деления
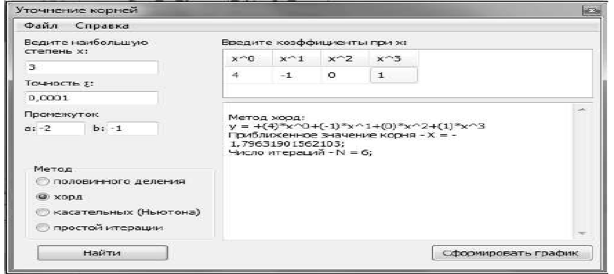
Рис.3- способ хорд
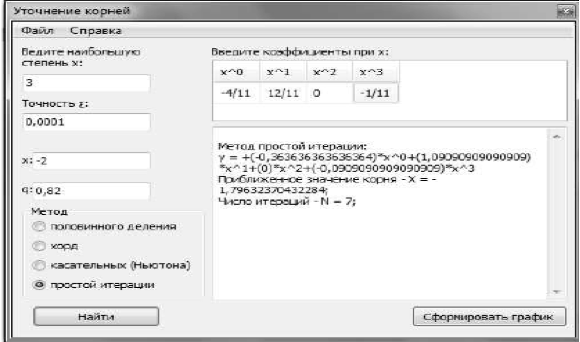
Рис.4- способ обычной интерпретации
Заключение:
Нахождение корней алгебраических уравнений, может иметь место не только в образовательных целях, но и в практической жизни. В деятельности будущих инженеров, механиков и других технических специалистов, умение правильно находить корни алгебраических уравнений является фундаментальной задачей.
Но для того чтобы избежать длительного решения, погрешностей результатов, созданы программные среды, которые обладают набором всех инструментов алгебры и прикладного анализа.
Список литературы
- Б.П. Демидович, И.А Марон. Основы вычислительной математики. - Москва, изд. «Наука»; 2010.
- В.М. Вержбицкий. Численные методы (линейная алгебра и нелинейные уравнения). - Москва, «Высшая школа»; 2000.
- .С. Бахвалов, А.В. Лапин, Е.В. Чижонков. Численные методы в задачах и упражнениях. - Москва, «Высшая школа»; 2009.
- Мэтьюз Джон, Г. Финк, Куртис Д. Численные методы MATLAB, 3-е издание. - Москва, «Вильяс»; 2010.



