РАЗНОСТНЫЙ МЕТОД АППРОКМИСАЦИИ КРАЕВОЙ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ТЕПЛОРОВОДНОСТИ ВТОРОГО ПОРЯДКА. МЕТОД ПРОГОНКИ

    Исследование процессов теплопроводности всегда играло важную роль в развитии технических и естественных наук. Самое интенсивное изучение данных процессов началось в конце девятнадцатого и в начале двадцатого веков из-за возрастающей потребности в теплоэнергетике. В течении следующих лет до наших дней появлялись новые задачи теплопроводности, которые выдвигали требования полноты и надежности - прогнозов теории. Теоретическое исследование процессов теплопроводности в настоящее время в значительной степени базируется на их математическом моделировании с использованием ЭВМ. Это стало возможным благодаря значительному прогрессу в развитии вычислительных методов решения задач для уравнений в частных производных и увеличению мощности современных вычислительных машин.  

     Большинство задач теплопроводности приводит к линейным и нелинейным дифференциальным уравнениям в частных производных, то есть уравнениям математической физики. Самым универсальным и весьма полезным является метод конечных разностей. По другому его называют методом сеток. Он дает возможность сводить приближенное решение уравнений в частных производных к решению систем алгебраических уравнений.

     В данной статье мы будем аппроксимировать первую краевую задачу обыкновенного дифференциального уравнения теплопроводности второго порядка. Запишем алгоритм решения разностной схемы методом прогонки.

    Поскольку мы будем рассматривать в данной статье лишь простейшую схему для уравнения теплопроводности второго порядка, то при решении разностной задачи используется лишь алгоритм одномерной прогонки.

 

   Запишем краевую задачу для уравнения теплопроводности:

 

                           (1)

 

   Для того чтобы составить разностную схему, приближенно описывающую данное дифференциальное уравнение, нужно сделать два шага:

1. Необходимо заменить область непрерывного изменения аргумента областью дискретного его изменения;
2. Необходимо заменить дифференциальный оператор некоторым разностным оператором, а также сформулировать разностный аналог для краевых условий и для начальных данных. [1]

 Выбрав одномерную сетку

 

и простейший трехточечный шаблон, получим разностную задачу

                   

                                                

                                                 или                                                                (2)

 

       

   Производим замену      в уравнение (2):

 

                                 (3)

 

с краевыми условиями

       .                                                (4)

 Здесь        – заданные числа.

    После составления разностной задачи, запишем алгоритм решения разностного уравнения.

    Будем искать решение уравнения в том же виде (2), в котором заданы краевые условия (3), т. е. в виде

                                         (5)

 

 где   и   – неизвестные пока коэффициенты

   Подставляя (5) и

                              

                               

 

а уравнение (3), получим

+ =0       (6)

 

   Отсюда видно, что уравнение (3) будет выполнено, если потребовать

 

=0,           +  =0.          (7)

 

  Тем самым мы получаем рекуррентные соотношения для определения прогоночных коэффициентов    и   :

 

 

       (8)

             

 

 Величины    и   находим из (5) краевого условия (4) при :

 

,  

 

  Значение , необходимое для начала счета по формулам (5), получаем из (5)  и краевого условия при :

 

 

                                                                 (9)

 

 

  Итак, мы можем получить точное решение краевой задачи (3) – (4) при помощи следующего алгоритма:

 

 

 

 

,                                                                                         (10)

,

 

 

 

   Перед решением надо проверить разностную схему на устойчивость. Прогоночные формулы (10) называются устойчивыми, если коэффициенты  αi  не превосходят по модулю единицу. В этом случае ошибки округления, возникающие в процессе счета по рекуррентной формуле (4), не будут возрастать.

 

    Выпишем условия устойчивости данной разностной схемы:

 

     Ai>0,         Bi>0 ,      Ci≥ Ai+Bi,     0≤ρα<1,    α =1, 2                   (10)   

 

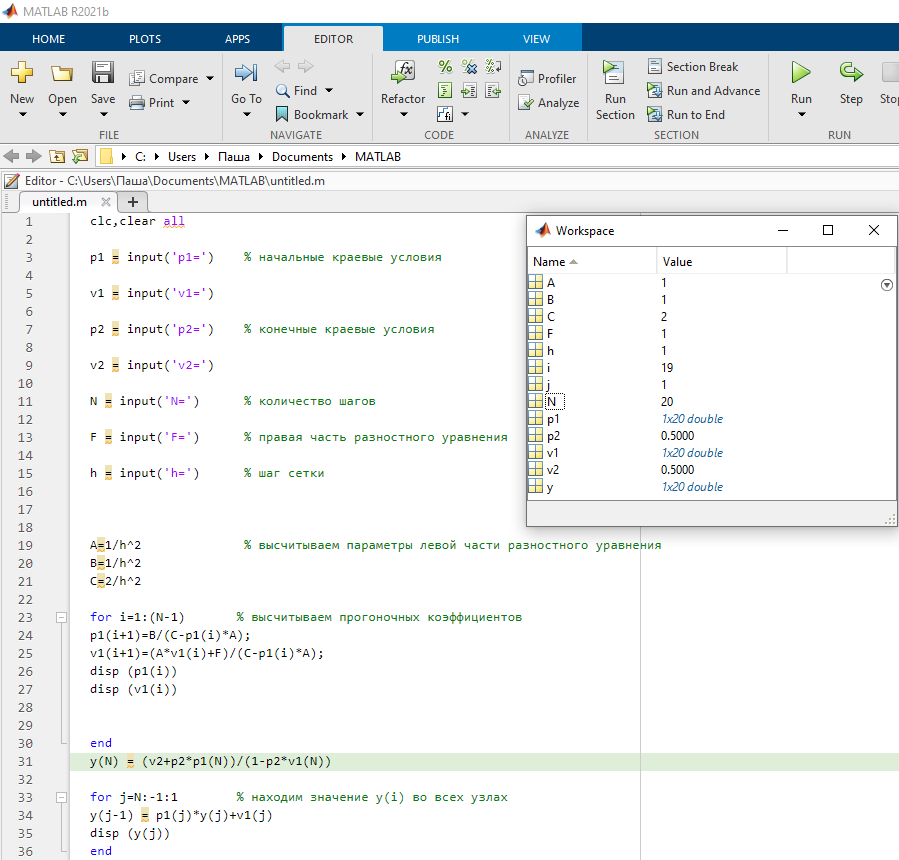
Рисунок 1-Алгоритм решения разностного уравнения методом прогонки на языке программы Mathlab

 

Рассмотрев алгоритм аппроксимации первой краевой задачи для обыкновенного дифференциального уравнения теплопроводности второго порядка с помощью прогоночного метода и алгоритм проверки разностной схемы на устойчивость, мы введём числовые значения параметров вместо латинских букв, чтобы наглядно показать решение данной задачи с помощью компьютерной программы Mathlab.

 

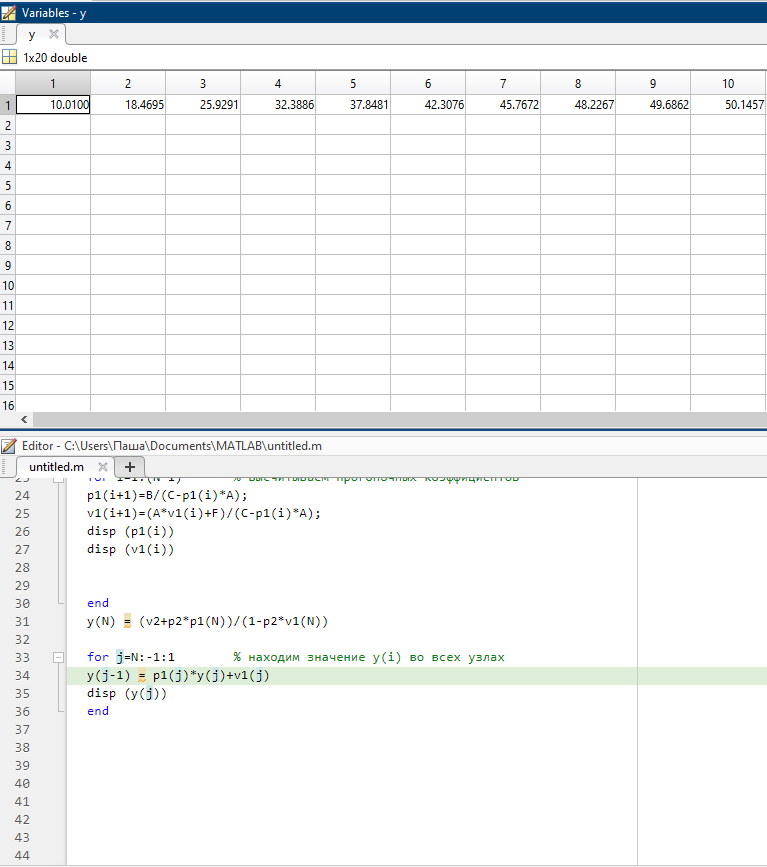
Рисунок 2-Полученные значения 

При анализе полученных значений   , мы можем сказать, что разность между полученных чисел    при каждом шаге уменьшается, следует, что разностная схема построена правильно, и она устойчивая.