НЕЛИНЕЙНАЯ ДИНАМИЧЕСКАЯ МОДЕЛЬ ВЗАИМОЗАВИСИМЫХ ОТРАСЛЕЙ ПРОИЗВОДСТВА

Качественный анализ динамической системы в первом приближении.

На данный момент существует множество статей и публикаций о нелинейных динамических системах (как пример, Нелинейная динамика взаимодействующих популяций [1]), но поскольку их анализ сложно подвести под общий случай, то в каждой статье имеется скорее некое количество частных случаев, чем общее решение. В данной работе будет разбираться один из таких частных случаев, а именно система двух взаимозависимых отраслей производства с учетом ферхюльстовских ограничений.

Существенным отличием от существующих работ (к примеру, от статьи: The nonlinear differential dynamics of interdependent branches of industry [2]) является именно наличие ограничений на продукцию, что существенно усложняет систему, но при этому приближает ее к реальной картине мира.

Целью данной работы является проведения качественного анализа динамической системы в первом приближении.

Для достижения приведенной выше цели были выполнены следующие задачи:

1. Найдены равновесные точки.
2. Определены типы устойчивости равновесных точек.
3. Проведен поиск точек бифуркации.
4. Построены фазовые портреты отдельных случаев.

Все вышеперечисленные задачи и методы их выполнения будут рассмотрены в данной работе. Но большая часть математических выкладок будет опущена, поскольку они будут скорее мешать, чем помогать разобраться в теме работы.

В работе будут рассмотрены две взаимозависимые отрасли производства: угольная и металлургическая промышленности (для угольной промышленности требуется металл, а для металлургической требуется энергия, в том числе и уголь).

                

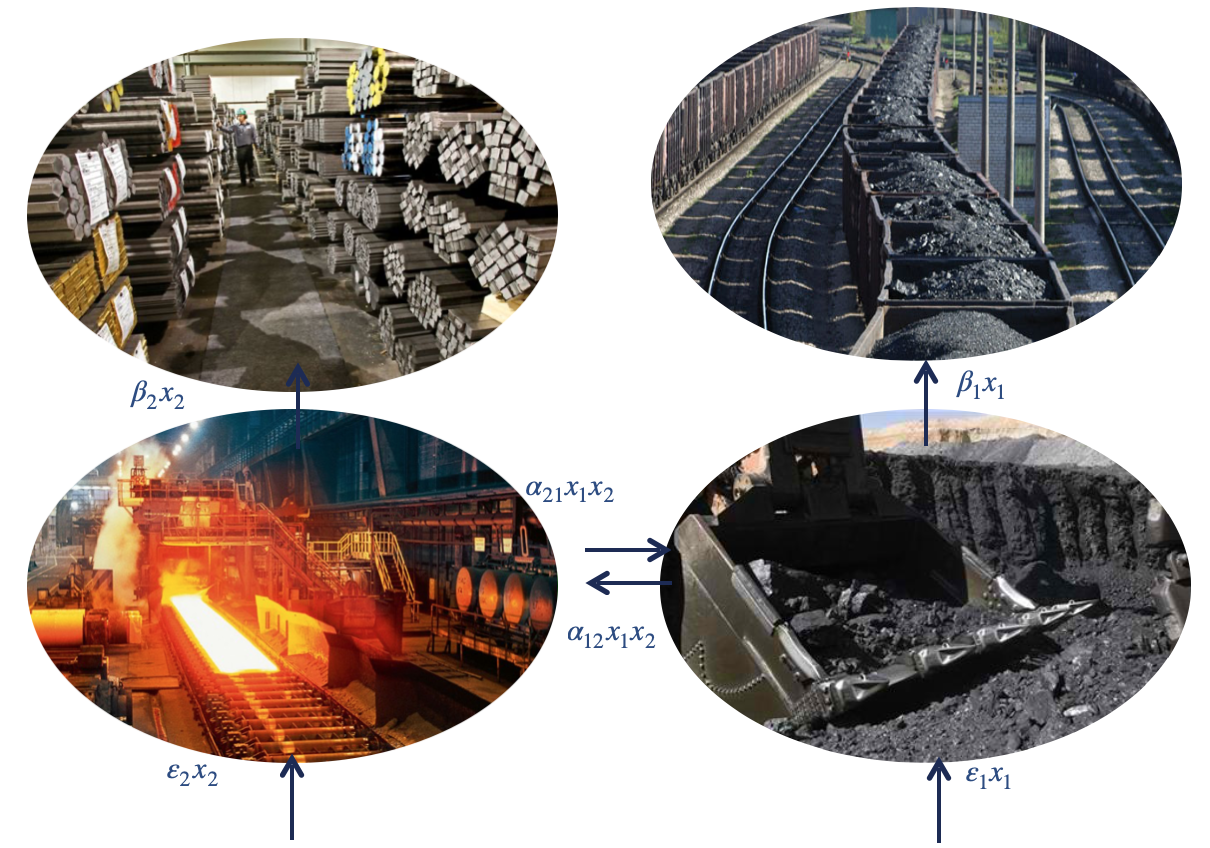
Рисунок 1. Зависимость отраслей производства

 

Таким образом, ориентируясь на описанный пример, отображённый на рисунке 1, получаем систему двух взаимозависимых отраслей производства с добавленными ферхюльстовскими ограничениями.

Исходная динамическая система:

                                                             (1)

Слагаемое означает рост количества продукта первой отрасли, не зависящий от второй отрасли с ферхюльстовским ограничением,

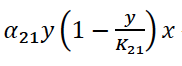— рост количества продукта первой отрасли, зависящий от количества продукта второй отрасли, с ферхюльстовским ограничением,

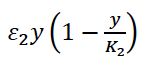— рост количества продукта второй отрасли, не зависящий от первой отрасли с ферхюльстовским ограничением,

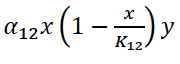— рост количества продукта второй отрасли, зависящий от количества продукта первой отрасли, с ферхюльстовским ограничением,

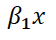  —рыночное потребление продукции первой отрасли,

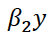  — рыночное потребление продукции второй отрасли,

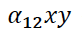  — потребление продукции первой отрасли (сырья) второй отраслью,

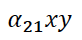  — потребление продукции второй отрасли (сырья) первой отраслью.

В этой системе все параметры положительные числа.

Введем некоторые обозначения, которые в некоторых случаях будем использовать в дальнейшем:

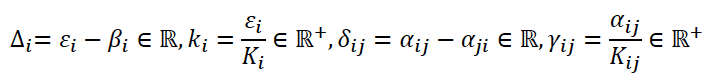
Для нахождения равновесных точек приравниваем оба уравнения к нулю.

Опустим математические вычисления. В итоге получим четыре возможных случая.

Случай 1: (x, y) -> (0,0). Хоть случай неинтересен с экономической точки зрения, но все же для качественного анализа он необходим.

Тогда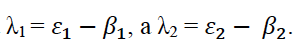 

В зависимости от значений параметров получаем несколько типов устойчивости.

Рисунок 2. Фазовые портреты случая 1 для λ₁ > 0, λ₂ > 0 и  λ₁ < 0, λ₂ > 0

 

λ₁ > 0 и λ₂ > 0 следовательно, неустойчивый узел.  λ₁ < 0 и λ₂ > 0 следовательно, седло. Фазовые портреты для данных значений параметров  изображены на рисунке 2.

 

Рисунок 3. Фазовые портреты случая 1 для λ₁ > 0, λ₂ < 0 и  λ₁ < 0, λ₂ < 0

 

λ₁ > 0 и λ₂ < 0 следовательно, седло. λ₁ < 0 и λ₂ < 0 следовательно, устойчивый узел. Фазовые портреты на рисунке 3.

Случай 2: (x, y) -> (0, .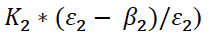

Поскольку мы рассматриваем неотрицательные значения x и y (с точки зрения реального взаимодействия производств они подразумеваются не отрицательными), то .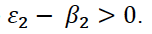

Тогда λ₁ =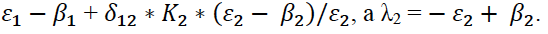  

Заметим, что λ₂ неположительное. Таким образом, тип устойчивости зависит лишь от λ₁.

Если λ₁ > 0, то седло. Если λ₁ < 0, то устойчивый узел.

 

Рисунок 4. Фазовые портреты случая 2 для λ₁ > 0 и λ₁ < 0

 

Для фазовых портретов на рисунке 4 были заданы такие параметры, что равновесная точка — точка (0, 1).

Случай 3: (x, y) ->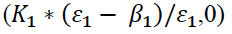

Поскольку мы рассматриваем неотрицательные значения x и y, то .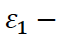

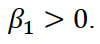Тогда λ₁ =

Заметим, что λ₁ неположительное. Таким образом, тип устойчивости зависит лишь от λ₂.

Если λ₂ > 0, то седло.

Если λ₂ < 0, то устойчивый узел.

В данном случае получаем фазовые портреты аналогичные случаю 2, отображённых на рисунке 4.

Случай 4. Самый интересный с экономической точки зрения случай, а также сложнейший с математической точки зрения, когда переменные не равны нулю, а строго положительны.

В этом случае найти равновесную точку не так просто, как в предыдущих случаях, поскольку предстоит работать со степенными функциями, от которых раньше мы избавлялись.

Если не вдаваться в подробности вычислений, то решая стандартным способом получили бы следующие равновесные точки:

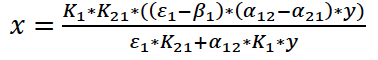                                                                    (2)

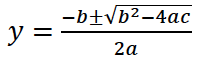                                                                              (3)

где

b =  ,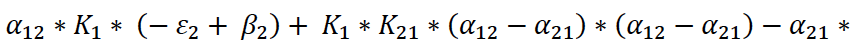

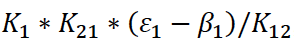a = ,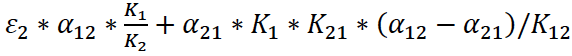

c = .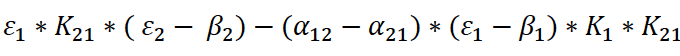

Если подставить все сокращения в выражения для равновесных точек, то очевидно, что оно будет слишком большим и не удобным для дальнейшей работы. К тому же, после этого для определения типа устойчивости нам понадобится якобиан и его собственные значения. Даже определив несколько условий, к примеру, что переменные положительны, получится слишком сложное для определения знака собственных значений выражения (как пример, в Wolfram Alpha выражение для каждого собственного значения заняло более 5 строк). Таким образом, так просто проверить все возможные варианты не получится.

Исходя из всего вышесказанного было решено построить взаимное расположение нуль-изоклин, а после построить фазовые портреты для определённых параметров. Таким образом, не придется делать сложных вычислений, и станет возможным определить тип устойчивости по фазовым портретам.

Уравнения нуль-изоклин нашей системы после некоторых математических выкладок имеют следующий вид:

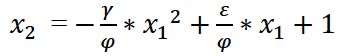                                                                    (4)

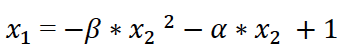                                                                   (5),

где

 

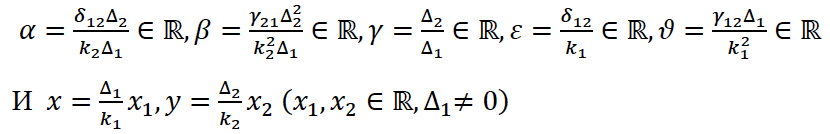
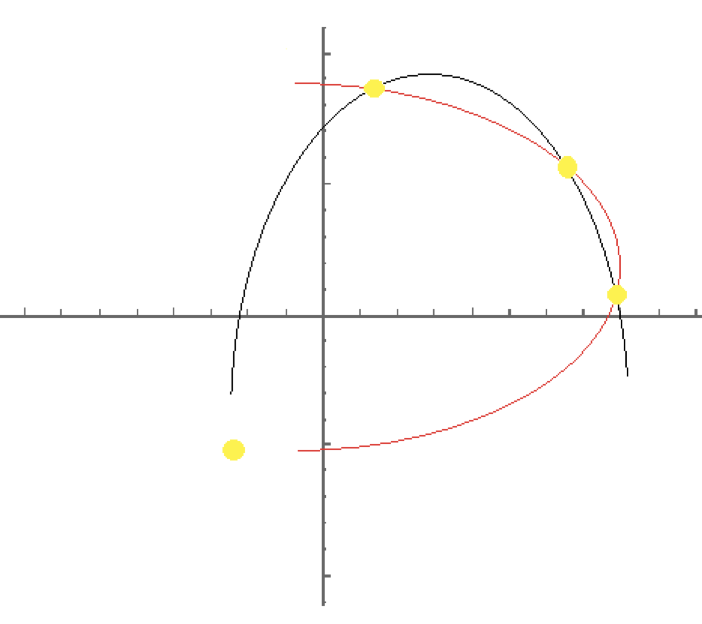
Рисунок 5. Расположение нуль-изоклин

 

На рисунке 5 представлен один из возможных случаев расположения нуль-изоклин. Всего возможно 4 случая:

1. 4 общие точки (представлен на рисунке 5)
2. 3 общие точки
3. 2 общие точки
4. 1 общая точка (параболы касаются друг друга)

В зависимости от случая будет происходить изменение портрета системы.

Для примера рассмотрим случай 1. Тогда для четырех общих точек достаточно, чтобы значение функции 4 в вершине было больше, чем положительный корень уравнения 5, когда оно равно нулю, и аналогично значение функции уравнения 5 в вершине должно быть больше, чем положительный корень уравнения 4, когда оно равно нулю.

 

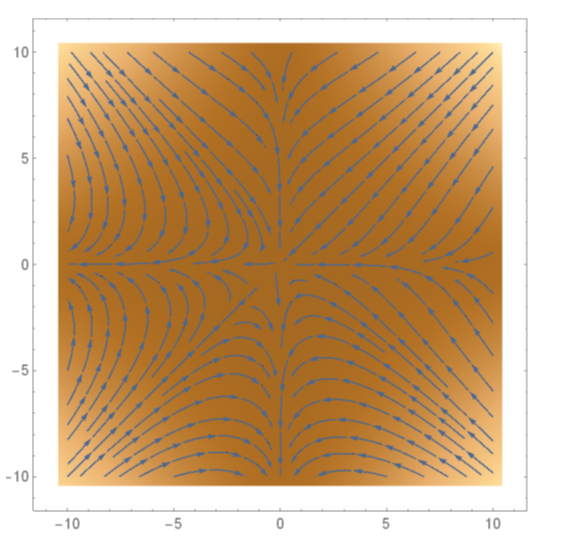
Рисунок 6. Плотностная диаграмма потоков

 

На рисунке 6 отображена плотностная диаграмма потоков для данного случая, и стоит отметить, что как оказалось фазовый портрет со схожими параметрами уже рассматривался ранее.

Таким образом, пользуясь методом нуль-изоклин, можно построить фазовые портреты для каждого отдельного случая и провести анализ основываясь только на нем, не вычисляя равновесные точки, которые в общем случае вычислить напрямую становится куда сложнее.