Введение
Воздушный транспорт является важным средством перемещения в современном мире. Восходящий и нисходящий потоки являются очень опасными погодными явлениями для воздушного судна. В данной статье мы рассмотрим дифференциальное уравнение горизонтального полета, зависимость коэффициента подъёмной силы от коэффициента лобового сопротивления. А также как данные явления могут повлиять на аэродинамику воздушного судна в полете.
Задачи
- Проанализировать дифференциальное уравнение горизонтального полёта без учёта влияния восходящего воздушного потока
- Построить график зависимости Cy от Cx при горизонтальном полёте и траекторию движения воздушного судна
- Рассмотреть учёт влияния восходящего воздушного потока на лётные характеристики воздушного судна, проанализировать изменение дифференциального уравнения горизонтального полёта.
- Построить график зависимости Cy от Cx при горизонтальном полёте и траекторию движения воздушного судна с учётом влияния восходящего воздушного потока.
Дифференциальное уравнение горизонтального полёта
Движение самолёта описывается векторным уравнением вида:
Для получения дифференциальных уравнений горизонтального полёта в скалярном виде спроектируем векторы входящие в уравнения на оси траекторной системы координат:
Первое уравнение характеризует изменение скорости прямолинейного горизонтального полёта под действием разности сил: тяги силовой установки и силы лобового сопротивления.
При установившемся горизонтальном полёте считается, что 
, следовательно уравнения принимают вид:
Уравнение расчёта подъёмной силы имеет вид: 
Уравнение расчёта силы лобового сопротивления имеет вид: 
График зависимости Cy от Cx и график траектории полёта воздушного судна
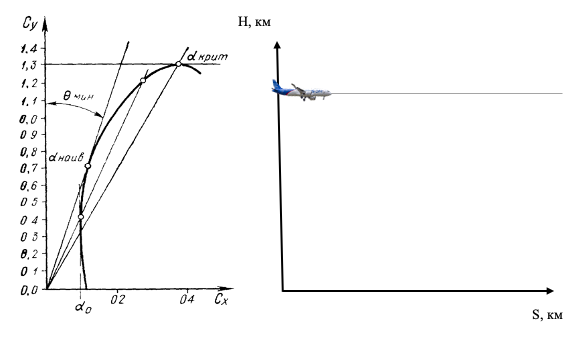
Влияние восходящего потока на уравнение движения воздушного судна
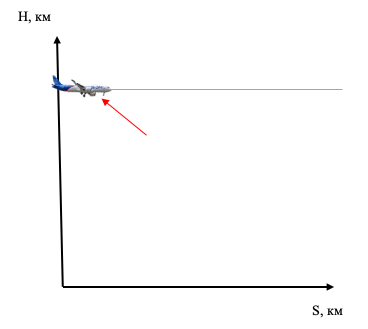
Пусть восходящий поток имеет направление, показанное красной стрелочкой, и скорость равную U, тогда проекция этой скорости на вертикальную ось будет равна 
, где α – угол, под которым направлен восходящий поток к продольной оси воздушного судна.
Таким образом, с учётом влияния восходящего потока уравнения подъёмной силы и силы лобового сопротивления примут вид:
Так как под влиянием восходящего потока подъёмная сила стала численно больше силы тяжести, а сила лобового сопротивления стала больше тяги силовой установки, то уравнения, используемые для установившегося горизонтального полёта, не справедливы для данного случая. Соответственно:
Из этого следует, что дифференциальное уравнение неустановившегося горизонтального полёта под действием восходящего потока воздуха будет иметь вид:
При условии, что G=const.
Подставим в получившееся уравнение уравнения подъёмной силы и силы лобового сопротивления с учётом влияния восходящего воздушного потока:
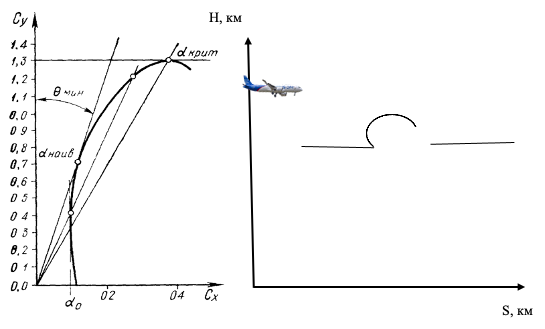
Из данного уравнения мы можем сделать вывод, что при воздействии восходящего потока воздуха на воздушное судно появляется дополнительная составляющая силы лобового, которая создаётся из-за скоростного добавка к скорости основного воздушного потока, что приводит к замедлению воздушного судна. Отсюда можно сделать вывод, что при воздействии восходящего воздушного потока, направленного под углом α против направления движения самолёта, появляется дефицит тяги, поэтому нужно увеличить режим работы двигателей. Также мы видим, что появилась составляющая подъёмной силы из-за воздействия восходящего потока воздуха, что приводит в взмыванию самолёта, то есть отклонению от заданной траектории, а соответственно к потере скорости и дефициту тяги. Чтобы преодолеть данное возмущение тоже требуется добавить режим работы двигателей.
Таким образом попадание в восходящий воздушный поток, направленный под углом α против направления движения самолёта влечёт за собой серьёзную потерю скорости и отклонение от намеченной траектории движения, что сказывается не только на лётных характеристиках воздушного судна, но и на расходе топлива, затрате времени на полёт, а также на безопасность полёта.
График зависимости Cy от Cx и график траектории полёта воздушного судна с учётом влияния восходящего воздушного потока
Список литературы
- Аэродинамика и динамика полета, Николаев Л.Ф.
- Высшая математика. Дифференциальные уравнения, Аскар Туганбаев
- Электронный учебно-методический комплекс «Высшая математика »,Е.А. Ровба, Е.А. Сетько, А.С. Ляликов, К.А. Смотрицкий
- Динамика полета. Расчет летно-технических и пилотажных характеристик самолета, Кривель С.М.
