МАТЕМАТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ БАЛЛЬНО-РЕЙТИНГОВОЙ СИСТЕМЫ НА ПРИМЕРЕ ФУТБОЛЬНЫХ КЛУБОВ ВЫСШЕЙ ЛИГИ

Введение

Футбол в мире традиционно является самым популярным видом спорта.

Впервые правила игры в футбол были введены 7 декабря 1863 года Футбольной ассоциацией Англии. Основывались они на придуманных в Кембриджском университете положениях игры.

С каждым годом индустрии футбола уделяется все больше внимания. В докладе рассматривается схема построения системы рейтингования субъектов футбола, предложены группы факторов, изложены общие принципы рейтинговой оценки и целевые результаты, которых подобная система позволит достичь. В настоящее время правила устанавливает Международный совет футбольных ассоциаций (IFAB). Именно этот орган инициировал введение в футбол автоматической системы рейтингов.

Давайте разберемся и узнаем, что такое балльно-рейтинговая система в футболе.  Данная система – это система ранжирования футбольных клубов и сборных. Каждые из них отличаются различными критериями подсчета.

А что же из себя представляет сам рейтинг? Рейтинг - индивидуальный числовой показатель (коэффициент) достижений команды, меняющийся в зависимости от его результатов в соревнованиях.

Для чего они нужны и как оно нам помогает? Благодаря данной системе, мы можем объективно оценивать силу футбольной команды на данный момент и в данном промежутке времени; также мы можем прогнозировать исход любого матча, и знать какая команда является фаворитом или аутсайдером в взятом нами матче( что является наиболее важной вещью для болельщиков и букмекеров (им это надо для составления коэффициентов для ставок)

Существует много факторов для сборных и клубов, которые необходимы для составления рейтинговой системы. Например, важность матча.

Количество очков в рейтинге зависит от результатов игр команды, силы соперников и важности матчей. За каждый сыгранный матч командам прибавляются или вычитаются очки согласно правилам.

Рассмотрим основы формирования балльно-рейтинговой системы на примере футбольных клубов высшей лиги, где лига включает в себя несколько чемпионатов и кубков.

Основные факторы и положения

Система рейтингования может быть построена по следующей схеме:

1. Присвоение каждому чемпионату/кубку коэффициент сложности(важности)
2. Расчет формулы для ожидаемого результата

2.1 Присвоение командам максимальный потолок очков

3. Составление системы присвоения очков в зависимости от исхода мата
4. Присвоение дополнительных очков за матч в гостях и за победу в финале
5. Создание конечной формулы для нахождения полученных баллов за матч
6. Нахождение тенденции за определенный промежуток времени
7. Присвоение класса команде

С данной системой мы сможем рассчитывать баллы команд по окончанию чемпионата, а также в любом туре чемпионата, кубка и т.п.

1.1 В высшей футбольной лиге существует множество различных чемпионатов, с разной сложностью и важностью. Относительная важность игры играет огромную роль при формировании рейтингов и вывода формулы для расчета очков за какой-либо проведенный матч. Так, например, товарищеская игра или контрольный матч имеют значительно меньшую важность, чем игра в финале Лиги Чемпионов (это самый престижный кубок). Для удобства придумали систему коэффициентов, повышение которых зависит от престижа и сложности чемпионата. Рассмотрим некоторые из них в таб.1

Таб.1

Название чемпионата/вида матча	Коэффициент
Контрольные матчи (неофициальные)	0
Товарищеские матчи	0.5
Матчи с определенным регламентом, но не имеющие веса	1
РПЛ (Россия)	1.1
УПЛ (Украина)	1.09
Матч группового этапа Лиги Европы	1.7
Матч группового этапа Лиги Чемпионов	1.8
Плей-офф Лиги Европы/Чемпионов	2.0/2.1
Финал Лиги Европы/Чемпионов	3.0/3.5

 

Как мы видим сложность разных чемпионатов отличается. Обозначим коэффициент статуса как “S”

1.2 Для создания формулы счета очков нам необходимо создать формулу для ожидаемого исхода матча (также благодаря этому мы можем предсказывать вероятный исход матча). В моей системе, по правилам, новая команда попадает в высшую лигу с 4000 очками (это будет стартовый баланс очков).

Теперь составим систему оценки очков за исход любого матча:

• Победа – 2 очка
• Ничья – 1 очко
• Поражение – 0 очков

Создадим скелет для формулы исхода матча [E]:

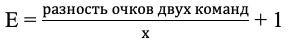
Мы видим, что у нас есть неизвестная Х, которая нам не позволяет считать. Нам требуется ее найти. Величина Е должна лежать в промежутке (0;2), так как количество очков за исход не может быть больше или меньше 2 и 0 соответственно, а так же равняться 2 или 0,так как ,при допущении, что ожидаемый исход равен  2 или 0, выходит так что слабая команда не имеет никакого шанса на победу, что по теории вероятности невозможно.

2.2.1 Дальше мы сталкиваемся с проблемой “разности очков”. В теории данная величина может быть сколь угодно большой или малой, и из-за этого мы не сможем высчитать постоянную величину Х. Поэтому мы введем такое понятие как “потолок очков”, данная величина показывает максимально возможное кол-во очков команды. В нашей системе максимально количество возможных очков равно 20 000, а минимально 0 очков.

Теперь составим систему для нахождения Х с наибольшей и наименьшей разностью очков:

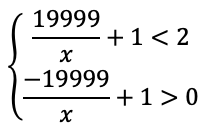
Решая данную систему, мы получаем результат

х ∈ (-∞;0)∪(19999;+∞)

Отрицательные числа мы не берем т.к. наши уравнения теряют логический смысл. И поэтому мы возьмем наименьшее натуральное число из возможных. Это 20000

Запишем теперь итоговую формулу для расчета ожидаемого результата матча

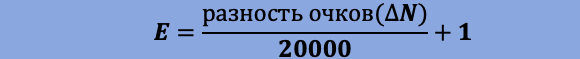
1.3 Раз у нас уже есть готовая формула для вычисления ожидаемого исхода матча, то нам не сложно будет составить часть формулы, где присутствуют очки за исход матча.

Очевидно, что у сильной команды шансов на победу больше, и ее победа более ожидаема. Но бывают случаи, когда аутсайдер сенсационно обыгрывает фаворита. И давать одинаковое количество очков за победу и аутсайдеру, и фавориту будет несправедливо, тк один обыграл сильного с меньшим шансом на победу, а другой “закономерно” выиграл. И при проигрыше такая же ситуация: поражение фаворита должно отнимать больше очков, чем поражение аутсайдера.

Для этого можно сделать линейную функцию с ожидаемым исходом (W) и полученным исходом (которую мы в дальнейшем вставим в конечную формулу для подсчета очков за матч)

I = W – E

1.4 Очевидно, что команде намного легче играть на домашнем стадионе, чем в гостях. Ведь дома они привыкли к своему газону, их поддерживает армия болельщиков и самое главное – им не нужно тратить силы на перелет и тп. Поэтому нужно как-то поощрять игры в гостях. Для этого введем коэффициент A. Он будет зависеть от того как далеко надо ехать команде на матч с соперником (игры в финале на нейтральном стадионе учитываться не будут)

 

Таб.2

Зависимость коэффициента A
Игра дома	0
Игра в гостях в пределах страны	0.1
Игра в другой стране в той же части света	0.15
Игра в другой части света	0.2

 

За победу в финале очки только за победу умножаются на 1.5.

1.5 В предыдущих пунктах были получены отдельные коэффициенты и формулы, необходимые для формулы очков после матча.

Составим формулу получаемых баллов после матча:

Так как команда имеет какое-то кол-во баллов до матча (N), то величину Q мы будем прибавлять к имеющимся баллам

И теперь составим конечную формулу рейтинга команды после матча:

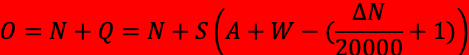
По данной формуле мы с легкостью сможем определить очки команды после какого-либо матча и сможем составлять динамические рейтинги за определенный промежуток времени

Также для нахождения формы команды за определенное кол-во матчей можно использовать данную формулу: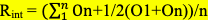 

Если R_int положительно, то значит график очков команды движется вверх, и команда набирает форму, если отрицателен – наоборот.

1.6 Спустя огромное количество матчей мы сможем столкнуться с тем, что команды доходят до потолка баллов, и дальше просто не могут развиваться в рейтинге. Поэтому эту проблему можно решать добавлением рейтингу динамичности. Чтобы добавить рейтингу динамичности мы будем смотреть на выступления команды в ближайшие 200 матчей, то есть 4 года (50 матчей в год в среднем). Полученные баллы за прошлые матчи мы будем отнимать. Но если мы будем их просто отнимать, то мы просто будем забывать их былые заслуги, поэтому мы будем оставлять 20% этих баллов

 

1.7 Для удобства нахождения команды в рейтинге, и понятия в какой она форме на данный момент мы создадим отдельные классы команд. Для их создания мы воспользуемся различными интервалами в рейтинге.

1. 0-3000 – низкий уровень
2. 3001-7000 – удовлетворительный уровень
3. 7001-11000 – достаточный уровень
4. 11001-15000 – высокий уровень
5. 15001+ – очень высокий уровень  

 

Пример небольшой таблицы команд

Возьмем для примера расчета возможных полученных очков в зависимости от исхода матча 4 команды с разным рейтингом:

1. Реал (Мадрид) – 16472 балла
2. Зенит (СПб) – 11249 баллов
3. Динамо (Киев) – 8315 баллов
4. Спартак (Москва) – 7857 баллов

Построим таблицу получаемых баллов от возможных исходов матчей на основании данных рейтингов

Таб.3

Динамо

Зенит

Спартак

Реал

Динамо

Матч плей-офф ЛЧ, дома

Товарищеский матч, в гостях

Матч финала ЛЧ

+2.4

+0.3

-1.7

+0.56

+0.06

-0.44

+7.38

В финале ничья невоз- можна

-2.07

Зенит

Матч плей-офф ЛЧ, в гостях

Матч РПЛ, дома

Матч группы ЛЕ, дома

+2.1

+0.006

-2.09

+0.9

-0.19

-1.28

+2.14

+0.44

-1.25

Спартак

Товарищеский матч, дома

Матч РПЛ, в гостях

Финал ЛЕ

+0.5

+0.01

-0.48

+1.28

+0.19

-0.9

+6.43

В финале ничья невоз- можна

-1.7

Реал

Финал ЛЧ

Матч группы ЛЕ, в гостях

Финал ЛЕ

+3.1

В финале ничья невоз- можна

-4.92

+1.26

-0.44

-2.14

+2.56

В финале ничья невоз- можна

-4.3

 

Пусть все команды выиграли все свои первые матчи (по горизонтали) и проиграли вторые матчи (по вертикали). Составим рейтинг после этих матчей:

1. Реал Мадрид – 16473.9
2. Зенит Санкт-Петербург - 11249.4
3. Динамо Киев – 8317.9
4. Спартак Москва – 7859.2

У слабых команд рейтинг при одинаковом количестве побед и поражений увеличился больше, чем у сильных. Это говорит о том, что рейтинг слабых команд более динамичен, чем у сильных.

Вывод

Рассмотрев вышеприведенную таблицу, мы можем проанализировать различные исходы, а также сделать выводы относительно данной системы рейтингов. Поражения сильных команд наказываются намного сильнее, чем слабых, ведь их победа ожидалась намного больше, но они сенсационно проиграли. В свою очередь победы слабых команд над сильными будут поощряться сильнее.

Также мы можем заметить, что ничья фаворита в своей лиге (где команды примерно равны) отрицательно сказывается на рейтинге (матч Зенит-Спартак).

В финале с аутсайдером сильным командам не стоит проигрывать, они теряют очень много баллов даже больше, чем теоретическая победа по модулю, хотя победа в финале имеет дополнительный коэффициент.

Иногда случаются матчи, когда обеим командам выгодно сыграть вничью. Например, матчи Динамо Киев – Спартак, Динамо – Зенит, при ничейном счете обе команды получают + в баллах, хоть он и не большой. Играть такие игры вничью особенно выгодно под конец чемпионата, когда команды не теряют место в рейтинге. Из-за этого у букмекеров на ничью будет повышенная вероятность на ничью в подобных матчах.

В общем, мы можем сделать вывод, что данная бально-рейтинговая система полностью отражает силу команды в любой момент (по R_int), а также показывает силу команды на более длительном промежутке. Мы с легкостью сможем понимать какая команда сильнее и предугадывать исход матча.

Дополнение

На подобии данной схемы, можно сделать бально-рейтинговую систему в авиации. Такую систему удобно использовать, как для целых авиакомпаний, так и для отдельных пилотов. Каждый пилот будет зарабатывать или же терять баллы после каждого полета. Например, за посадку будет три возможных исхода, как в футболе, 3 балла – отлично 2 балла – нормально, 1 балл – удовлетворительно. Коэффициенты будут зависеть от расположения аэропорта, покрытия ВПП, состояния воздушного судна и т.п. Также благодаря такой системе легче будет внедрять в рабочий процесс новое поколение пилотов. Курсант, только что закончивший обучение и стажировку, будет иметь маленький рейтинг, поэтому к нему посадят КВС с большим рейтингом, чтобы обеспечить хорошую безопасность полета и одновременно дать опыт молодому пилоту.

Буквенные обозначения

S – коэффициент статуса матча

N – рейтинг команды

А – гостевой бонус

n – количество матчей