ОТКРЫТИЕ НОВОГО КЛАССА ФУНКЦИЙ С УНИКАЛЬНЫМИ СВОЙСТВАМИ: ФУНКЦИИ-НЕВИДИМКИ ГУРО

Введение

Каждый школьник, студент, ученый знает понятия о числовых элементарных функциях и графиках. Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике – функции полезности, издержек, функции спроса, предложения и потребления, в радиотехнике – функции управления и функции отклика, в статистике – функции распределения.

Но если изобрести и попробовать сложить особым образом две или более простые элементарные функции, то можно прийти к открытию в математике!

У функций много свойств, но автор еще нашел свойство, о котором говориться в статье.

Перечислим основные свойства числовой функции:

возрастающая, убывающая;

ограниченная снизу, ограниченная сверху;

ограниченная слева, ограниченная справа;

наименьшее значение, наибольшее значение;

понятие выпуклой, вогнутой;

понятие непрерывной, дискретной,

понятие явной заданной, не явной заданной, понятие параметрической заданной.

А теперь добавим в этот список новое понятие – невидимые функции.

1. Открытие 11 февраля 2020 года

При сложении, например, двух корней или логарифмов с разными под функциями знаками получим то, о чем говориться в названии статьи. Напишем простую сумму двух логарифмов:

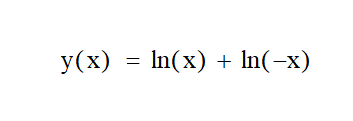
Аналитическую и простую формулу y(x) невозможно увидеть или изобразить или представить на графике на всей оси х. Все так просто можно придумать новый вид функций! Сумма элементарных функций может дать не изображаемую функцию.

              

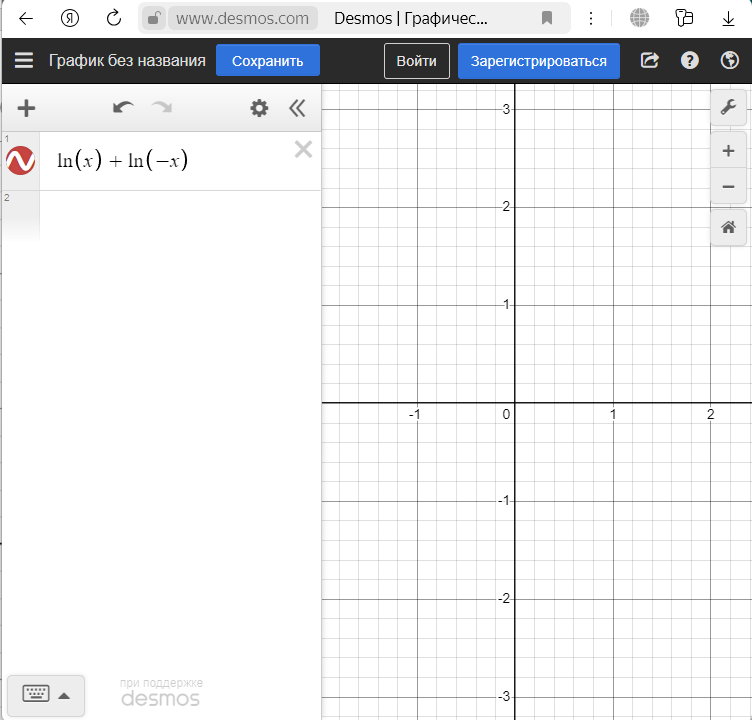
График 1. Попытка онлайн увидеть и нарисовать график невидимки

 

 

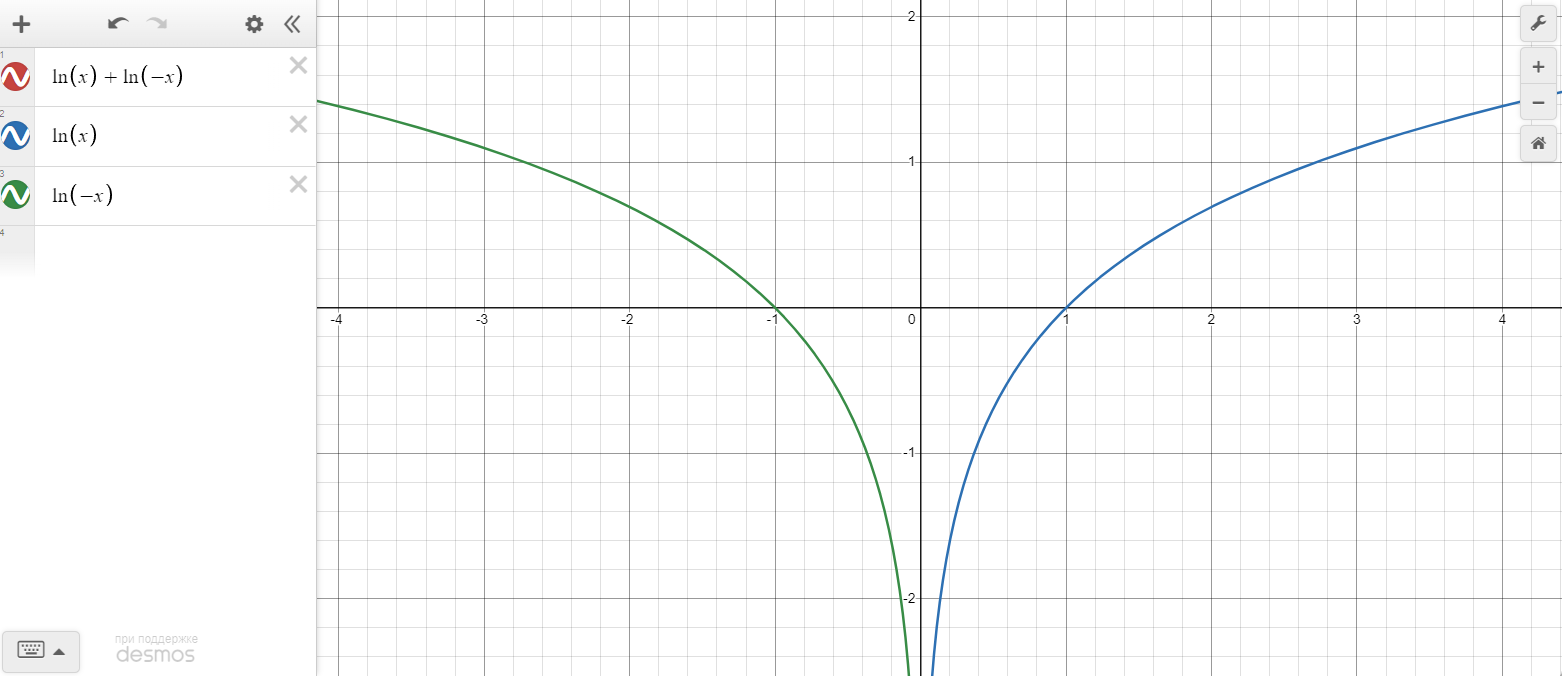
График 2. Видимые части графиков, составляющих функцию

И только для слагаемых, составляющих функцию можно график построить: Синяя линия –  положительная часть функции, Зеленая линия – отрицательная часть функции.

Назовем все варианты непрерывных или дискретных и любые комбинации аналогичных типа функций " НЕ ИЗОБРАЖАЕМЫЕ графически в декартовых координатах числовые функции» или просто "функции - невидимки " или "λειτουργία αόρατος ".

ПЕРВОЕ СВОЙСТВО: Важное свойство этих новых функций (производных или интегралов) заключается в том, что их нельзя графически на плоскости или трехмерном изменении представить — это нереально как представить в чистом виде 4D.

Под 4D понимается четырехмерное декартово пространство с началом координат, без вымышленных координат времени и всяких тессеракт или декеракт, и гиперкубов, вращающихся во времени и прочих странных умозрительных идей.

Можно утверждать, что НЕ ИЗОБРАЖАЕМОСТЬ (αόρατος) — это есть переход функций от вещественных к мнимым.

Так как у этих функций в простом случае Х всегда вещественный, а Y всегда мнимый.

Тогда логично придётся пересмотреть и добавить определение обычных функции (не комплексных!):

Функ­ци­ей на­зы­ва­ет­ся закон, по ко­то­ро­му каж­до­му эле­мен­ту Х ста­вит­ся в со­от­вет­ствие един­ствен­ный эле­мент Y, который может быть невидим на графике и не вычисляться в вещественном измерении.

Существует везде вещественный X, но нигде на графике не изображаем в вещественных числах Y, ответ вычисляется только в комплексном виде.

Особо важно заметить связь функции- невидимки с числом ПИ.

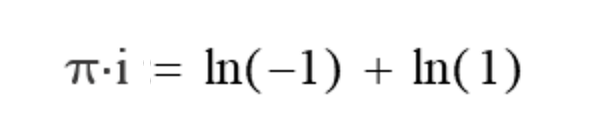
2. Новые законы и красота математики в функциях невидимках

Примечательно, что при вычислении невидимок для любых вещественных Х мнимая часть результата равна числу ПИ. Эта формула аналогична по смыслу тождеству, которое давно известно математикам 250 лет назад. Тождество Эйлера – это частный случай формулы Эйлера при x = π. Оно связывает пять фундаментальных математических констант:

e — число е, или основание натурального логарифма;

i — мнимая единица;

π — пи, отношение длины окружности к длине её диаметра;

1 — единица, нейтральный элемент по операции умножения;

0 — ноль, нейтральный элемент по операции сложения.

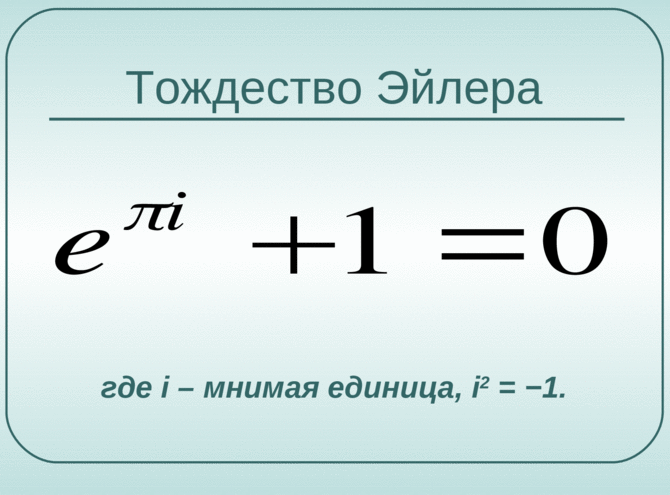
Рисунок 1. Тождество Эйлера

ЭТО тождество считается образцом математической красоты, поскольку показывает глубокую связь между самыми фундаментальными числами в математике.

Если Х будет только МНИМЫМ, то результат ВЕЩЕСТВЕННЫЙ:

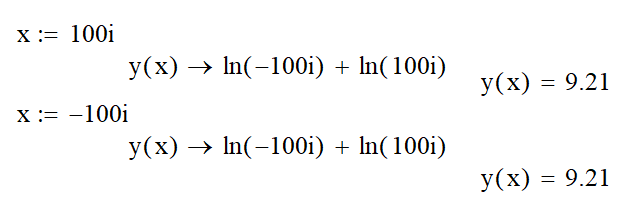
Если Х будет КОМПЛЕКСНЫМ, то результат КОМПЛЕКСНЫЙ:

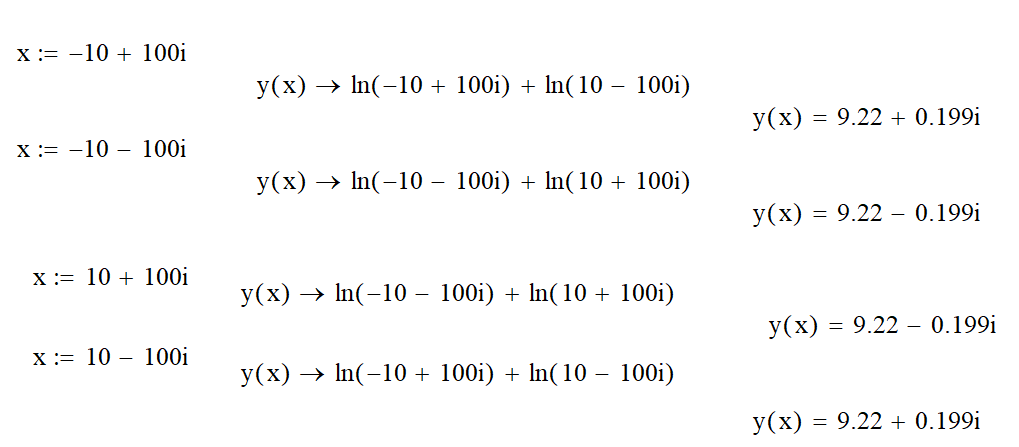
3. Интегралы и производные функции-невидимки

Существуют и изображаемы все производные функции невидимки:

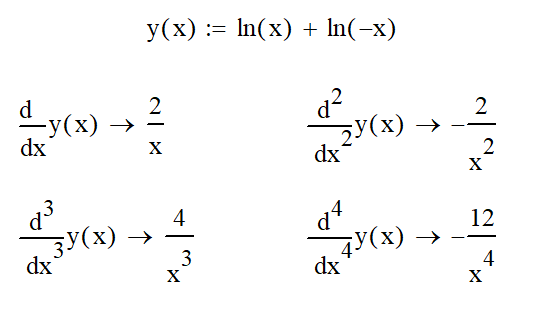
Теперь обратно проинтегрируем первую производную, и видно, что интеграл производной функции не равен изначальной функции невидимке:

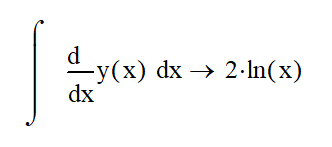
ВТОРОЕ свойство: если не изображаемую функцию продифференцировать и потом обратно проинтегрировать, то бывает итоговый ответ не равен исходному; или: интеграл производной функции может быть не равен функции.

Интегралы тоже существуют в записи аналитической, любых уровней интегрирования – но они также не изображаемы:

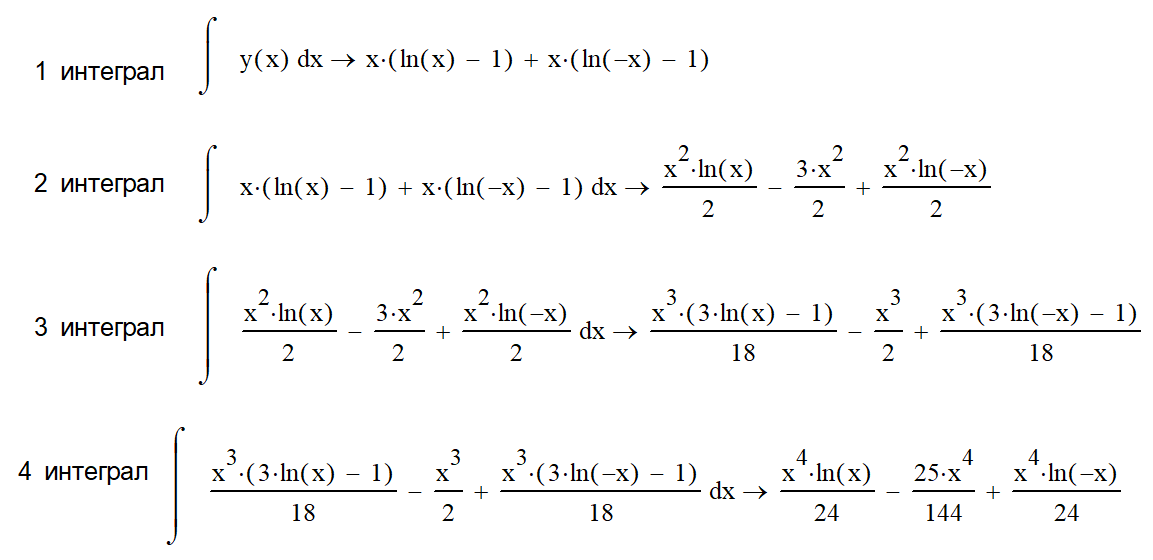
ТРЕТЬЕ свойство: не изображаемые интегралы не изображаемых функций- невидимок рекуррентны или фрактальны.

3. Семейство всех функций-невидимок

Если введем разные масштабные по осям слагаемых и разные сдвиговые параметры для функции, то при x*K1+B1>0 и -x*K2+B2<0, то получим семейство КРИВЫХ не изображаемой функции при различных параметрах:

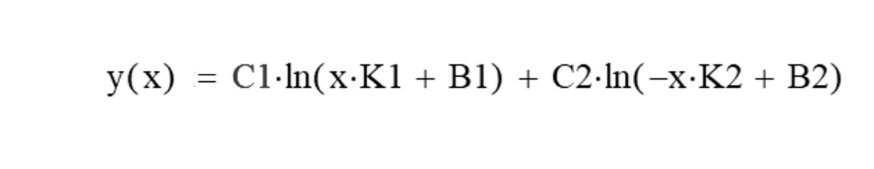
Производные функции невидимки первая, вторая и третья в общем виде:

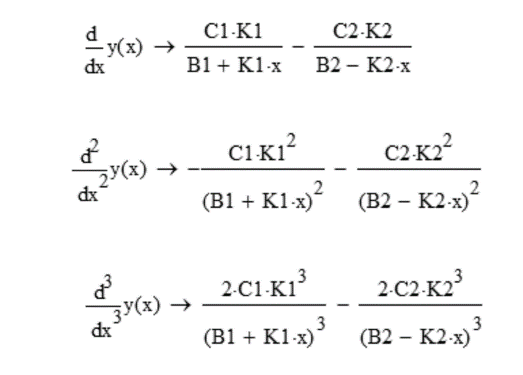
в общем виде первый интеграл тоже не изображаемый.

         

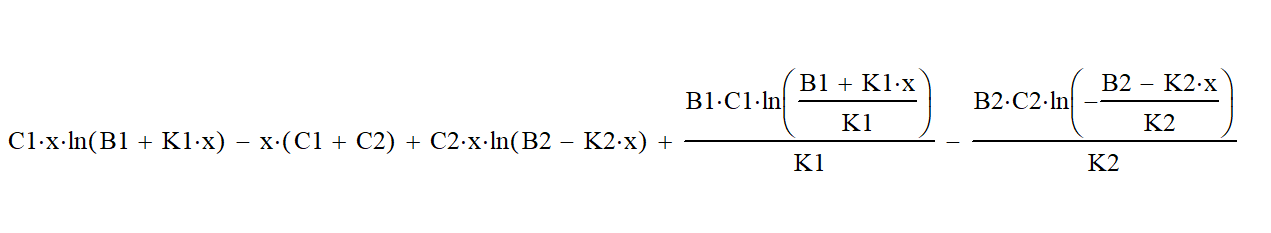
Второй и высшие интегралы в общем виде не могут уместиться в габариты левой и правой стороны статьи, так как очень длинные формулы получаются.

Четвертое свойство: у функций-невидимок бывают и видимые производные, которые можно изобразить на графике.

Второе свойство функций-невидимок сохраняется и в общем виде, и сначала берем производную и обратно интегрируем, и опять интеграл производной функции не равен функции.

Можно считать функцию-невидимку отображением мнимым - зазеркальем, производную-зеркалом, интеграл не равный функции – человеком, который смотрит в зеркало и не узнает себя вообще....

4. Обобщение на любые действия

Если составные части не изображаемой функции умножить или вычесть или разделить или возвести в степень или рекуррентно вычислять саму себя и иные смешанные действия, и операции добавить:

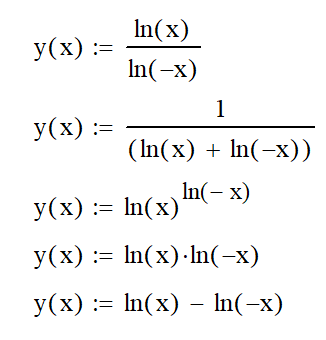
то получим сложную, но все равно не ИЗОБРАЖАЕМУЮ функцию, со своими новыми и необычными свойствами:

5. Примеры других не изображаемых функций

1) не изображаемый корень y(x)= x^0.5+(-x) ^0.5

у функции "не изображаемый корень" есть одна видимая особая точка x=y=0 т.е. график- невидимка с одной точкой видимой, но уж совсем странно и интересно.

2) Фрактально вложенная N раз сама в себя не изображаемая функция

y1(x)=ln(x)+ln(-x) базовый фрактал, y2=ln( y1 )+ln(- y1 ),  y3=ln( y2 )+ln(- y2 ),

yN=ln( y(N-1) )+ln(- y(N-1) ) построения N фрактала для второго y2 (и прочих вложений) входной Х2 равен функции Y1, которая невидима сама!

Получаем невидимый фрактал, который нельзя отобразить на всех уровнях!

3) Составим дифференциальные уравнения с функцией невидимки

y(x)'=ln( y(x) )+ln(- y(x) )     или    y(x)=ln( y(x)' )+ln(- y(x)' )     

и хотим найти решение дифф уравнения первого порядка.

Или второго порядка y(x)"=ln(y(x)’) +ln (- y(x)’)

Как решить такое?  Решением будет явно Комплекснозначная функция!

И может ли быть решением обычного дифференциального уравнения комплексные числа, при вещественном Х?

Так просто аналитически не решить, а обычные численные методы расчета решения дифференциальных уравнений не рассчитаны на комплексные числа.

Вывод

Автор кратко исследовал на практике (Маткад 15) новые функции-невидимки, и читателем предлагает при желании самостоятельно выявить другие свойства функций-невидимок и сделать новые открытия. После этого можно будет применять в различных математических прикладных науках, с получением небывалых ранее результатов.

В ходе глубокого и всестороннего исследования функций-невидимок, можно открыть и найти еще новые тайны математики, о которых со времен сотворения мира, еще никто из людей не узнал, а всё что мы знаем и имеем сегодня – это капля в море или ноль в сравнении с бесконечностью. Поэтому был прав Сократ, сказав: «Я знаю, что я ничего не знаю".