Метод рационализации, как один из методов решения неравенств, известен уже около 50 лет. В разных источниках названия данного метода разнятся. Названия – метод декомпозиции, метод замены множителей, обобщенный метод интервалов, подразумевают под собой один и тот же метод [4].
Решение нестандартных неравенств сопряжено со многими техническими сложностями, что чревато как логическими, так и вычислительными ошибками. Применение стандартных способов решения неравенств часто бывает затруднительным или невозможным. Метод рационализации позволяет избежать многих нежелательных осложнений и ускорить процесс решения неравенств.
Из свойств рационализации можно получить высказывание позволяющие эффективно сводить сложные иррациональные, степенные и трансцендентные неравенства к рациональным неравенствам, поэтому в литературе говорят о методе рационализации.
Мнение авторов по поводу происхождения названия метода рационализации разнятся, одни считают, что название происходит от сведения неравенств к рациональным неравенствам (А.Г. Корянов, А.А. Прокофьев), другие же отталкиваются от возможности более рационального решения неравенств (В.В. Мендель) [3].
Сам термин «рационализация неравенств» впервые встречается в работах Г.В. Дорофеева, в 1969 году, а идея метода декомпозиции (но без названия) встречается у В.П. Моденова в 1972 году, в 2001 году автор уже даёт ему название. Так же иногда в литературе используется термин «метод замены множителей», эта терминология берет своё начало в 90-х годах [1].
Метод рационализации (метод декомпозиции, метод замены множителей, метод замены функций, правило знаков) заключается в замене сложного выражения F(x) на более простое выражение G(x), при котором неравенство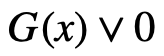 
равносильно неравенству 
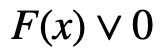в области определения выражения F(x) [2].
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G, где f, g, h - выражения с переменной x, a - фиксированное число (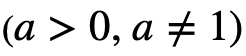
. И представим свойства метода рационализации в виде таблицы 1 [5].
Таблица 1. Свойства метода рационализации
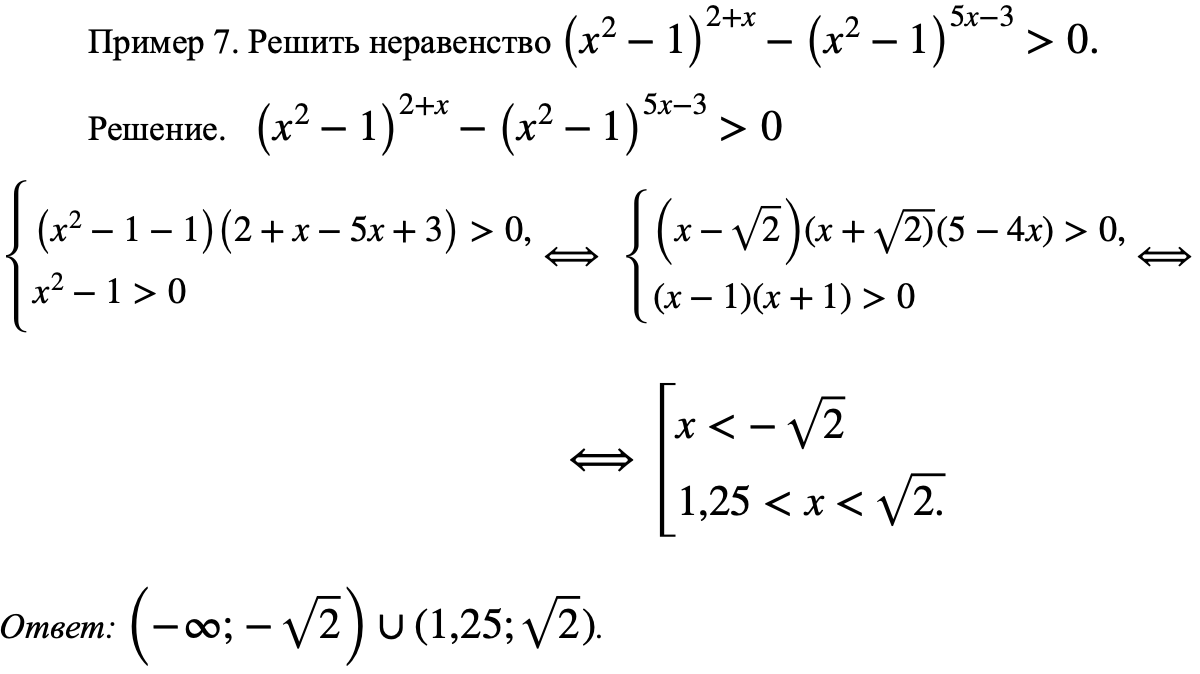
Метод рационализации упрощает решение, позволяет достаточно просто рационализировать многие иррациональные неравенства, неравенства с модулем, логарифмические и показательные неравенства с постоянным и переменным основанием, а также сложные комбинированные неравенства.
Список литературы
- Дорофеев Г. В. Обобщение метода интервалов / Дорофеев Г. В. // Математика в школе. – 1969. - № 3. С. 39-44.
- Коропец З.Л. Нестандартные методы решения неравенств и их систем / Коропец З.Л., Коропец А.А., Алексеева Т.А. // Математика. – 2012. 125 с.
- Корянов А. Г., Методы решения неравенств с одной переменной [Электронный ресурс] / А. Г. Корянов, А. А. Прокофьев. – URL: https://alexlarin.net/ege/2011/C3-2011.pdf
- Моденов В. П. Метод декомпозиции при решении трансцендентных неравенств / В.П. Моденом // Математика в школе. – 2001. – № 5. С. 64-68
- Фазлеева Э.И. О применении метода рационализации при решении неравенств. – URL: https://kpfu.ru/staff_files/F1977879220/Metod_racionalizacii.pdf
