ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ДЛЯ РАСЧЕТА ОСНОВНЫХ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ УСТРОЙСТВ

Современная теория и расчет показателей надежности и долговечности строятся в значительной мере на использовании законов, положений математической статистики и теории вероятности, которая привлекается для анализа практически полученных отказов машин. Вероятностный характер отказов объясняется их стохастичностью, большой степенью неопределенности появления во времени, их зависимостью от большого, трудно учитываемого числа факторов и условий эксплуатации машин. В подавляющем большинстве случаев отказ является случайным событием [1].

Закономерности появления случайных событий достаточно хорошо разработаны. Теорема о равенстве единицы суммы вероятностей двух противоположных событий гласит:

P(t)+Q(t)=1                                                                                  (1)

где    P(t) — вероятность безотказной работы изделия за время t;

         Q(t) — вероятность появления отказа за время t.

Отсюда P(t) =1 - Q(t),   т. е.   P(t)<1 всегда.

В структурном отношении по надежности перегрузочные машины относятся к изделиям с последовательным соединением элементов, когда отказ любого из них приводит к отказу всей машины, установки, комплекса.

На основе теоремы умножения вероятностей таких событий по каждому элементу вероятность безотказной работы такой системы представится произведением:

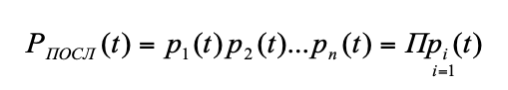                                                               (2)

где 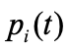— вероятность безотказной работы і-го элемента установки в течение времени t;

п — общее число последовательных элементов, влияющих на отказ всей технической или технологической цепи (системы).

Из формулы (2) видно, что вероятность безотказной работы установки значительно уменьшается с ростом числа последовательно составляющих ее элементов и всегда меньше безотказной работы каждого из элементов.

При параллельном соединении элементов (при резервировании) отказ одного из них не приводит к отказу всей установки. Здесь можно рассчитывать вероятность отказа установки как произведение:

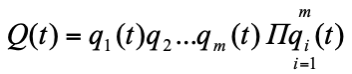                                                                (3)

где 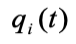 — вероятность отказа i-гоэлемента установки за время t;

т— число параллельно соединенных элементов.

Учитывая  (1)  и 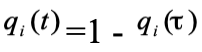, можно, преобразуя  (2),  написать:

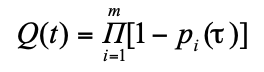                                                                       (4)

Отсюда вероятность безотказной работы установки с параллельным соединением элементов:         

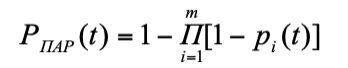                                                           (5)

Эта формула показывает, что вероятность безотказной работы установки с параллельным соединением элементов всегда выше вероятностей безотказной работы составляющих ее элементов.

Сравнительно часто встречаются и смешанные системы соединений, например у портального крана «Сокол» два параллельно действующих механизма вращения, каждый из них имеет последовательно соединенные детали и узлы. Этому отвечают и двухдвигательные приводы лебедок и других машин [2].

Вероятность безотказной работы смешанной системы, имеющей параллельные цепи, которые состоят из п последовательно соединенных элементов, можно найти из уравнения (5), заменив вероятность безотказной работы одного элемента p_i(t) вероятностью безотказной работы цепи Р_ц(t). Тогда

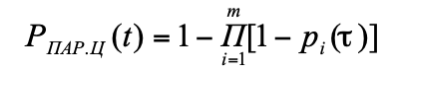                                                       (6)

Выразив: 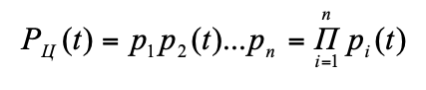                                                                                                                  (7)

подставим это значение в формулу  (6)  и получим:

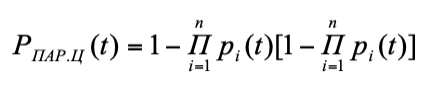                                                         (8)

Надо учитывать, что не каждая конструкция с параллельно работающими механизмами или узлами может рассматриваться как структурная (по надежности) схема с параллельным соединением элементов. Например, при отказе одной из параллельных цепей двухгусеничного хода   крана  или двухреечного    привода механизма вылета стрелы портального крана «Ганц» и др. отказывает вся система. Такие установки относятся к системам с последовательным соединением элементов. Для гусеничного хода безотказность определяется по формуле:

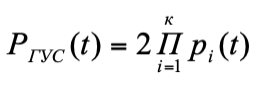                                                                           (9)

где к— число последовательных деталей гусеницы.

Изделия разделяют на неремонтируемые, или заменяемые после первого отказа, и ремонтируемые, которые могут иметь более чем один отказ.

Критериями предельного состояния деталей, узлов машин, когда невозможна или недопустимо мала эффективность их эксплуатации, являются: отказ (для неремонтируемых изделий), повышение интенсивности отказов или нарушение требований техники безопасности, наступление периода морального устарения. При этом учитывается возможность отказа машин и вследствие их хранения (хранение — одна из фаз эксплуатации техники).

Основными показателями надежности технических устройств, которые в процессе эксплуатации могут находиться только в двух состояниях - работоспособном и неработоспособном, являются следующие:

- вероятность безотказной работы за время;

- вероятность безотказного хранения за время;

- средняя наработка до первого отказа;

- условная средняя наработка до  первого отказа;

- среднее время безотказного хранения;

- условное среднее время безотказного  хранения;

- среднее время восстановления и  время техобслужанивания;

- ресурс (измеритель выбирается при нормировании показателей   надежности);

- ресурс при хранении;

- срок службы;

- среднее значение параметра потока отказов за ресурс;

- наработка на отказ;

-коэффициенты готовности, технического использования и оперативной готовности.

Показатели надежности технических устройств при хранении принимаются, когда устройство хранится до  отказа; и   когда устройство   хранится до отказа   или  до  предельного состояния.

Величина условной средней наработки до первого отказа есть средняя наработка до первого отказа элементов, эксплуатация которых прекращается после истечения установленного ресурса. Часто наработка, указанная в технической документации, значительно больше ресурса, когда элемент, проработавший ресурс, заменяется на новый. Таким образом, наработка до первого отказа характеризует условную надежность элемента, которая определяется по формуле:

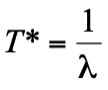                                                                                      (10)

где 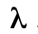  — интенсивность отказов для периода нормальной эксплуатации.

В качестве показателей ремонтопригодности наряду с временным показателем могут использоваться показатели трудоемкости и материалоемкости.

Показатели надежности компонентов, используемых в основных изделиях различного назначения, должны содержать максимальную информацию об их надежности [3].

Для изделий с постоянной интенсивностью отказов должны указываться лямбда-характеристика 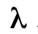(интенсивность отказов) в период нормальной эксплуатации и ресурс (или 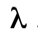— срок службы). Для изделий с переменной интенсивностью отказов должны указываться или вероятность безотказной работы для установленного порядка длительной работы, или вероятность безотказной работы для такого же ряда и ресурс (или срок службы).         

Может также использоваться для компонентов лямбда-характеристика в отдельные периоды эксплуатации (ее среднее, максимальное или минимальное значения).

В результате изложенного можно сформулировать общий порядок выбора показателей надежности:                                     

• Устанавливаются критерии отказа и предельного состояния. Выбор критерия производится в следующем порядке:

- устанавливают перечень параметров и допустимые пределы их изменения исходя из требований потребителя и условий эксплуатации с учетом достигнутого уровня науки и техники;

- с учетом требований потребителя и их технической выполнимости устанавливают перечень технических параметров, которые определяют  работоспособность   изделия;

- для технических параметров, определяющих работоспособность, устанавливают величины допусков, выход за пределы которых означает отказ. Эти допуски записывают в нормативно-техническую документацию на изделия как критерий их отказов.

• Определяется предельное состояние изделия. Критериями предельного состояния являются невозможностью его дальнейшей эксплуатации или недопустимым снижением эффективности.
• Устанавливается шифр изделия.  При этом первая цифра шифра   (подкласс  изделия)   устанавливает, ремонтируемое    или   неремонтируемое изделие; вторая — критерий  ограничения   продолжительности   эксплуатации;     третья — временной    режим   использования; четвертая — доминирующий фактор  при оценке  последствий отказа.

Факт выполнения или невыполнения изделием заданных ему функций в определенном объеме рассматривается как доминирующий, когда использование изделия связано с выполнением конкретного задания.

Факт вынужденного простоя может рассматриваться как доминирующий в тех случаях, когда при оценке последствий, вызванных отказом, определяющую роль играет вынужденный простой изделия, а величина ущерба пропорциональна длительности простоя.

Факт отказа может быть доминирующим в том случае, когда наличие отказа не приводит к невыполнению какой-либо конкретной задачи, вызванной отказом.

• Рассчитываются значения показателей надежности. В основу принципа оценки надежности может быть положена общая оценка функционирования изделия, в качестве которой принимается общий экономический эффект от использования машины (изделия).