РАСЧЕТ ЭКОНОМИЧЕСКОЙ НЕЭФФЕКТИВНОСТИ МАРШРУТА ПОЛЕТА ВС

Воздушные перевозки - это сложная система, зависящая от множества факторов. Вот как два основных фактора, такие как неблагоприятные погодные условия и загруженность трассы, могут влиять на экономическую неэффективность воздушного маршрута:

1. Неблагоприятные погодные условия:

• Неблагоприятные погодные условия, такие как туман, грозы, сильные ветры и снегопады, могут привести к задержкам и переносу полетов, что увеличивает операционные издержки и снижает эффективность маршрутов.
• Планирование маршрутов должно учитывать вероятность неблагоприятных погодных условий на каждом участке и возможность альтернативных маршрутов или пересмотра расписания.

2. Загруженность трассы:

• Загруженность воздушного пространства может привести к увеличению времени полета из-за необходимости ухода от других воздушных судов или ограничений в контролируемых воздушных областях. Это может повысить расход топлива и увеличить время в пути.
• Планирование маршрутов должно учитывать загруженность трассы и возможность выбора менее загруженных маршрутов или оптимального времени вылета.

Рассмотрим вопрос расчета экономической неэффективности маршрута самолета с учетом двух вышеперечисленных факторов, включая вероятность неблагоприятных метеорологических условий на маршруте и загруженность маршрута, и предоставим подход к оценке и оптимизации маршрутов, который основывается на использовании функций, учитывающих вышеперечисленные факторы.

Для описания причин, которые влияют на экономическую неэффективность маршрута полета ВС, можно использовать функцию, которая учитывает погодные условия и загруженность маршрута.

Тогда функция, описывающая экономическую неэффективность маршрута полета ВС, может быть представлена функцией двух переменных:

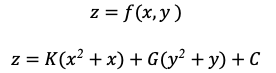
Чем больше значение данной функции, тем менее эффективен выбранный маршрут полета.

Функция погодных условий зависит от дальности участка маршрута:

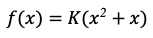
Квадратичная зависимость: Функция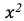вносит вклад дальности участка маршрута в погодные условия, который увеличивается нелинейно с ростом дальности из-за того, что погодные факторы могут изменяться нелинейно по мере продвижения по маршруту. Например, с увеличением дальности могут возникать новые метеорологические условия или интенсивность существующих условий может изменяться. В свою очередь, добавление члена x вносит вклад дальности участка маршрута в погодные условия. Например, средняя температура или влажность воздуха может изменяться пропорционально дальности.

Член 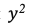в уравнении указывает на то, что увеличение числа самолетов приводит к нелинейному росту загруженности. Это связано с тем, что с увеличением количества самолетов возрастает количество возможных взаимодействий между ними, что повышает уровень загруженности. Добавление члена y учитывает линейный вклад каждого отдельного самолета в загруженность воздушного пространства. Это связано с тем, что каждый самолет вносит некоторый базовый уровень загруженности, который добавляется к общей загрузке.

где G - коэффициент времени года (летом больше, чем зим.)

G=1 в самом загруженном по пассажиропотоку месяце. По статистическим данным по перевозкам авиакомпании определяется соотношение пассажиропотока в текущем месяце к максимально загруженному месяцу, и коэффициент G выражается в долях от максимума.

Также необходимо учесть корректировочное значение С=const, которое учитывает вклад непредвиденных погодных явлений и перекрытие воздушных трасс.

Тогда конечный вид функции будет выглядеть так:

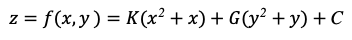
Задача - найти минимум данной функции. Построить график и объяснить на основе функции, в каком случае маршрут будет наивыгоднейшим.

Воспользуемся функцией для решения конкретного примера: Необходимо оптимизировать маршрут Москва-Сочи (при каких условиях полет будет наивыгоднейшим для авиакомпании) на основе данных о загруженности воздушного пространства и метеорологических данных. Для расчетов взять месяц Январь. Коэффициент С принять равным за 0,5.

Решение: Как было установлено выше, экономическая неэффективность маршрута полета является функцией 2-ух переменных: погодные условия и загруженность воздушного пространства z=f(x,y). Рассмотрим каждую переменную по отдельности.

Функция погодных условий выражается формулой:

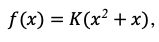
Рассматривается 2024 год, суммарно у нас 31 дней, из них 15 пасмурных, из которых 11 с грозой.

Функция загруженности воздушного пространства выражается формулой:

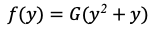
По статистическим данным на январь приходится околопиковая загрузка по пассажиропотоку в связи с выгодным географическим расположением обоих городов, большим населением и календарными праздниками, поэтому по данным авиакомпании G=0,9. Получим функцию:

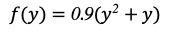
Таким образом, функция экономической неэффективности примет вид:

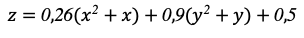
Найдем точку глобального минимума, где экономическая неэффективность будет минимальной.

Получим:

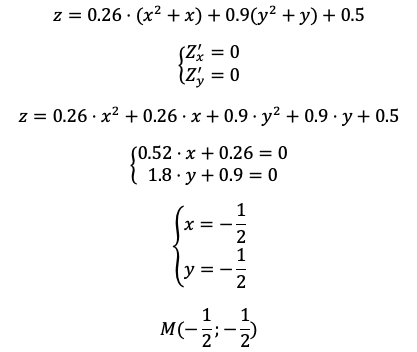
Достаточные условия

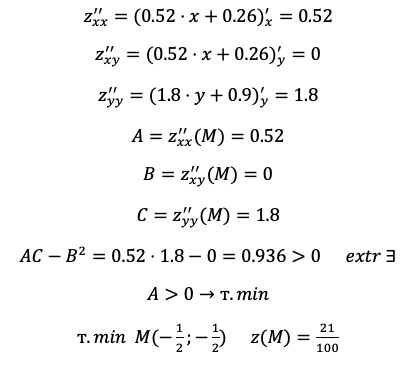
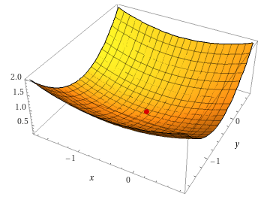
Рисунок 1. График функции нескольких переменных, в условиях данной задачи

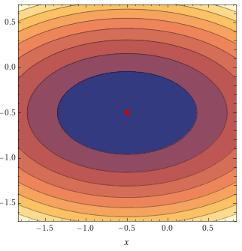
Рисунок 2. Контурный график функции нескольких переменных, в условиях данной задачи

В данной работе был проанализирован вопрос расчета экономической неэффективности воздушных маршрутов с учетом факторов, таких как неблагоприятные погодные условия и загруженность трассы и наличие запретных зон.

Основные выводы включают в себя следующее:

• Неблагоприятные погодные условия могут существенно увеличить операционные издержки и время полета. Учет вероятности неблагоприятных погодных условий на маршруте помогает минимизировать риски и обеспечить безопасность полетов.
• Загруженность трассы и наличие запретных зон также влияют на экономическую эффективность маршрутов. Планирование маршрутов должно учитывать эти ограничения и находить оптимальные решения.