Когда-то давно, еще в середине 17-го века такие ученые как Блез Паскаль, Пьер Ферма и Христиан Гюйгенс играли в азартные игры, поэтому они анализировали исходы игры и возможность выигрыша. Тогда они обратили внимание, что абсолютно случайные события имеют некую закономерность, которая в свою очередь зависит от количества так называемых испытаний. [1]
Теория вероятности – это математическая наука, которая изучает возможность появления положительного или отрицательного характера исходов в тех или иных испытаниях. [2]
Как нам известно, из жизненного опыта, многие события случайны. Под случайными событиями понимаются те явления, которые никто не в силах предугадать. Вероятность – это возможность появления случайного события в определенном испытании, поэтому, чем больше мера вероятности события, тем больше шансов на его наступление.
В рассматриваемой математической науке часто встречается стандартная формула по нахождению вероятности случайных событий:
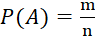 , (1)
, (1)
где:
Р – вероятность;
А – конкретное событие;
m – число всевозможных вариаций происхождения опыта;
n – количество благоприятных исходов. [3]
В зависимости от поставленной математической задачи, выделяют следующие группы событий:
1) Событие называется достоверным, если оно обязательно наступит. Если событие точно не свершится в результате конкретного опыта, его называют невозможным. К примеру, во время подбрасывания кубика из шести сторон, не выпадет цифра 7 – это считается достоверным событием, поскольку количество сторон предмета не соответствует данной в условии цифре. Или же, наоборот, в этом испытании выпадет цифра 7 – невозможное событие. Вероятность таких событий может равняться строго 0 или 1.
2) Полная группа событий – это тот случай, когда из нескольких событий, появление исключительно одно из них является достоверным, и все события в данном эксперименте являются несовместными попарно. Исходя из термина, следует теорема, которая гласит, что сумма вероятностей событий, образующих полную группу, численно равна единице. Далее формула по нахождению полной группы событий:
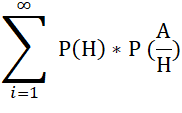 , (2)
, (2)
где:
H – гипотеза – несовместные попарно события, которые образуют полную группу.
Случайные события делятся на следующие виды:
1) Несколько событий в одном опыте называются равновозможными, если ни одно из них не является более возможным, чем другие, иначе говоря, все события имеют равные шансы и риски. Допустим, взять тот же самый игральный кубик. Выпадение всех цифр на нем является равновозможным событием, или, выпадение решки или орла, когда подбрасывают вверх монетку. Мы не можем предугадать, какое из представленных событий произойдет, но, тем не менее, известно, что каждое из них может случиться, поэтому принято считать, что у них есть равные шансы на появление.
2) Случай, наступление которого не зависит от появления иных, называется независимым событием, а явление, которое не может произойти без появления другого - зависимым. Например, из игральной колоды карт извлекли две карты. Необходимо найти вероятность, что вторая извлеченная карта окажется с мастью крести. Решение такой задачи, будет зависеть от того, какой масти извлекли первую карту (крести или нет). Если рассматривать независимые события, то можно привести другой пример: при подбрасывании двух монет, выпадет орел.
3) Совместные и несовместные события: если появление одного случая не исключает шансы на появление другого, то такие события носят термин совместные, с несовместными событиями все аналогично наоборот. [4]
В реальности происходят случайные явления, которые имеют не определенный характер связей. Поиск закономерностей в случайных явлениях - это задача теории вероятности. Она является инструментом для изучения скрытых и неоднозначных связей различных явлений во многих отраслях науки, техники, а также экономики. [5]
Таким образом, можно утверждать, что возникновение теории вероятностей не было случайностью в науке, а было вызвано необходимостью дальнейшего развития в устоявшей дисциплине – математика.
Список литературы
- Гмурман, В. Е. «Теория вероятностей и математическая статистика»: Учеб. пособие -- 12-е изд., перераб.- М.: Высшее образование, 2018.
- Ахтямов, А. М. «Теория вероятностей». -- М.: Физматлит, 2019.
- Вентцель Е. С. Теория вероятностей. -- 10-е изд., стер. -- М.: «Академия», 2020.
- Хамитов, Г. П., Ведерникова, Т. И. «Вероятности и статистики», БГУЭП. Иркутск: 2020.
- Чернова, Н. И. «Теория вероятностей», Новосибирск. 2021.



