Применение М-последовательностей в военных системах связи

Шумоподобные сигналы находят широкое применение в различных системах передачи информации, благодаря ряду достоинств, которыми они обладают: высокой помехозащищенностью; повышенной скрытностью; возможностью восстановления информации при воздействии узкополосных помех, все импульсы в периоде распределены равновероятно. Обладая этими преимуществами, ШПС сигналы очень часто используются в системах связи военного назначения, поскольку эффективное управление войсками возможно только с соблюдением режима секретности передачи команд, от которого зависит исход выполнения боевой задачи. В настоящее время широкое распространение получили фазоманипулированные сигналы, информационный параметр которых изменяется согласно заданному правилу, которое формируется М-последовательностью.

М-последовательность – бинарная (принимающая два значения) последовательность импульсов, характеризуемая рядом свойств, из которых основное это то, что автокорреляционная функция ее, измеренная на конечный интервал времени, представляет собой один узкий треугольник. М-последовательности, известные еще как последовательности Хаффмена, Голда, Касами, бент-последовательности, последовательности GMW, относятся к линейным рекуррентным последовательностям максимального периода [1, c.4].

М-последовательности обладают нижеперечисленными свойствами.

1. ПСП (псевдослучайная последовательность) является периодической с периодом из N импульсов.

2.  Величина боковых пиков периодической АКФ ПСП равна 1N .

3. М-последовательность в общем случае состоит из нескольких видов радиоимпульсов (отличающихся начальными фазами, несущими частотами и т.д.). Импульсы различного вида встречаются в периоде примерно одинаковое число раз, т.е. распределены на периоде равновероятно и удовлетворяют условию сбалансированности. Поэтому М-последовательности называют псевдослучайными.

4. Формируются М-последовательности на основе регистра сдвига с линейной обратной связью (РСЛОС). При этом, если регистр имеет k-разрядов (дискретных элементов задержки), и в М-последовательности используется алфавит из p различных видов импульсов (отличающихся, например, фазами), то N=pk-1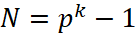 , откуда число разрядов регистра: k = log(N+1)/logp.

Следовательно, значительное увеличение числа импульсов N в периоде М-последовательности вызывает незначительное увеличение числа разрядов регистра, причем нулевая последовательность является запрещенной.

5. АКФ (автокорреляционная функция) усеченной М-последовательности, понимаемой как непериодическая последовательность с длиной N, имеет величину боковых пиков, близкую к 1N.

Формирование М-последовательности осуществляется системой из n-линейных регистров хранения сдвига и K сумматоров по модулю два, а также контура обратной связи. Длина М-последовательности определяется количеством сумматоров и максимально может составить M=2n-1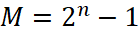 , где:

n – количество регистров хранения сдвига.

Максимально достижимое значение автокорреляционной функции:

RAτ=M, при τ=0-1, при τ≠0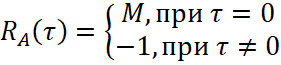

Рассмотрим в качестве примера по формированию М-последовательности систему, состоящую из n=4 регистров хранения сдвига и к=1 сумматоров по модулю два:

 

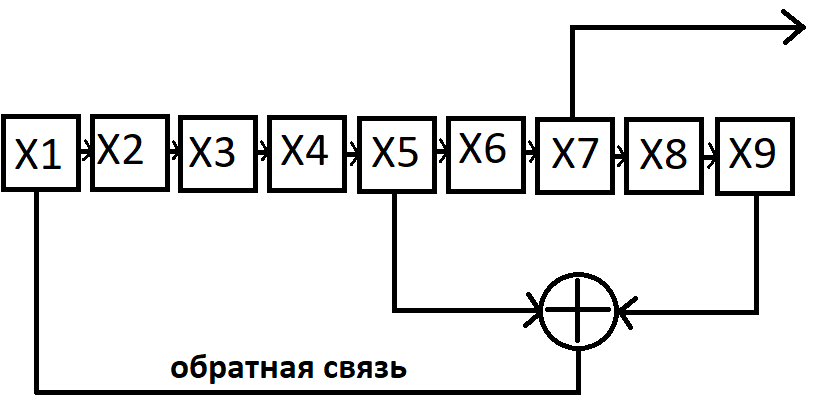
Работа по генерации М-последовательности осуществляется следующим образом.

С каждым новым тактом содержимое регистра сдвигается на одну позицию вправо.

Содержимое регистров Х5 и Х9 суммируются по модулю два. Результат суммирования по обратной связи подается на входной регистр Х1. Итоговая последовательность – это то, что формируется на выходе регистра Х7.

Представленная выше структура формирователя М-последовательности с модулятором была реализована в виде виртуального прибора в программной среде LabVIEW. Внешний вид виртуального прибора представлен на рисунке 1.

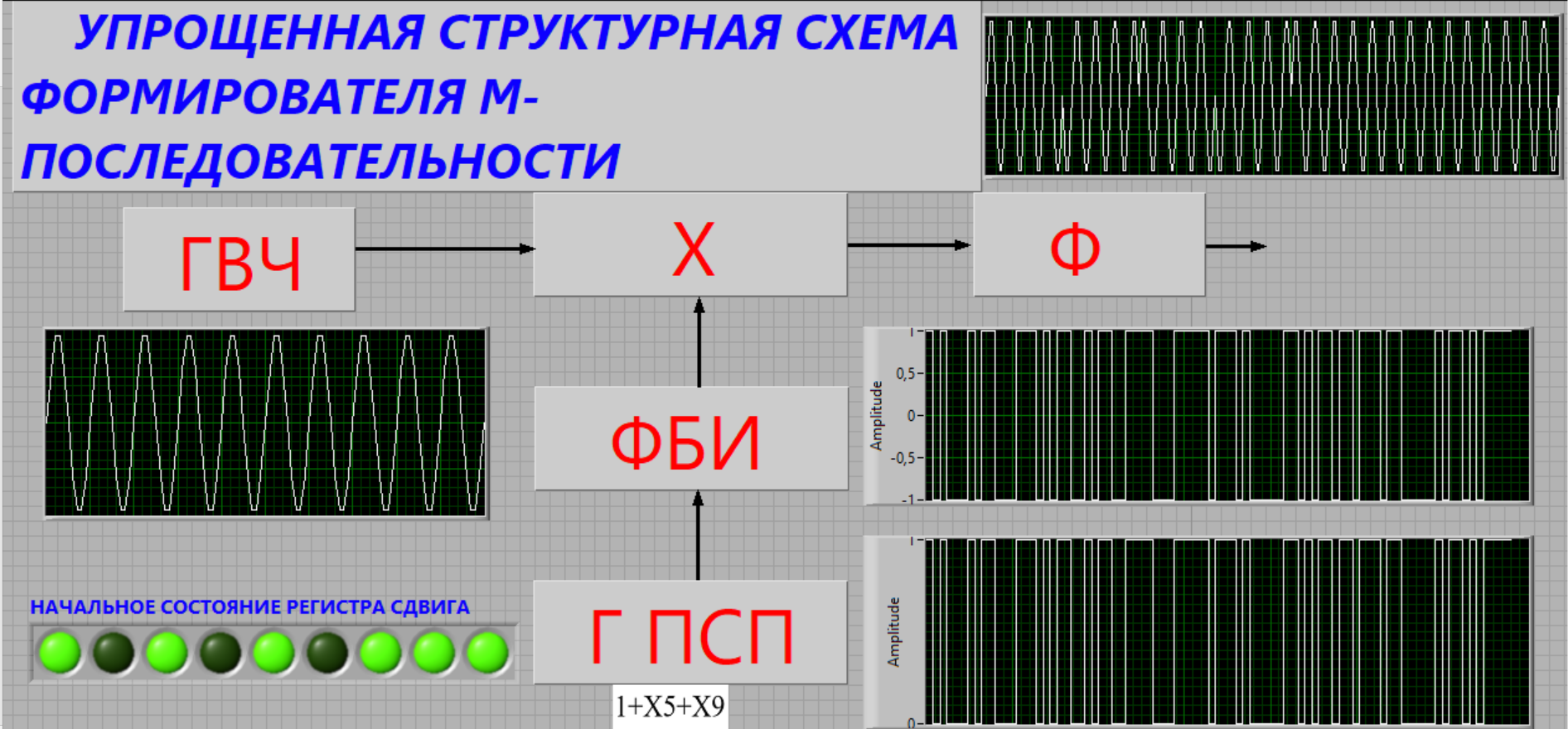Рисунок 1. Виртуальный прибор

 

На рисунке 2 представлены результаты моделирования: графики

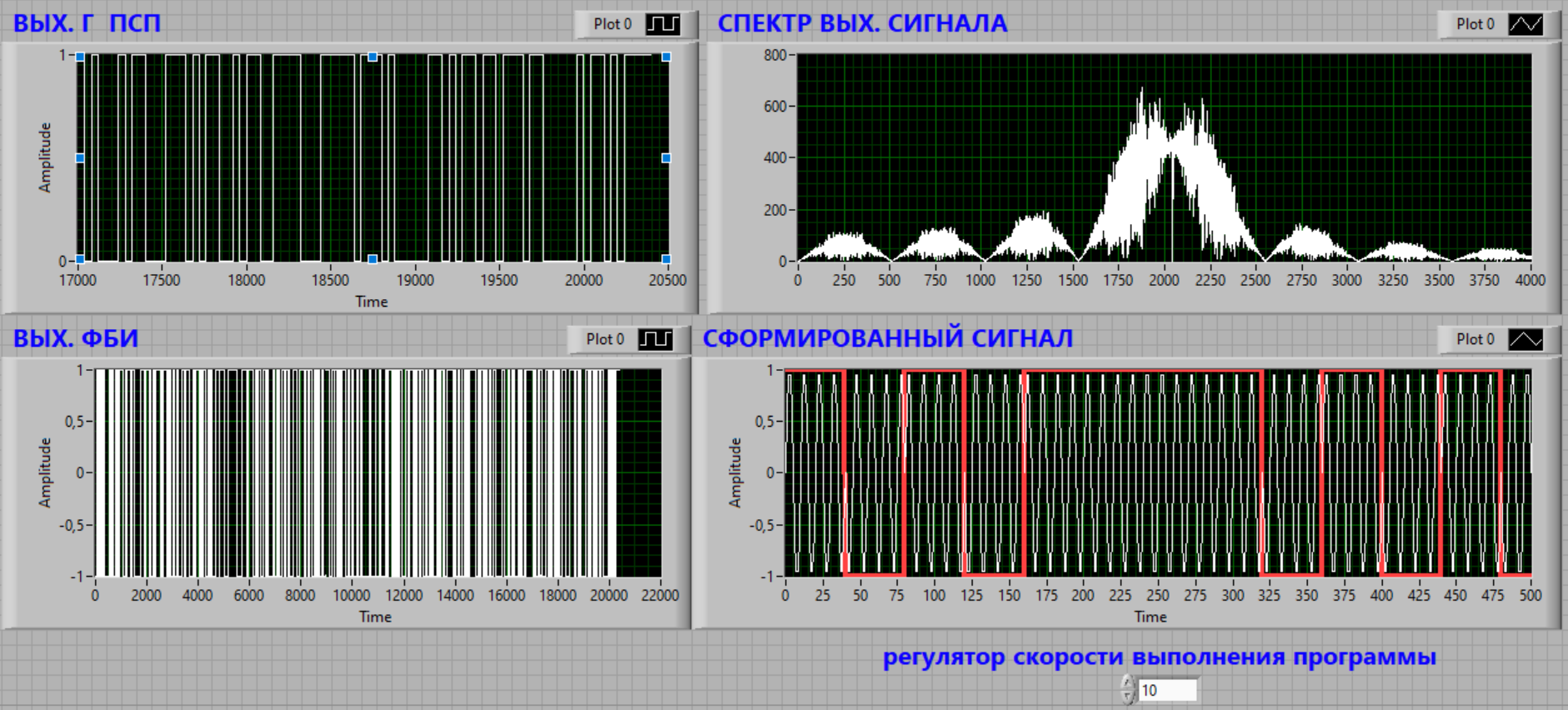
Рисунок 2. Графики формирователя М-последовательности

Структурная схема формирователя представлена на лицевой панели виртуального прибора. В ее состав входят:

1. Генератор высокой частоты, предназначенный для формирования несущего колебания, которое поступает на один из входов перемножителя, на второй вход которого подаётся сигнал с формирователя бинарных импульсов (Рисунок 3).

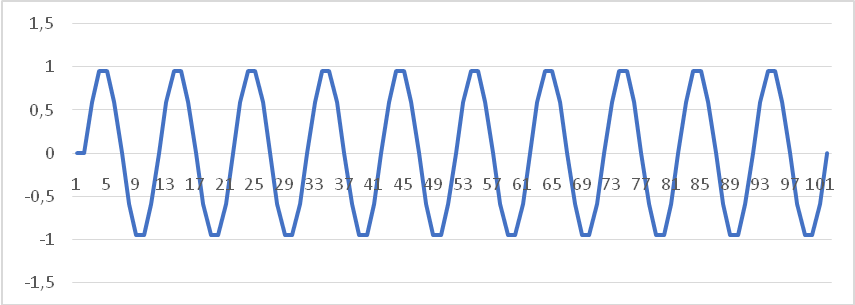
Рисунок 3. Несущее колебание

 

2. Формирование бинарных импульсов (ФБИ) происходит путем сдвига по оси Х сигнала, поступающего с генератора ПСП (Рисунок 4).

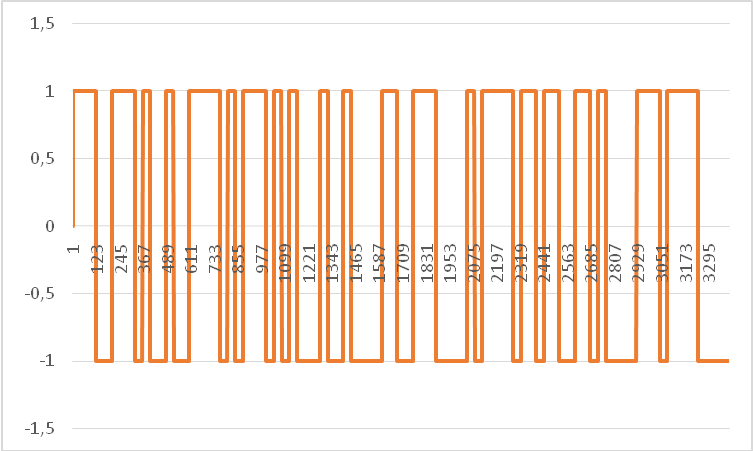
Рисунок 4. ФБИ сигнал

 

3. Выходной сигнал с перемножителя подаётся на полосовой фильтр для ограничения излучаемого спектра. Выходной сигнал фильтра представляет собой ВЧ ФМн сигнал (Рисунок 5).

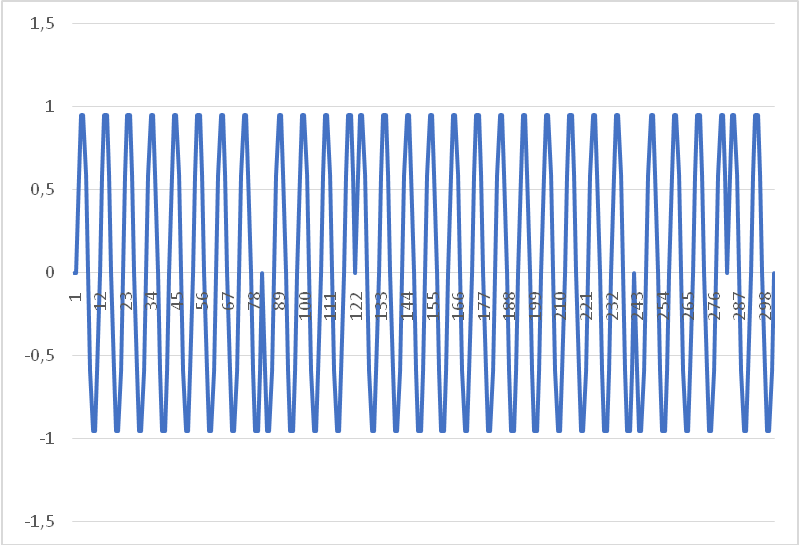
Рисунок 5. ВЧ ФМн

 

Таким образом, разработанный виртуальный прибор позволяет понять основные принципы формирования ШПС, проводить исследования характеристик различных М-последовательностей, использовать его в военных системах связи, обеспечивающих скрытую передачу информации, а также применять его для обучения курсантов принципам формирования ШПС.