РЕАЛИЗАЦИЯ ПАРАЛЛЕЛЬНОГО АЛГОРИТМА РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ХОЛЕЦКОГО

С момента появления компьютеров одной из их основных функций было выполнение трудоемких вычислений. При этом сложность поставленных задач растет быстрее, чем производительность отдельного процессора [1]. Многие современные вычислительные задачи не могут быть решены на однопроцессорных компьютерах, так как программа будет работать слишком долго или потребует большого количества ресурсов.

Актуальность данной темы заключается в том, что системы линейных алгебраических уравнений представляют собой математический аппарат, который широко используется при решении многих задач практического применения математики.

Разложение Холецкого (метод квадратного корня) - это представление симметричной положительно определенной матрицы A в виде

A = LL^Т                                                        (1)

 

где L - нижнетреугольная матрица со строго положительными элементами на диагонали.

Иногда разложение записывают в эквивалентной форме:

A = U^TU                                                       (2)

 

где U = LТ - верхнетреугольная матрица. Разложение Холецкого всегда существует и уникально для любой симметричной положительно определенной матрицы.

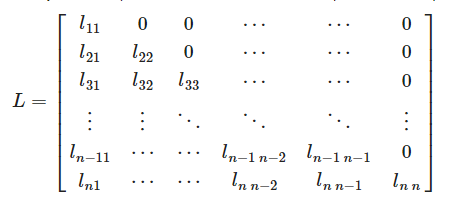
Рис. 1. Нижнетреугольная матрица L.

Это разложение можно использовать для решения системы линейных уравнений

Ax = b, если матрица A симметрична и положительно определена.

Такие матрицы часто возникают, например, при использовании метода наименьших квадратов и численном решении дифференциальных уравнений.

Выполнив разложение A = LLТ (1), решение x можно получить, последовательно решая две треугольные системы уравнений: Ly = b и LТx = y.

Это решение иногда называют методом квадратного корня. По сравнению с более общими методами, такими как разложение по Гауссу или LU, он численно более надежен и требует примерно половины арифметических операций.

Чтобы найти коэффициенты матрицы L, неизвестные коэффициенты матрицы L приравниваются к соответствующим элементам матрицы A.

Элементы матрицы L можно вычислить, начиная с левого верхнего угла матрицы, в соответствии с формулами на рисунке 2.

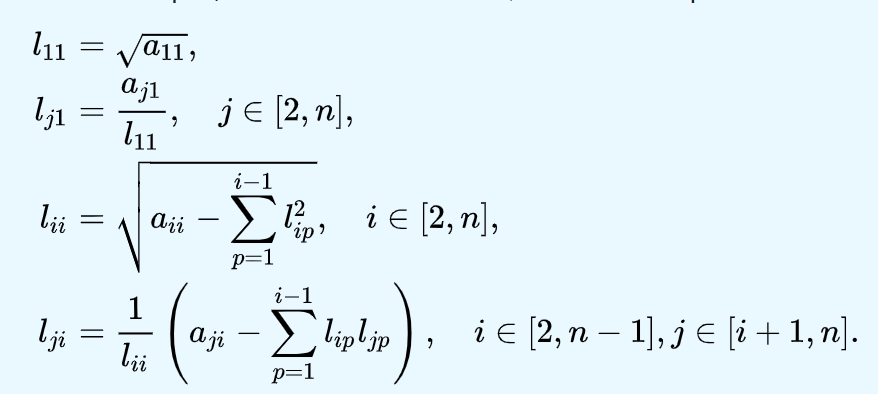
Рисунок 2. Формулы для вычисления элементов матрицы L.

 

Выражение под корнем всегда положительно, если A - вещественная положительно определенная матрица. Расчет происходит сверху вниз, слева направо, то есть сначала Lij, а затем Lii.

Симметрия матрицы позволяет хранить и вычислять лишь немногим более половины ее элементов, что почти вдвое экономит как объем памяти, необходимый для вычислений, так и количество операций по сравнению, например, с разложением по Гауссу [3]. В этом случае альтернативное (без вычисления квадратных корней) LU-разложение с использованием симметрии матрицы все же несколько быстрее, чем метод Холецкого (он не использует извлечение квадратного корня), но требует сохранения всей матрицы.

 

Разработка параллельного алгоритма для систем с общей памятью. Общая память - вычислительная память, в которой память рассматривается как разделяемый ресурс, и каждый из процессоров имеет полный доступ ко всему адресному пространству.

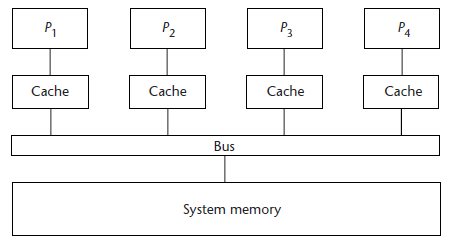
Рисунок 3. Система с общей памятью.

 

В простейшей реализации системы с общей памятью используют общую шину памяти для соединения всех процессоров. Эта конфигурация называется Uniform Memory Access (UMA) - равный доступ к памяти. Производительность многопроцессорных систем этого типа ограничивается пропускной способностью шины разделяемой памяти, и с увеличением количества процессоров, начиная с определенного их количества, производительность системы перестает расти [4]. Это связано с тем, что время ожидания доступа к шине разделяемой памяти резко увеличивается.

Для распараллеливания программ используется механизм создания потоков, для которых не создается отдельное адресное пространство, но которые на многопроцессорных системах также распределяются между процессорами. В языке программирования C можно напрямую использовать этот механизм для распараллеливания программ путем вызова соответствующих системных функций, а в компиляторах FORTRAN этот механизм используется либо для автоматического распараллеливания, либо в режиме установки директив распараллеливания в компилятор (этот подход также поддерживается компиляторами языка Си) [2].

Языки программирования и связанные с ними компиляторы для машин, таких как MSIMD, обычно предоставляют языковые конструкции, которые описывают «крупномасштабный» параллелизм. В рамках каждой задачи компилятор автоматически векторизует соответствующие циклы.

Для создания такой модели вычислений можно использовать стандартные инструменты операционной системы, такие как процесс, поток, или инструменты параллельного программирования высокого уровня, например, технологию OpenMP, которая будет использоваться для распараллеливания алгоритма в этой работе..

Разработка алгоритмов с использованием OpenMP. Объем вычислений будет зависеть от размерности исходной матрицы коэффициентов A и вектора свободных членов b. Чем больше их размер, тем больше будут матрицы L и LT, вектор y и вспомогательные массивы для вычислений.

Программа будет работать только с положительной симметричной матрицей A, поэтому для ее создания требуется алгоритм.

Количество потоков, а также размер матриц будут вручную записаны в коде. Циклы for, отвечающие за вычисление элементов матриц, результирующих и вспомогательных векторов, а также за транспонирование, будут подвергаться распараллеливанию [5].

Для измерения времени выполнения кода воспользуемся одной из функций OpenMP. Будет сохранено время до начала вычислений и время, полученное сразу после выполнения кода. Вычитая первое из второго значения, получаем время, за которое выполняются операции расчета. Для более точного расчета времени желательно повторить код в цикле несколько раз, а результат разделить на эту величину.

Алгоритм должен быть спроектирован так, чтобы при работе циклов элементы массива равномерно распределялись между потоками..

Программная реализация параллельного алгоритма решения СЛАУ методом Холецкого  Выбор технологии и средств реализации

Для решения поставленной в данной курсовой работе задачи были выбраны следующие технологии и инструменты:

1. Язык программирования C ++ для написания последовательных и параллельных алгоритмов.
2. Библиотека OpenMP для реализации алгоритма для систем с общей памятью

Сначала был реализован алгоритм генерации симметричной положительной матрицы.

 

 

Эта последовательность действий будет использоваться в последовательной и параллельной версиях программ.

 

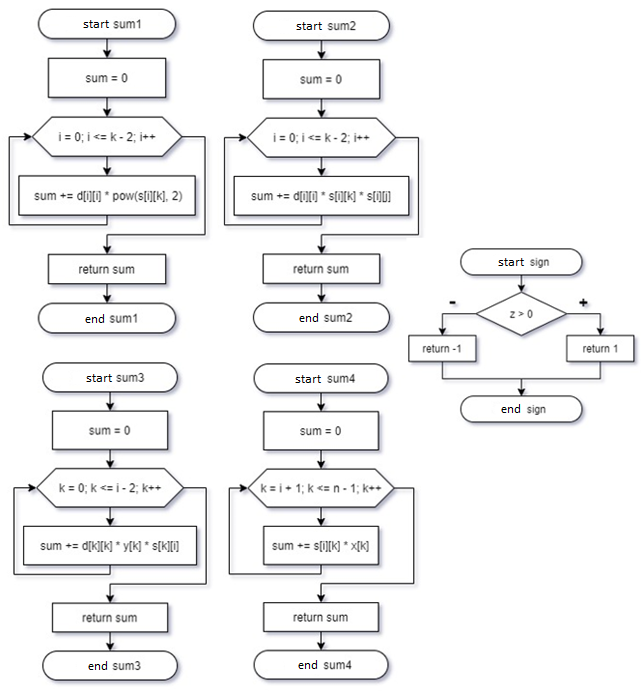
Рисунок 4. Блок-схемы функций.

 

Функции позволяют хранить фрагмент кода, который выполняет одну задачу, внутри определенного блока, а затем вызывать этот код всякий раз, когда он вам нужен. Затем была создана блок-схема алгоритма решения СЛАУ. (Рисунок 5)

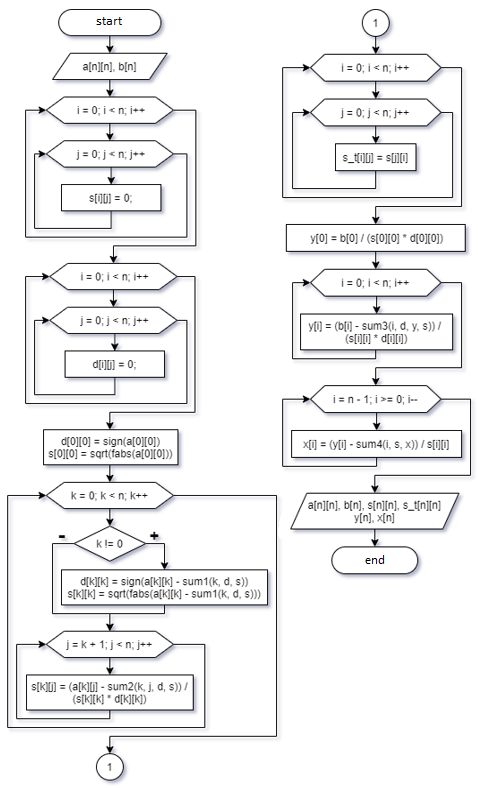
Рисунок 5. Блок-схема последовательного алгоритма..

A - матрица коэффициентов системы уравнений, s - верхний треугольник

матрица, элементы которой вычисляются по формулам, s_t - транспонированная матрица s, d - буферный вектор, y - вспомогательный вектор, x - результирующий вектор. Перечисленные выше структуры будут иметь размеры n и n * n, где n - переменная, значение которой будет расти с каждым экспериментом.