Математическое моделирование финансовых операций, опирающееся на множество методов и алгоритмов, используется очень широко в жизнедеятельности общества. Оно осуществляется с целью формирования определенных представлений о характере финансовых явлений и процессов [4, с. 223].
Это предопределяет необходимость овладения инструментами финансового анализа и прогнозирования изучаемых процессов. При этом компьютерные программы для финансовых исследований должны являться повседневным рабочим инструментом специалиста, связанного с обработкой финансовой информации [1, с. 105].
В настоящее время широко используется программное обеспечение, работающее в операционной системе Windows. Одной из составляющих этого обеспечения является программа Microsoft Excel, которая позволяет анализировать информацию, работать со встроенными финансовыми функциями и подбирать оптимальные решения различных финансовых задач [3, с. 77].
Рассмотрим задачу и проведем моделирование оптимального решения, используя финансовую функцию «БС» Microsoft Excel [2, с. 18].
Достаточно ли положить на счет 85.000 руб. для приобретения через 5 лет телевизора стоимостью 160.000 руб., если банк начисляет проценты ежеквартально при годовой ставке 12%.
Рассмотрим решение, используя финансовую функцию «БС» MS Excel [5, с. 130].
Для решения поставленной задачи составим таблицу исходных данных (рисунок 1).
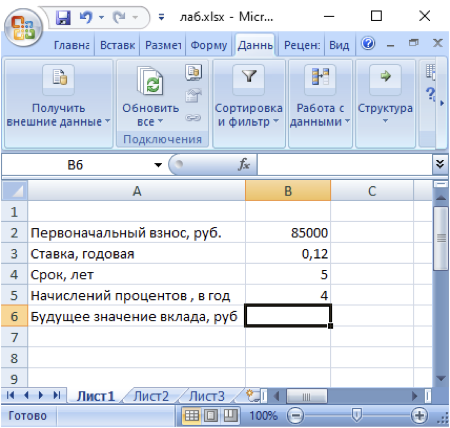
Рисунок - 1 Исходные данные
Введя, необходимые значения для функции «БС», в ячейку В6
=БС(12%/4;5*4;;-85000;1)
получим решение F = 153.519,45 руб. (рисунок 2).
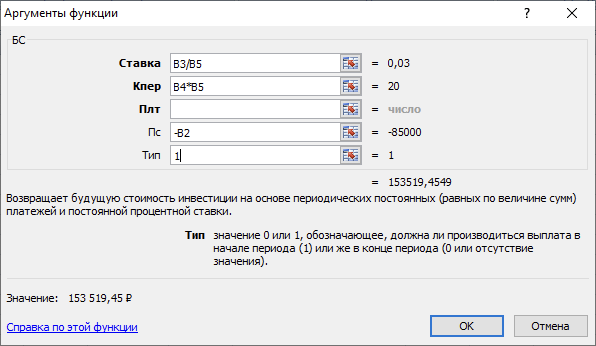
Рисунок – 2 Фрагмент окна MS Excel для функции «БС»
Проведем дополнительные варианты моделирования финансовой ситуации, а именно, рассмотрим два варианта:
- первоначально положить на счет большую сумму;
- воспользоваться банком, где предусмотрена большая процентная ставка.
1 вариант.
Для определения необходимой суммы, исходные данные задачи представим в виде таблицы и воспользуемся средством «Подбор параметра» из меню команды Сервис или Данные/Анализ «что-если»/Подбор параметра.
Иллюстрация решения представлена на рисунок 3.
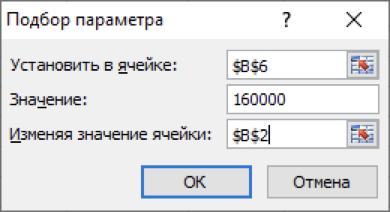
Рисунок - 3 Фрагмент окна MS Excel с заполненными
полями вкладки «Подбор параметра»
После подтверждения введенных данных в ячейке В6 установится значение 160.000,00р., а в ячейке B2 отобразится результат – 88.588,12 руб. (рисунок 4).
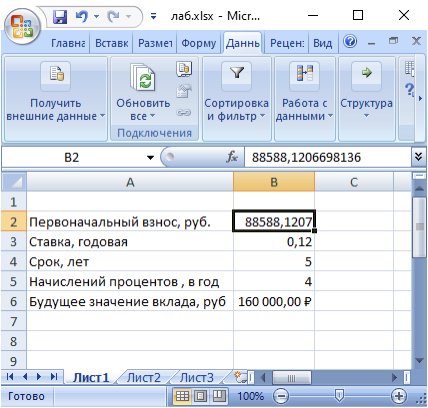
Рисунок - 4 Фрагмент окна MS Excel с заполненными
полями вкладки «Подбор параметра»
Это означает, что изначальная сумма, которая должна быть вложена, равна 88.588,12 рублей.
2 вариант.
В данном случае также можно применить средство Подбор параметра, изменяя ячейку, в которой находится процентная ставка (рисунок 5).
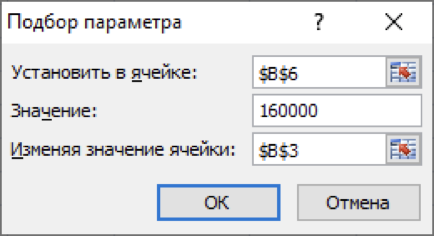
Рисунок - 5 Фрагмент окна MS Excel с заполненными полями вкладки
«Подбор параметра», изменяя ставку процента
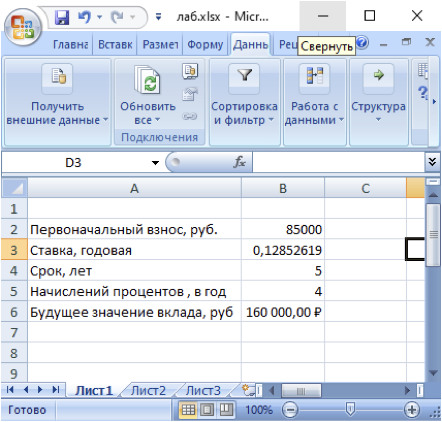
Рисунок - 6 Решение задачи, используя вкладку «Подбор параметра»,
изменяя ставку процента
Таким образом, годовая ставка при исходных данных должна составить примерно 12,9%.
Вывод: для достижения необходимой суммы потребитель может выбрать один из двух вариантов, а именно, либо увеличить первоначально вкладываемую сумму, либо определить вклад под большую процентную ставку.
Список литературы
- Колесникова С.В., Двойственный метод, как метод оптимизации экономических процесов, реализуемый в среде MS Excel. Новая наука: Проблемы и перспективы.. 2016. № 3-1. С.104-106.
- Колесникова С.В., Формирование отчетов, используя MS Excel при решении задач линейного программирования/ В сборнике: Информационные технологии в экономических и технических задачах. Сборник научных трудов Международной научно практической конференции. 2016. С.17-19.
- Колесникова С.В., Применение простых и сложных процентов к экономическим задачам. Новая наука: Проблемы и перспективы.. 2016. № 9-1. С.76-78.
- Колесникова С.В., Экономические задачи, сводимые к транспортным задачам. В сборнике: Человек, общество и государство в современном мире. Сборник научных трудов международной научно практической конференции: в 2 томах. 2016. С.220-223.
- Шишов В.Ф., Колесникова С.В., Киндаева Е.Н., Современные инструменты статистического анализа и прогнозирования при решении прикладных задач. Территория инноваций. 2019. №2(30). С. 130-136.



