Алгоритмы потоковой передачи с использованием дифференциальной конфиденциальности

Область потоковых алгоритмов была формализована Аланом и др. и породил большой объем работ, которые пересекаются со многими другими областями информатики, такими как теория, базы данных, сети и обработка естественного языка. Рассмотрим сценарий, в котором элементы данных генерируются один за другим, например, мониторинг IP-трафика или поиск. В общем, говоря, потоковые алгоритмы нацелены на обработку потоков данных, используя при этом лишь ограниченный объем памяти, значительно меньший, чем требуется для хранения всего потока данных.  Типичные проблемы потоковой передачи включают оценку моментов частоты, подсчет количества отдельных элементов в потоке, идентификацию тяжелых элементов в потоке, оценку медианы потока и многое другое.

Предположим, что элементы в потоке, а также запросы, выданные алгоритму, выбираются адаптивным (с сохранением состояния) злоумышленником. В частности, каждый элемент в потоке (и каждый из запросов) выбирается злоумышленником в зависимости от предыдущих элементов в потоке, предыдущих запросов и предыдущих ответов, данных нашим потоковым алгоритмом. В результате элементы в потоке больше не зависят от внутреннего состояния нашего алгоритма. Забывчивые алгоритмы потоковой передачи не могут обеспечить значимых гарантий полезности в такой ситуации. В этой работе мы стремимся разработать устойчивые к противоборству потоковые алгоритмы, которые поддерживают (доказуемую) точность в отношении таких адаптивных противников, при этом, конечно, сводя требования к памяти и времени выполнения к минимуму. Мы подчеркиваем, что такие зависимости между элементами в потоке и внутренним состоянием алгоритма могут возникать непреднамеренно (даже когда нет “противника”). Например, рассмотрим большую систему, в которой алгоритм потоковой передачи используется для анализа данных, поступающих из одной части системы, отвечая на запросы, генерируемые другой частью системы, но эти (предположительно), разные части системы соединены через контур обратной связи. В таком случае больше не верно, что элементы в потоке генерируются независимо от предыдущих ответов, и большинство существующих алгоритмов потоковой передачи не смогут обеспечить значимых гарантий полезности.

Напомним, что (как правило) в режиме забывчивости, требования к памяти растут только логарифмически с увеличением количества запросов, которые мы хотим поддерживать. Для адаптивной настройки можно легко покажите, что достаточно увеличения объема памяти O (m). Этого можно достичь, например, запустив m независимых копий алгоритма (где мы передаем входной поток каждой из копий) и используя каждую копию для ответа не более чем на один запрос. Можем ли мы сделать лучше?

Этот вопрос побудил к недавнему направлению работы, которое сосредоточено на построении надежных алгоритмов потоковой передачи в режиме состязательности. Формальная модель, которую мы рассматриваем, была недавно выдвинута Бен - Элиэзером и др., которые представили состязательно надежные потоковые алгоритмы для многих проблем в модели только для вставки, т.е. когда поток содержит только положительные обновления. Более того, их результаты распространяются на все потоки (где разрешены как положительные, так и отрицательные обновления), при условии, что количество отрицательных обновлений невелико. Вопрос оставался в значительной степени открытым для общей модели турникета, где могло быть большое количество негативных обновлений.

1 Существующие результаты

Теперь мы дадим неофициальный обзор методов Бен - Элиэзера и др. Этот интуитивный обзор, как правило, чрезмерно упрощен и скрывает многие трудности, возникающие при фактическом анализе.

Рассмотрим поток обновлений u1,...,um, где каждое обновление ui ∈ X поступает из домена X размером |X | = n. Для i ∈ [m] мы пишем ui = (u1,...,ui), чтобы обозначить первые i элементов потока. Пусть д : X∗ → R - функция, например, д может подсчитывать количество различных элементов в потоке. Состязательно надежные алгоритмы потоковой передачи с использованием дифференциальной конфиденциальности.

На каждом временном шаге i, после получения следующего элемента в потоковом пользовательском интерфейсе, наша цель – вывести приближение для д(ui). Чтобы проиллюстрировать результаты Бен - Элиэзера и др., давайте рассмотрим проблему отдельных элементов (в модели только вставки, где в потоке нет удалений). В частности, после каждого обновления пользовательского интерфейса нам нужно выводить оценку отдельных элементов в потоке, т.е. д(ui) = |{uj: j ∈ [i]}|. Обратите внимание, что это количество монотонно увеличивается. Кроме того, поскольку мы стремимся к мультипликативной ошибке (1 ± α), даже при том, что поток большой (длиной m), количество раз, когда нам действительно нужно изменять оценки, которые мы публикуем, довольно таки мало, примерно 1 α log m раз. (Заметим, что это неверно, если поток может содержать удаления, также известные как модель турникета.) Неофициально идея Бен - Элиэзера и др. состоит в том, чтобы параллельно выполнить несколько независимых эскизов и использовать каждый эскиз для публикации ответов по части потока, в течение которой оценка остается постоянной. Более подробно, общее преобразование Бен - Элиэзера и др. (применимое не только к проблеме отдельных элементов) основано на следующем определении.

Определение 1.1 (номер переворота). Учитывая функцию д, (α,m)-число переворота д, обозначаемое как λα,m (д), является максимальным числом раз, когда значение д может изменяться (увеличиваться или уменьшаться) в коэффициент (1 + α) в течение потока длиной m.

Общая конструкция Бен - Элиэзера и др. для функции д выглядит следующим образом:

(1) Создайте экземпляр λ ≥ λα,m (д) независимых копий алгоритма потоковой передачи с забвением для функции д и установите j = 1.

(2) Когда появится следующее обновление пользовательского интерфейса:

(a) Передайте пользовательский интерфейс всем копиям λ.

(b) Опубликуйте оценку, используя j-ю копию (округленную до ближайшей степени (1 + α)). Если эта оценка отличается от предыдущей оценки, то установите j ← j + 1.

Бен-Элиэзер и др. показали, что это может быть использовано для преобразования, не обращающего внимания потокового алгоритма для д в состязательно надежный потоковый алгоритм для . Кроме того, накладные расходы с точки зрения объем памяти составляет всего λα,m (д), что обычно мало в модели только для вставки (обычно λα,m (д) 1 α log m). Более того, Бен-Элиэзер и др. показали, что их методы распространяются на модель турникета (когда поток может содержать удаления), при условии, что количество отрицательных обновлений невелико (и поэтому λα,m (д) остается небольшим).

Теорема 1.2. Исправьте любую функцию д, и пусть A будет забывчивым потоковым алгоритмом для д, который для любого α, δ > 0 использует пространство L(α, δ) и гарантирует точность α с вероятностью успеха 1−δ для потоков длиной m. Тогда существует состязательно надежный алгоритм потоковой передачи для д, который гарантирует точность α с вероятностью успеха 1 − δ для потоков длиной m, использующих пространство:

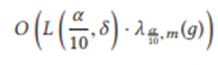
2. Наши результаты

Мы устанавливаем связь между состязательной надежностью алгоритмов потоковой передачи и дифференциальной конфиденциальностью - моделью, которая доказуемо гарантирует защиту конфиденциальности при анализе данных. Рассмотрим базу данных, содержащую (конфиденциальную) информацию, относящуюся к отдельным лицам. Алгоритм, работающий на такой базе данных, считается дифференциально частной, если ее результаты не раскрывают информацию, относящуюся к какому-либо отдельному лицу в базе данных. Более формально, дифференцированная конфиденциальность требует, чтобы данные ни одного человека не оказывали существенного влияния на распределение выходных данных. Интуитивно это гарантирует, что все, что узнается о человеке, также может быть изучено с произвольно измененными его данными (или без его данных). Формально у нас есть следующее определение.

Определение 1.3.  Пусть A - рандомизированный алгоритм, работающий с базами данных. Алгоритм A является (έ, δ) - дифференциально частным, если для любых двух баз данных S, S, которые отличаются по одной строке, и любого подмножества результатов T , мы имеем

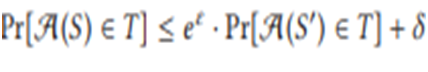
Наш главный концептуальный вклад состоит в том, чтобы показать, что понятие дифференциальной конфиденциальности может быть использовано в качестве инструмента для создания новых надежных в отношении состязательности алгоритмов потоковой передачи. В двух словах, идея состоит в том, чтобы защитить внутреннее состояние алгоритма, используя дифференциальную конфиденциальность. Грубо говоря, это ограничивает (точным образом) зависимость между внутренним состоянием алгоритма и выбором элементов в потоке и позволяет нам анализировать гарантии полезности алгоритма даже в адаптивной настройке. Обратите внимание, что дифференциальная конфиденциальность здесь не используется для защиты конфиденциальности элементов данных в потоке. Скорее всего, здесь используется дифференциальная конфиденциальность для защиты внутренней случайности алгоритма.

Для многих задач, представляющих интерес, даже в общей модели турникета (с удалениями), этот метод позволяет нам получать состязательно надежные потоковые алгоритмы с сублинейным пространством.  Насколько нам известно, наша методика является первой, которая обеспечивает значимые результаты для общей модели турникета. Кроме того, для интересных режимов параметров наш алгоритм превосходит результаты  Бен - Элиэзера и др. также для модели только для вставки (строго говоря, наши результаты для модели только для вставки несравнимы с их работой).

Мы получаем следующую теорему.

Теорема 1.4. Зафиксируйте любую функцию д и зафиксируйте α, δ > 0. Пусть A - алгоритм потоковой передачи без учета д, который использует пространство L и гарантирует точность α 10 с вероятностью успеха 9 10 для потоков длиной m. Тогда существует состязательно надежный алгоритм потоковой передачи для д, который гарантирует точность α с вероятностью успеха 1 − δ для потоков длиной m, использующих пространство

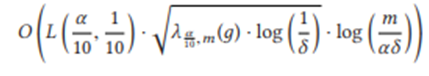
По сравнению с Беном - Элиэзером и др., наша пространственная граница растет только как √ λ, а не линейно по λ. Это означает, что в общей модели турникета, когда λ может быть большим, мы получаем значительное улучшение за счет дополнительных логарифмических коэффициентов. Кроме того, поскольку λ обычно масштабируется, по крайней мере, линейно с 1 / α, мы получаем улучшенные оценки даже для модели только для вставки с точки зрения зависимости объема памяти в 1 / α (опять же, за счет дополнительных логарифмических коэффициентов).

3. Другие связанные результаты

За последние несколько лет дифференциальная конфиденциальность зарекомендовала себя как важное алгоритмическое понятие (даже когда конфиденциальность данных не вызывает беспокойства) и оказалась полезной во многих других областях, таких как машинное обучение, проектирование механизмов, безопасные вычисления, теория вероятностей, безопасное хранение и многое другое. В частности, наши результаты используют связь между дифференциальной конфиденциальностью и обобщением, которая была впервые обнаружена Дворком и др. в контексте адаптивного анализа данных.