Расчетная модель оптимальных параметров игольчатого оребрения конденсаторов систем тсг

Одной из ключевых задач при проектировании систем термостабилизации грунта (далее – ТСГ), является обоснование выбора типа оребрения конденсаторов. Конденсаторы, как и другие теплообменные аппараты, как правило, работают с тепловыми потоками высокой плотности, а потому определение оптимальных параметров (форма, размер, число ребер) ребристой поверхности теплообмена представляет собой сложную нелинейную задачу. Особенность исследуемого конденсатора заключается в шахматном расположении элементов ребристой поверхности для увеличения скорости теплообмена в условиях естественной конвекции.

          Теплообмен при свободной конвекции в неограниченном пространстве

          Из исследований свободной конвекции над вертикальными конденсаторами, известно, что кривизна оребрения увеличивает скорость теплопередачи по сравнению с плоскими поверхностями в ламинарных режимах. Зарубежные исследователи также получили выражения коэффициента кривизны в зависимости от диаметра конденсатора, длины, чисел Прандтля и Грасгофа. При этом важно уметь переводить скорости теплопередачи от криволинейных поверхностей к эквивалентам плоских элементов оребрения. Существуют различные способы решения поставленной задачи в рамках вычислительной гидродинамики. В качестве криволинейной поверхности, авторы статьи в данной работе, будут рассматривать игольчатые шипы, расположенные в шахматном порядке имеющие вогнутый параболический профиль. Потому как традиционный метод, основанный на использовании объема жидкости для расчета потока конденсации путем отслеживания границы раздела между конденсатом и газовой смесью (воздухом) не предполагает каких-либо эмпирических данных и достаточно требователен с точки зрения пространственного разрешения. [1].

          Постановка задачи

          Необходимо определить тепловой поток, отводимый круглым шипом прямоугольного профиля диаметром δ  = 10 мм, высотой h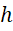  = 100 мм. Шипы расположены в шахматном порядке с шагом s1=s2= 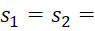 30 мм. Скорость потока охлаждающего воздуха ωв= 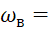 5 м/с, температура t= 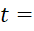 40 ˚C. Температура шипа в основании tо= 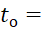60 ˚C. Материал шипа – сталь марки 09Г2С (λ= 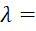 80 Вт/(м∙ 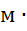 ˚C)). Задача – провести сравнительный анализ для кольцевого и игольчатого оребрения при одинаковых условиях.

          Для определения коэффициента теплоотдачи игольчатого шипа рассмотрим зависимость для вынужденного поперечного обтекания стержня. При этом физические свойства воздуха при нормальном атмосферном давлении и расчетной температуре составят: νв=1,66∙10-5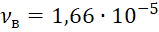  м²/с, λв=0,0271 Вт/(м∙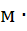  ˚C), Prв=0,711 .

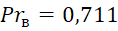          Найдем число Рейнольдса:

 

Re=ωв∙δ0νв=5∙0,011,66∙10-5=3012 .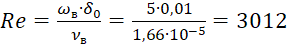

 

          Определим число Нуссельта для шахматного пучка:

 

Nu=0,41∙Re0,6∙Prв0,33∙s1s216=0,41∙30120,6∙0,7110,33∙303016=7,5 .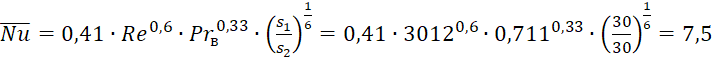

 

          Определим коэффициент теплоотдачи:

 

α=Nu∙λвδ0=7,5∙0,02710,01=20,2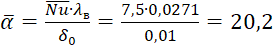  Вт/(м2∙ 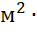 ˚C).

 

          Для шипов одинаковой высоты и одинаковой площади основания, характеристический параметр шипа прямоугольного профиля определяется как:

 

N=4αλδ0∙h=4∙20,280∙0,01∙0,1=1,006 .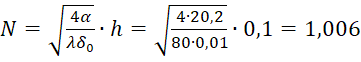

 

          Согласно [2] оптимальный размер шипа прямоугольного профиля составляет Nопт=0,919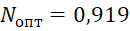 . Полученный результат близок к этому значению.

          Эффективность одного шипа определим по формуле:

 

η=thNN=0,761,00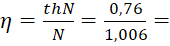6= 0,76.

         

При этом тепловой поток, отводимый одним шипом, составляет:

 

Q0=α∙Δt∙F∙η=20,2∙20∙(3,14∙0,1∙0,01)∙0,76= 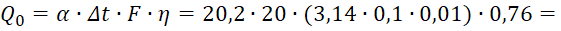0,97 Вт.

Определим оптимальные размеры шипа прямоугольного профиля по следующим зависимостям:

 

δ0.опт=0,915∙Q02α∙λ∙Δt213=0,915∙0,97220,2∙80∙20213=0,0103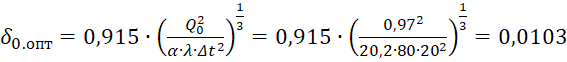  м = 10,3 мм.

 

Vопт=0,29∙Q05α4∙λ∙Δt513=0,29∙0,97520,24∙80∙20513= 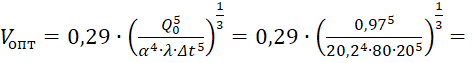0,0000078 м³.

 

hопт=4V2p+1πδ0.опт2=4∙0,0000078∙(2∙0+1)3,14∙0,01032=0,0932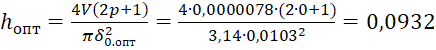  м = 93,2 мм.

 

 

Определим оптимальные размеры кольцевого ребра прямоугольного профиля при тех же условиях, что и для игольчатого оребрения.  Величину теплового потока, отводимого одним ребром, примем равным Q0= 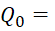10 Вт. Внутренний радиус ребра примем равным диаметру испарителя и эквивалентном диаметру r1=d1=dэ=33,7 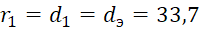 мм. Высота ребра h=50 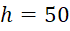 мм. Толщина ребра δ1=10 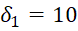 мм.

Вычислим площадь поперечного сечения ребра:

 

S=2πrδ1=2∙3,14∙33,7∙10=2116,4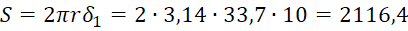  мм².

 

Согласно [2, П1-5а] число Нуссельта определяется по формуле:

 

Nu=0,025Sdэ0,4∙hdэ-0,2Re0,87Pr0,4=0,025∙2116,433,70,4∙5033,7-0,2∙30120,87∙0,7110,4=112,26 .

 

Отсюда, коэффициент теплоотдачи будет равен:

 

α=Nu∙λвδ1=112,26∙0,02710,01=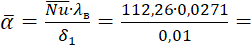 304,2 Вт/(м2∙ 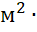 ˚C).

 

Найдем безразмерные параметры:

 

Q=Q02πr1∆t=102∙3,14∙0,0337∙20=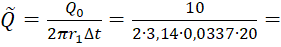 0,001.

 

Z=2αr1λ12=2∙304,2∙0,03378012=0,506.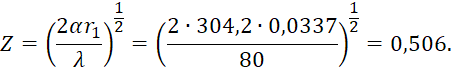

 

Определим ω,v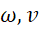  из номограммы [2, Рис.1-12].

 

ω=6,4; v=1 .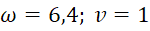

Найдем оптимальные размеры кольцевого ребра прямоугольного профиля из следующих зависимостей:

 

δ=r1ω=3,376,4=0,527  см = 5,27 мм.

 

V=πr13v=3,14∙3,373∙1=120,176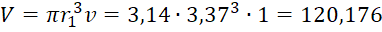  см³ = 120176 мм³.

 

r2=r12+Vπδ12=33,72+1201763,14∙5,2712=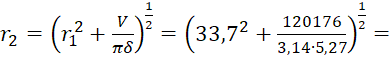  91,7 мм.

 

Определим эффективность ребра:

 

η=2QZ2ωv=2∙0,0010,5062∙6,4∙1= 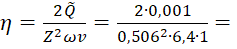0,001.

 

Выводы

В результате расчетов было установлено, что оптимальная толщина игольчатого шипа прямоугольного профиля составляет 10,3 мм, а кольцевого ребра прямоугольного профиля, при тех же условиях, – 5,27 мм. При этом один шип способен отвести 0,97 Вт тепла, а все ребро отводит – 10 Вт тепла. Тем не менее при таких условиях, кольцевое ребро по сравнению с игольчатым шипом абсолютно неэффективно.