Рассмотрим некоторые распространенные методы доказательства неравенств на конкретных примерах.
Задача 1. Доказать неравенства:
![]()
Доказательство.
а) Заметим, что числа ![]()
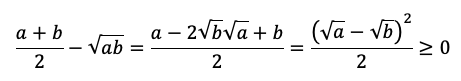
Таким образом, неравенство доказано. Заметим, что мы также доказали, что неравенство Коши обращается в равенство лишь при ![]()
б) Воспользуемся неравенством Коши для чисел ![]()
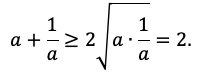
Замечание: неравенство о средних справедливо и для n неотрицательных чисел, где n - любое натуральное. А именно:
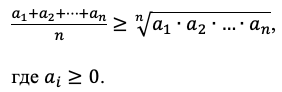
При этом, аналогично случаю для двух чисел, выражение слева - среднее арифметическое чисел, а справа - среднее геометрическое.
Докажем аналогичное неравенство для n=4. В общем случае доказательство проходит методом математической индукции.
Будем пользоваться неравенством о средних для n = 2:
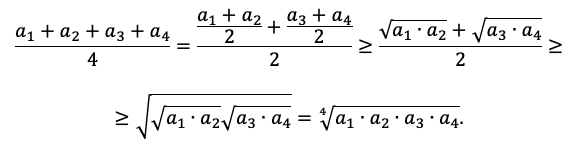
Задача 2. Докажите, что
Доказательство: имеем
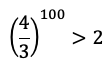
Но
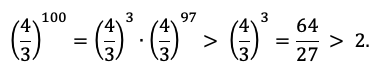
Задача 3. Докажите неравенство:
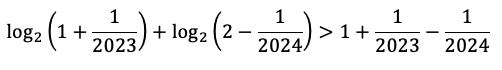
Доказательство: докажем, что для всех
Для этого достаточно показать, что
Так как![]() то, применяем доказанное неравенство, получим
то, применяем доказанное неравенство, получим
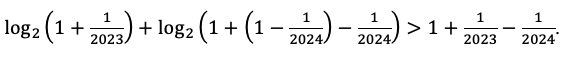
Бывают задачи несколько другого плана.
Задача 4. Без использования вычислительных средств выяснить, какое число больше: ![]()
Решение. Сравним эти два числа, вычислим их разность
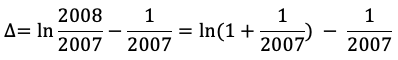
Введем в рассмотрение функцию с областью определения ![]()
![]()
Тогда величина ![]()
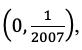 так как
так как
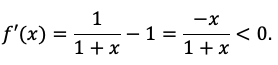
Имеем ![]() отсюда вытекает, что величина
отсюда вытекает, что величина ![]() или
или
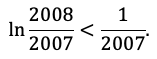
Помимо требуемого числового неравенства, здесь доказано более общее утверждение, если выбрать область определения функции
при
![]()
при
Задача 5. Что больше 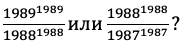
Решение. Введем в рассмотрение функцию ![]()
Тогда исходная задача сводится к сравнению двух значений функции
Проверим монотонность функции
![]()
для чего найдем ее производную
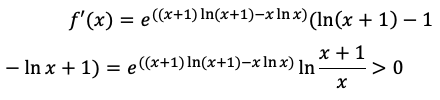
при
![]()
и
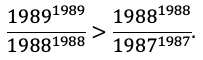
Задача 6. Доказать неравенство
![]()
Доказательство. Прологарифмируем обе части этого неравенства:
![]()
Используя неравенство
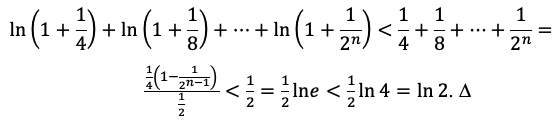
Список литературы
- Бронштейн Е. М., Водопьнов В. В., Муртазина Р. Д., Чебанов В. И. Задачи студенческих олимпиад по математике. – Уфа: УГАТУ, 2011. – 72 с.
- Иванова Н. И. Предметные олимпиады в вузе: теория и практика. Сборник докладов заочного научно-методического семинара «Актуальные проблемы преподавания математики в высшем учебном заведении». Кострома: Военная академия им. Тимошенко, 2013. – 372 с.
- Олехник С. Н., Потапов М. К., Пасиченко П. И. Уравнения и неравенства. Нестандартные методы решения. – М.: Факториал, 1997. – 219 с.
- Ройтенберг В. Ш., Оленикова Ю. К., Сидорова Л. А. Задачи студенческих математических олимпиад ЯГТУ. Учебное пособие. – Ярославль: ЯГТУ, 2012. – 127 с.



