ПАРАМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЛОПАТОК ЦЕНТРОБЕЖНОГО НАСОСА НА ОСНОВЕ КРИВЫХ БЕЗЬЕ

В процессе проектирования современных лопаточных машин возникает острая необходимость в эффективных методах создания высокоточных геометрических моделей. Ключевая задача заключается в том, чтобы обеспечить не только высокую точность моделирования, но и возможность оперативной модификации конструкции в соответствии с изменениями технических требований.

Наиболее проблематичным аспектом является разработка трёхмерных моделей проточной части. При использовании классических CAD-технологий инженеры сталкиваются с серьёзными ограничениями: даже опытному специалисту требуется несколько рабочих дней для создания одной модели. Подобная длительность процесса существенно затрудняет проведение всестороннего параметрического анализа и оптимизацию геометрических параметров.

На сегодняшний день в инженерной сфере сформировались две основные стратегии автоматизации проектирования:

• Полуавтоматизированные системы, в которых программное обеспечение выполняет расчёт промежуточных сечений, а финальная доработка модели осуществляется специалистом вручную
• Универсальные CAD-комплексы, обладающие определённым набором функций, но ограниченной гибкостью применения

Анализ доступных решений демонстрирует, что существующие программные продукты не способны обеспечить необходимый уровень гибкости при моделировании проточной части [4]. Это обстоятельство делает актуальной разработку специализированных параметрических моделей, способных эффективно решать задачи проектирования.

Схема меридианного сечения колеса центробежного насоса, включающая параметрические обозначения, показана на рисунке 1.1.

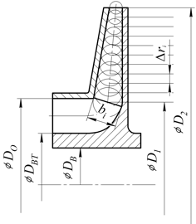
Рисунок 1. Меридианное сечение рабочего колеса

Параметры:

D₁ – Диаметр окружности, проходящей через средние точки входных кромок лопастей;

D₂ – Наружный диаметр рабочего колеса;

D_В – Диаметр вала рабочего колеса

D_ВТ – Диаметр втулки (ступицы) колеса;

D_O – Диаметр входа в колесо;

b_i –  Ширина межлопастного канала на соответствующем радиусе.

Параметрическое моделирование лопаток представляет собой ключевой аспект в проектировании, где особую роль играют кривые Безье. Этот метод построения кривых демонстрирует ряд существенных преимуществ в процессе моделирования.

Главные достоинства применения кривых Безье:

• точность моделирования достигается при использовании минимального количества опорных точек, что существенно упрощает процесс проектирования;
• плавность переходов обеспечивается за счёт C²-непрерывности, гарантирующей отсутствие изломов и резких изменений кривизны;
• гибкость управления формой позволяет вносить локальные изменения без влияния на общую геометрию.

Практическое применение кривых Безье в моделировании лопаток позволяет существенно сократить количество параметров, необходимых для описания геометрии. Это значительно облегчает последующую оптимизацию конструкции.

Математическая основа метода представлена кубической кривой Безье — параметрической кривой третьего порядка. Она формируется четырьмя базовыми точками: P₀​, P₁​, P₂​, P₃​, которые определяют форму кривой.

Математическое описание кубической кривой Безье выражается соответствующим уравнением.

         B(t)=(1-t)³ P₀+3t(1-t)²P₁+3t²(1-t) P₂+t³P₃                                                               (1)

Топология профиля, показанная на рисунке 1, предлагается для использования в данной методике.

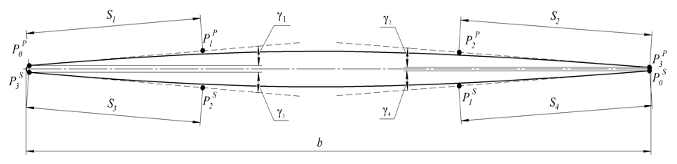
Рисунок 2. Профиль лопатки

Положение контрольных точек определяется на основе заданных углов γ₁–γ₄, а также расстояний от начальных и конечных точек, положение которых остаётся фиксированным. Входная и выходная кромки профиля описываются дугами окружностей, обеспечивая плавное сопряжение с основным контуром.

В рассматриваемом подходе параметры моделирования классифицируются следующим образом:

1. Управляемые — параметры, варьируемые в ходе оптимизационного процесса и напрямую влияющие на формирование обводов профиля.
2. Фиксированные — значения, неизменные в рамках рассматриваемой геометрической схемы.
3. Зависимые — величины, рассчитываемые на основе функциональных связей с управляемыми параметрами.

Согласно заложенной топологии, контур профиля задаётся двумя кривыми Безье: одна описывает напорную сторону с последовательными контрольными точками P₀^P–P₃^P, другая — всасывающую сторону с точками P₀^S–P₃^S. Начальные и конечные точки обеих кривых жёстко привязаны к окружностям, определяющим геометрию кромок.

Представленный подход позволяет существенно упростить процесс построения геометрии профиля при сохранении высокой точности и гибкости в управлении формой. Ключевым преимуществом методики является возможность оперативной модификации конструкции в рамках ограниченного набора параметров, что особенно важно при выполнении задач многовариантной оптимизации.

Внедрение данной методики в инженерную практику может существенно сократить сроки проектирования, повысить качество моделей и расширить возможности для автоматизации оптимизационных процедур. Полученные результаты создают основу для дальнейших исследований в области интеграции параметрических моделей в современные CAD/CAE-системы и применения методов численного моделирования при проектировании лопастных машин.