ПРИМЕНЕНИЕ НЕЧЁТКИХ НЕЙРОННЫХ СЕТЕЙ В ЗАДАЧЕ ПРОФЕССИОНАЛЬНОГО ОТБОРА

ВВЕДЕНИЕ

Современный рынок труда характеризуется высоким уровнем конкуренции и большим объёмом кандидатов на различные позиции. В организациях накапливается огромное количество данных об успешности сотрудников и соискателей, включая результаты тестов, оценки компетенций, психологические профили и др. В таких условиях ручные или традиционные алгоритмические методы отбора становятся всё менее эффективными: они не успевают адаптироваться к изменчивым требованиям, демонстрируют ограниченную точность и часто не учитывают взаимозависимости между множеством факторов [5].

В данной статье будет рассмотрен способ применения нечётких нейронных сетей в сфере профессионального отбора.

Нечёткие нейронные сети

Нечёткие нейронные сети – это гибридные системы, сочетающие принципы нечёткой логики и искусственных нейронных сетей. Они предназначены для обработки нечётких, шумных или неполных данных при решении сложных задач классификации, прогнозирования и управления.

Нечёткая логика позволяет формализовать экспертные знания через приведение входных числовых значений к лингвистическим переменным с помощью функции принадлежности, а нейросети обеспечивают адаптивное обучение и построение правил нечёткого вывода. Нечёткие правила формируются в процессе обучения сетей.

Нечёткие нейронные сети успешно применяются в интеллектуальных системах управления (робототехнике, автоматике, системах жёсткого управления), обработке изображений, анализе временных рядов, распознавании образов и обработке естественного языка.

Как и другие системы нечёткого вывода, нечёткие нейронные сети включают следующие этапы: фаззификацию, нечёткий вывод, дефаззификацию.

На рисунке 1 изображена концептуальная схема нечёткой сети сетей. Она включает: входные данные в виде числовых параметров (x1, x2), слой лингвистических термов, отвечающий за фаззификацию, слой нечётких правил, слой нормализации и сумматор, отвечающих за дефаззификацию. Результатом работы нечёткой сети обычно является вероятность принадлежности некоторому нечёткому множеству. При этом иногда нечёткие нейронные сети содержат несколько сумматоров, в таком случае каждый из них рассчитывает вероятность принадлежности к своему нечёткому множеству и возвращает результат y – вероятность принадлежности входных значений соответствующему множеству.

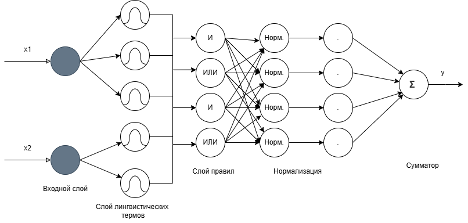
Рисунок 1. Концептуальная схема нечёткой нейронной сети

Входной слой принимает скалярные входные данные и распределяет их по каналам нечёткой системы. Этот слой обычно не содержит параметров и просто передаёт значения входных переменных дальше.

Слой лингвистических переменных отвечает за фаззификацию. На каждом нейроне этого слоя применяется функция принадлежности для каждой входной переменной. Для каждой входной величины определяются степени принадлежности к заданным нечётким множествам (лингвистическим термам): например, входным значением является 1.65, и лингвистические термы для этого входного параметра: «высокая точность», «средняя точность», «низкая точность», тогда после применения функций принадлежности фаззификация помогает  установить, что с силой принадлежности 0.86 входное значение является «высокой точностью», с силой принадлежности 0.44 является «средней точностью» и с силой принадлежности 0.08 является «низкой точностью». Если силы принадлежности нормализовать, то можно получить вероятности, с которыми входное значение принадлежит лингвистическому терму, то есть с какой вероятностью это значение можно назвать соответствующим лингвистическим термом.

В нечётких нейронных сетях в качестве функций принадлежности обычно используются Гауссовы кривые:

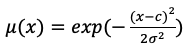                                                                  (1)

где:

μ(x) - значение функции принадлежности,

x - входное значение,

c - центр (аналог среднего в статистике),

σ - ширина (аналог дисперсии),

exp - экспоненциальная функция [4].

Основными параметрами таких кривых являются их центр и ширина, которые могут быть определены для каждого лингвистического терма в процессе обучения сетей.

Слой правил состоит из нейронов типа «И» и «ИЛИ», различающихся своей формулой срабатывания:

• «И» нейрон:

y = max(min(x₁, w₁), min(x₂, w₂), . . . , min(x_n, w_n)),                                            (2)

где:

n  -  количество входов (дендритов),

w₁ - w_n - веса при входах,

x₁ - x_n - параметры на соответствующих входах,

y - результат работы нейрона [2].

• «ИЛИ» нейрон:

y = min(max(x₁, w₁), max(x₂, w₂), . . . , max(x_n, w_n)),                                          (3)

где:

n  -  количество входов (дендритов),

w₁ - w_n - веса при входах,

x₁ - x_n - параметры на соответствующих входах,

y - результат работы нейрона [2].

Здесь происходит вычисление силы срабатывания правила. Предикаты правила комбинируются оператором конъюнкции и/или дизъюнкции.

Слой нормализации преобразует силы срабатывания правил к «вероятностной» форме, деля каждую силу на сумму всех сил.

Сумматор на основе нормализованных сил правил вычисляет вероятность принадлежности к некоторому нечёткому множеству.

Применение нечётких нейронных сетей в сфере профотбора

Нечёткие нейронные сети могут применяться в задаче профессионального отбора для определения по характеристикам кандидата его профпригодности.

По числовым характеристикам кандидата определяется их соответствие: «высоким», «выше среднего», «средним», «ниже среднего», «низким» показателям. И с помощью нечётких правил, созданных на основе обучения на множестве кандидатов с имеющейся оценкой профессиональной деятельности, определяется сложная зависимость характеристик для отбора кандидата и принимается решение о его отношении к множеству подходящих для профессиональной деятельности. Результатом работы будет являться дробное значение от 0 до 1, обозначающее степень профпригодности.

Такая модель обеспечивает интерпретируемость и гибкость принятия решений, особенно в условиях неполной, противоречивой или неточной информации о соискателях. В отличие от классических нейросетей, нечёткие нейронные сети позволяют формализовать экспертные знания в виде нечётких правил, что особенно важно в гуманитарных задачах, где чётких границ между категориями часто не существует. Например, такие характеристики, как «стрессоустойчивость» или «способность к командной работе», не всегда можно оценить строго численно, но они могут быть представлены через лингвистические переменные и обработаны нечёткой логикой.

Кроме того, за счёт встроенного механизма обучения нечёткие нейронные сети способны адаптироваться под конкретные условия профотбора, подстраиваясь под специфические требования работодателя или профессиональной среды. Это делает их особенно полезными в ситуациях, когда профиль идеального кандидата может отличаться в зависимости от корпоративной культуры, задач должности или стратегических целей организации.

Исследование зависимости качества результатов нечётких нейронных сетей от количества правил

Остаётся вопрос о количестве нейронов в слое правил, необходимых для получения наилучшего результата. Для исследования зависимости качества оценки от числа нейронов обучим нечёткие нейронные сети с разным числом нейронов и проведем исследование. В исследовании используются следующие характеристики:

• средняя абсолютная ошибка (MAE).  Показывает среднюю абсолютную ошибку результата от ожидаемого значения:

                                                              (4)

где:

N - количество результатов;

yᵢ - результат i;

ŷᵢ - истинное значение [1, c. 2].

• Robustness (устойчивость к шуму). Позволяет оценить, как сильно результат меняется при добавлении случайных искажений во входные данные:

                                          (5)

где:

MAE_clean - ошибка на чистой выборке;

MAE_noisy - ошибка после зашумления (+10% искажений входных данных) [1, c. 2].

На рисунках 2 и 3 изображены тепловые карты зависимости MAE и Robustness от числа нейронов каждого типа, варьируемого от 2 до 25.

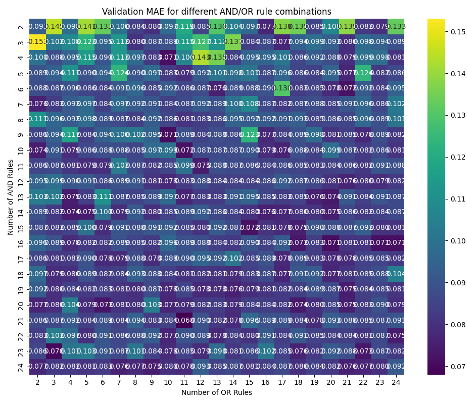
Рисунок 2. Зависимость MAE от количества нейронов

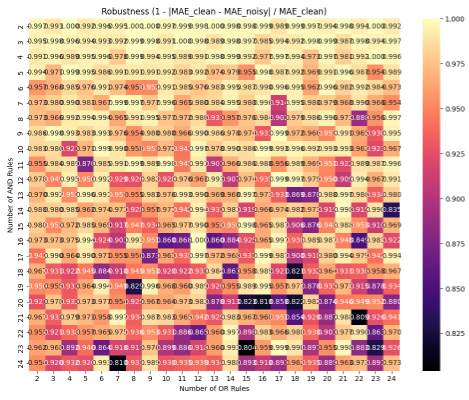
Рисунок 3. Зависимость Robustness от количества нейронов

Из рисунка 2 можно сделать вывод, что для малых значений числа нейронов средняя ошибка больше, чем для больших значений, что объясняется возможностью создания большего количества разрешающих правил при отборе. При этом по рисунку видно, что количество нейронов «И» оказывает большее влияние на ошибку, чем количество нейронов «ИЛИ», что говорит о большей важности правил «И» для задачи профессионального отбора. Можно заметить, что после значения 15 для количества каждого типа нейронов существенного уменьшения ошибки не наблюдается. Это может свидетельствовать о том, что оптимальное количество правил достигнуто. Из рисунка 3 можно сделать вывод, что при дальнейшем росте числа правил будет снижаться устойчивость к шумам в данных.

Заключение

Нечёткие нейронные сети представляют собой эффективный инструмент для решения задач профессионального отбора в условиях неполной или противоречивой информации. Благодаря сочетанию адаптивного обучения и интерпретируемости через нечёткие правила, они позволяют учитывать сложные взаимосвязи между характеристиками кандидатов и требованиями к должности. Эксперимент показал, что увеличение количества нейронов, особенно типа «И», снижает ошибку оценки, однако после определённого порога (~15 нейронов) рост числа правил перестаёт существенно улучшать точность и начинает снижать устойчивость к шумам. Это подтверждает необходимость оптимизации структуры сети для достижения баланса между точностью и надёжностью модели.