ЧАСТОТНОЕ РЕГУЛИРОВАНИЕ ЭЛЕКТРОПРИВОДА. ЗАВИСИМОСТЬ ПРОИЗВОДИТЕЛЬНОСТИ НАСОСА ОТ НАПОРА

Потребление в системе водоснабжения изменяется в зависимости от времени суток, сезона других факторов. Поэтому возникает необходимость регулирования. Одним из методов является частотное регулирование. Плавное изменение параметров системы, встроенные системы защиты, мониторинга и удаленного управления, а также возможность программирования необходимых режимов делают данный метод привлекательным и актуальным в современном мире. Таким образом важной задачей становится определение изменяющихся в ходе регулирования параметров, особенно производительности насоса.

Зависимость напора насоса от его подачи Н=f(Q) называется H-Q или напорно-расходной характеристикой и является одной из наиболее важных характеристик насоса. Она может иметь форму крутой или пологой кривой снижающейся стабильно или лабильной - сперва возрастающей, а потом убывающей. Наиболее эффективно насос эксплуатируется в границах рабочего диапазона, определяемого производителем (как правило 0,7-1,1 от точки оптимальной подачи). В границах рекомендуемых подач и напоров характеристика H = f(Q) описывается уравнением участка квадратичной параболы H_н = Н_ф – S_ф Q_р², где Н_ф — фиктивный напор при нулевой подаче, м; S_ф — гидравлическое фиктивное сопротивление насоса, с²/м⁵. Подобная квадратичная зависимость характеризует и рабочую характеристику сети: H_с = Н_ст + S_в Q_р², где Н_ст - статический напор, м; S_в - гидравлическое фиктивное сопротивление водовода, с²/м⁵.

На основании данных зависимостей выведем формулу для определения рабочей точки системы:

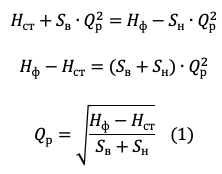
Приняв изменение напора насоса в ходе частотного регулирования за Δz преобразуем приведенные выше формулы:

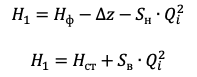
Отсюда подача при изменении напора:

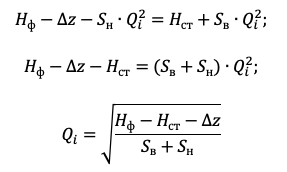
Отношение подачи соответствующей i-му напору системы к расчетной:

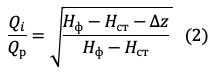
Разница между фиктивным напором насоса и статическим напором системы называется динамической составляющей. Именно в границах этой составляющей возможно регулирование. Поэтому в расчетах по формуле (2) разность Н_ф-Н_ст принимается равной 100%, а изменение напора Δz задается в процентном соотношении относительно неё.

В качестве обоснования применимости формулы (2) и построенного по результатам расчетов графика для систем с различными характеристиками рассмотрим примеры:

Пример 1

Исходные данные:

Кривизна характеристики насоса S_н = 0,001815, фиктивный напор насоса Н_ф = 96,4 м, кривизну характеристики сети S_в = 0,00887, статический напор насоса Н_ст = 0 м

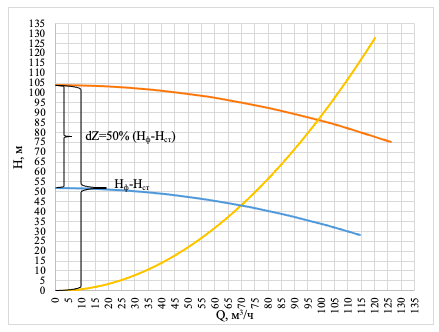
Рис. 2. Рабочая характеристика сети

Расчет исходной подачи по формуле (1):

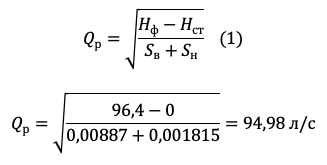
Расчет по формуле (2) при dZ=18,5 м (19,2% от Н_ст-Н_ф):

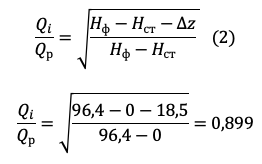
Расчет по формуле (2) при dZ=74 м (76,8% от Н_ст-Н_ф):

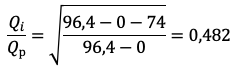
Расчет по формуле (2) при dZ=92,5 м (96% от Н_ст-Н_ф):

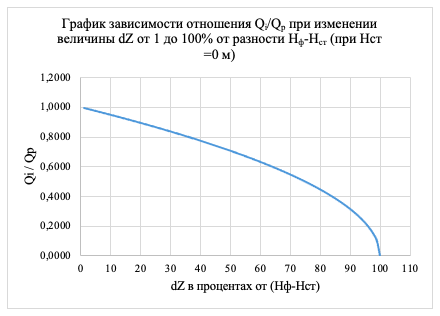
Рис. 3. График зависимости отношения подачи соответствующей i-му напору системы к расчетной при изменении величины dZ от 1 до 100% от разности фиктивного напора насоса и статического напора системы, при Н_ст=0 м

Пример 2

Исходные данные:

Кривизна характеристики насоса S_н = 0,001815, фиктивный напор насоса Н_ф = 96,4 м, кривизна характеристики сети S_в = 0,00287, статический напор насоса Н_ст = 60 м

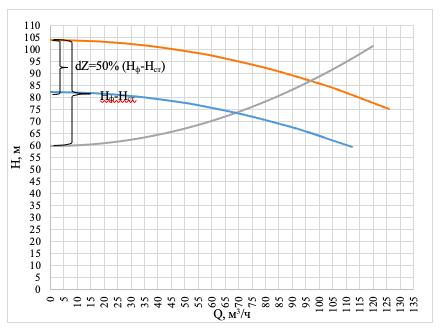
Рис. 4. Рабочая характеристика сети

Расчет исходной подачи по формуле (1):

Расчет по формуле (2) при dZ=6,98 м (19,2% от Н_ст-Н_ф):

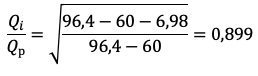
Расчет по формуле (2) при dZ=27,94 м (76,8% от Н_ст-Н_ф):

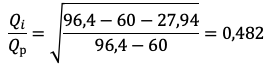
Расчет по формуле (2) при dZ=34,92 м (96% от Н_ст-Н_ф):

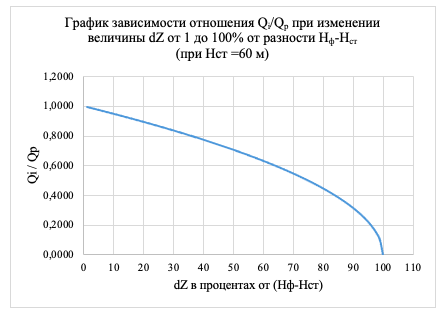
Рис. 5 График зависимости отношения подачи соответствующей i-му напору системы к расчетной при изменении величины dZ от 1 до 100% от разности фиктивного напора насоса и статического напора системы, при Н_ст=60 м

Как видно из приведенных примеров изменение производительности насоса в ходе частотного регулирования подчиняется определенному закону вне зависимости от производительности, напора и прочих параметров и может быть определено из предложенных в данной работе формул и графика.

Выводы

Полученные в ходе данной работы зависимости отражают закон изменения производительности насоса при частотном регулировании вне зависимости от характеристик системы. Все выведенные формулы и построенные по результатам расчета графики показывают достаточную точность в границах рабочего диапазона насоса и могут применяться специалистами для прогнозирования работы насосного оборудования.