Машинное обучение – раздел искусственного интеллекта, изучающий алгоритмы, способные обучаться. Очень распространёнными при решении задач машинного обучения являются нейронные сети. Подход с использованием нейронных заключается в использовании большого набора тренировочных данных и разработке системы (модели), которая сможет обучиться на основе предоставленных тренировочных данных.
Главная задача при обучении нейронной сети сделать так, чтобы обученная модель давала верный или близкий к верному результат на других данные, а не только на тех, которые использовались при тренировке. Эффект, когда нейронная сеть обучается слишком сильно на тренировочных данных и теряет качество на реальных тестовых данных, называется переобучением. Переобучение является одной из основных проблем машинного обучения.
Искусственная нейронная сеть (ИНС) — математическая модель, а также её программное воплощение, построенная по принципу организации и работы биологических нейронных сетей — сетей нервных клеток живого организма.
Скрытые слои представляют структуру обучающего алгоритма. Цель нейронной сети – приблизить некоторою функцию
Вход – вектор столбец 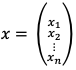 , где n – количество элементов входа. Веса, соединяющие слой l и l+1, задаются матрицей
, где n – количество элементов входа. Веса, соединяющие слой l и l+1, задаются матрицей 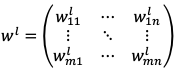 ,
,
где n – количество нейронов слоя l+1; m – количество нейронов слоя l.
То есть ![]() – вес между нейронами i и j слоев l+1 и l соответственно.
– вес между нейронами i и j слоев l+1 и l соответственно.
Смещение слоя l задаёт вектор столбец 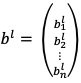 , где n – количество нейронов в слое l. Введем обозначение
, где n – количество нейронов в слое l. Введем обозначение
![]() (1.1)
(1.1)
Общий процесс вычисления значений нейронной сети можно представить в следующем виде:
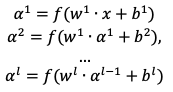 (1.2)
(1.2)
где 𝑔 – некоторая функция, преобразующая один слой в другой. Это может быть, как перцептрон, так и другая функция.
Функция стоимости
Функция стоимости используется при обучении нейронной сети и помогает понять, насколько хорошо обучена сеть. Задача обучения заключается в минимизации функции стоимости.
Одна из наиболее простых функций стоимости (1.3) mean squared error (MSE) или средняя квадратичная ошибка:
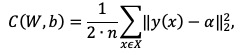 (1.3)
(1.3)
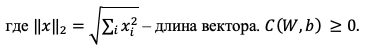
Если результат обучения a близок к значению
Другой пример функции стоимости – функция потерь:
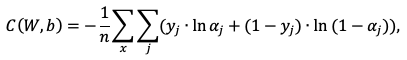 (1.4)
(1.4)
где
Функция активации
Значения нейронов скрытых слоёв вычисляются с помощью некоторой функции. Выбор такой функции сильно влияет на результат сети. Эта функция называется функцией активации, можно сказать, что она активирует (задаёт значение) последующим нейронам. Тренировка сети и проверка на валидационном множестве позволяют выявить результат и выбрать лучший. Одна из наиболее часто используемых функций – сигмоида:
![]() (1.5)
(1.5)
Сигмоида – непрерывная, дифференцируемая, при этом ограничена горизонтальными асимптотами y = 1, y = 0 (рис. 1).
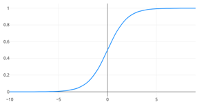
Рисунок 1. Графическое представление сигмоиды
Подходит в случаях, когда необходимо задавать вероятность некоторого события.
Другая функция, похожая на сигмоид – гиперболический тангенс:
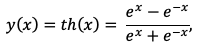 (1.6)
(1.6)
где
Базовые алгоритмы нейронных сетей
Градиентный спуск
Задача обучения нейронной сети – минимизация функции стоимости, т.е. минимизация функции многих переменных. Сперва нужно подсчитать производные первого порядка, решить систему уравнений и найти точки, подозрительные на экстремум. Затем, для того чтобы проверить, какая из точек является локальным минимум, нужно вычислить производные второго порядка.
Рассмотрим алгоритм градиентного спуска. Для простоты вычислений выберем функцию стоимости (1.3).
Пусть наша задача состоит в минимизации функции  мы хотим найти направление, в котором
мы хотим найти направление, в котором ![]() , считая длину вектора постоянной, выражение сведётся к
, считая длину вектора постоянной, выражение сведётся к
Таким образом мы можем уменьшать нашу функцию в направлении обратную градиенту. По следующему правилу:
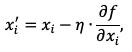 (2.1)
(2.1)
где 𝜂 – learning rate, скорость обучения, положительное число, задающее размер шага, с которым заданная функция уменьшается.
Перенесём (2.1) на функцию стоимости, получим:
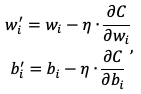 (2.2)
(2.2)
Например, всё множество входных данных  случайно разбивается на несколько подмножеств:
случайно разбивается на несколько подмножеств:
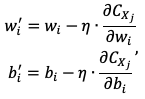 (2.3)
(2.3)
где  - функция, усреднённая по набору
- функция, усреднённая по набору
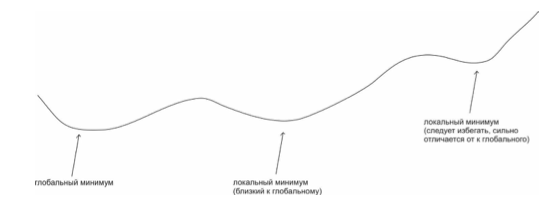
Рисунок 2. Графическое представление функции одной переменной с несколькими минимумами
Если при работе алгоритма градиентного спуска начальное положение значения весов и смещения были выбраны рядом с одним из локальных минимумов, то существует вероятность того, что мы не сможем выбраться из этого локального минимума. И если значение этого локального минимума сильно отличается от глобального, то и результат работы нейронной сети будет далёк от желаемого.
Алгоритм обратного распространения ошибки
В то время, когда алгоритм градиентного спуска служит для минимизации функции, алгоритм обратного распространения ошибки предназначен для быстрого вычисления градиента. Для вычисления градиента необходимо вычислять частные производные ![]() . Вычислять их каждый раз вручную – трудная задача, так как нейронная сеть может быть глубокая и иметь множество параметров. Для быстрого вычисления градиента функции стоимости был придуман алгоритм обратного распространения ошибки. Рассмотрим его далее.
. Вычислять их каждый раз вручную – трудная задача, так как нейронная сеть может быть глубокая и иметь множество параметров. Для быстрого вычисления градиента функции стоимости был придуман алгоритм обратного распространения ошибки. Рассмотрим его далее.
Символом ⊚ будем обозначать операцию Адамара.
Воспользуемся обозначениями (1.2) данными выше. В качестве функции стоимости используем среднюю квадратичную ошибку (1.3), в качестве функции активации – сигмоид (1.5). Введём ошибку нейрона j слоя l:
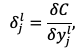 (2.4)
(2.4)
Тогда общий алгоритм будет следующим.
Алгоритм называется обратным распространением ошибки, так как ошибка распространяется назад, на первые слои сети. Мы вычисляем ошибку, начиная с последнего слоя и заканчивая первым. И вычисляем все необходимые параметры нейронной сети за два прохода.
Когда мы используем стохастический градиентный спуск, таких входов несколько. В этом случае мы вычисляем ошибку (2.4) для каждого входа сети. И в конце изменяем веса и смещения по следующему правилу:
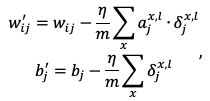 (2.5)
(2.5)
где m – количество элементов в мини батче.
Теперь, когда мы знаем базовые обучающие алгоритмы нейронных сетей, сделаем несколько выводов из полученных знаний.
Сверточные нейронный сети
Свёрточные сети получили такое название, т.к. используют внутри операцию свёртки. Далее будем рассматривать свёрточные нейронные сети применительно к изображениям. Один слой свёрточной нейронной сети лучше воспринимать как квадрат нейронов размером
Свёртка – особый вид интегрального преобразования. Пусть  и
и  – две интегрируемые функции
– две интегрируемые функции
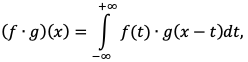 (2.6)
(2.6)
Рассмотрим операцию свёртки на примере. Пусть стоит задача вычислить количество нерастаявшего снега в определённый момент времени. Сложность заключается в том, что во время выпадения нового снега, старый может таять. При этом нам известно  – момент времени, в который мы хотим узнать количество оставшегося снега,
– момент времени, в который мы хотим узнать количество оставшегося снега,  – момент выпадения конкретной порции снега. Необходимо построить функцию
– момент выпадения конкретной порции снега. Необходимо построить функцию
Тогда, например, если нам необходимо найти количество снега в момент времени  , оставшееся от снега выпавшего в момент времени
, оставшееся от снега выпавшего в момент времени
Очень часто данные представляются через определённый временной интервал, например, одна секунда. В этом случае мы работаем с дискретной свёрткой:
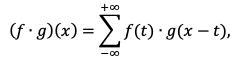 (2.7)
(2.7)
Теперь рассмотрим основные принципы, на которых основаны свёрточные нейронные сети. Затем вернёмся к применению операции свёртки для изображений.
Локальные области
Как и в сетях прямого распространения, мы соединяем нейроны входа с нейронами скрытого слоя. Однако вместо того, чтобы соединять каждый нейрон входа с каждым нейроном скрытого слоя, будем соединять только нейроны из конкретной маленькой области входа с одним нейроном скрытого слоя. При этом каждая связь имеет вес, и нейрон скрытого слоя имеет своё смещение.
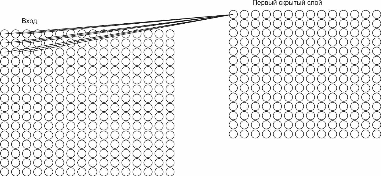
Рисунок 3. Графическое представление связи нейронов локальной области входного изображения
На рис. 3 показаны связи нейронов локальной области входного изображения с одним нейроном скрытого слоя. Здесь размер локальной области равен 3
В терминологии свёрточной сети мы называем результат операции свёртки, т.е. результат отображения входного слоя в скрытый – feature map. Веса и смещения являются общими и вместе называются kernel или filter. Для того, чтобы распознать изображение хорошо, нам необходима больше, чем одна feature map. Поэтому целиком один слой свёрточной нейронной сети состоит из нескольких feature map.
Определим активацию нейрона исходя из данных свойств и рис. 3:
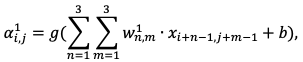 (2.8)
(2.8)
где ![]() ,
,  и m от 1 до 3 – общие веса,
и m от 1 до 3 – общие веса,
Воспользуемся (2.7), где определим функции  и
и  равными 0 на всей области определения кроме конечного множества точек и поскольку мы работаем с изображениями, то вход имеет размерность два. Мы можем переписать (2.7) к виду:
равными 0 на всей области определения кроме конечного множества точек и поскольку мы работаем с изображениями, то вход имеет размерность два. Мы можем переписать (2.7) к виду:
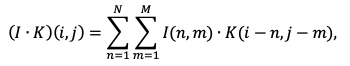 (2.9)
(2.9)
где
l – изображение;
K – kernel.
Тогда (2.8) для в общем виде преобразуется к (2.10):
![]() (2.10)
(2.10)
Тут определена активация для выделения одного свойства. При определении нескольких feature map будет выделено несколько групп общих весов и смещений. Полное представление скрытого слоя свёрточной нейронной сети представлено на рис. 4.
Рисунок 4. Графическое представление скрытого слоя нейронной сети
На данном рисунке для одного входного слоя нейронной сети генерируется 6 feature map. Например, для рис. 5 у нас будет 1960 параметров, против 65 792 для обычной сети. Получаем улучшение почти в 30 раз, что даёт выигрыш в памяти и скорости обучения.
Таким образом, нейронные сети представляют собой мощный инструмент, способный решать широкий спектр задач, начиная от классификации данных и заканчивая обработкой изображений. Их обучение основано на математически строгих алгоритмах, которые обеспечивают точное приближение сложных функций. Выбор правильной архитектуры, функций активации и методов обучения является ключевым шагом в создании эффективной модели.
Список литературы
- Kim, C. Multiple Hypothesis Tracking Revisited / C. Kim, F. Li, A. Ciptadi, J.M. Rehg // International Conference on Computer Vision, 2015. – P. 4696-4704. DOI: 10.1109/ ICCV.2015.533
- Bewley, A. Simple online and realtime tracking / A. Bewley, G. Zongyuan, F. Ramos, B. Upcroft // ICIP. – 2016. – P. 3464-3468
- Wojke, N. Simple online and realtime tracking with a deep association metric / N. Wojke, A. Bewley, D. Paulus // arXiv preprint, 2017. – arXiv:1703.07402



