ГАРМОНИЯ СВЕТИЛ СОЛНЕЧНОЙ СИСТЕМЫ НА ЗЕМНОМ НЕБОСВОДЕ

Введение. С древних времен известно понятие парада планет [1], когда несколько планет Солнечной системы оказываются приблизительно на одной прямой при наблюдении с Земли, что позволяет земному наблюдателю их видеть с небольшим "разбросом" в пределах углового сектора в 25-30 градусов. Также известно, что эти явления бывают исключительно редко (не чаще одного раза в несколько лет) в зависимости от количества одновременно наблюдаемых планет.

Автор решил сосредоточиться на планетах, которые видимы невооруженным глазом с Земли, и добавил к списку Солнце и Луну. В результате в исследование вошли семь ключевых объектов (светил) Солнечной системы: Солнце, Луна, Меркурий, Венера, Марс, Юпитер и Сатурн. Можно предположить, что время от времени эти светила выстраиваются не только в одну линию, создавая парад светил, но и равномерно распределяются по небесному экватору, создавая таким образом гармонию в пространстве на небосводе Земли. Цель данного исследования состоит в том, чтобы с помощью вычислений взаимного расположения светил на небесной сфере выявить уникальные моменты красоты и гармонии природных явлений в космическом пространстве.

Научной основой данного исследования стали расчеты ежедневных геоцентрических координат [2] светил в период 20-го века с 1 января 1900 года по 31 декабря 1999 года, а также в 21-м веке с 1 января 2000 года по 31 декабря 2099 года. Эти расчеты были выполнены с использованием известных алгоритмов [3] с учетом элементов орбит светил точностью не хуже 0.1 углового градуса, чего оказалось вполне достаточно для дальнейшего анализа.

При расчетах и анализе координат светил в экваториальной системе координат автор обратил внимание на эпизодически (исключительно редкую, несмотря на быстрые ежедневные изменения Луны) возникающую необычную видимую с Земли геометрию видимых семи светил Солнечной системы.  Геометрия соответствует определенной эстетически симметричной гармонии в зависимости от определенных критериев. Статью можно считать развитием авторских идей, изложенных ранее в оригинальной работе [4], в которой было обращено внимание на различные экстремальные расположения планет Солнечной системы на эклиптике.

Теоретическое обоснование. Рассмотрим небесную сферу, с центром, связанным с земным наблюдателем и с расположенными практически в плоскости эклиптики светилами. На небосводе Земли семь светил Солнечной системы (рис. 1) выстраиваются в наблюдаемую на небесной сфере линию (по кругу) в различной конфигурации друг относительно друга. Наибольший интерес представляют вычисленные углы, называемые прямыми восхождениями светил относительно направления на точку весеннего равноденствия ϒ (точку Овна) против часовой стрелки, если смотреть с Северного полюса мира. Координаты светил на небесной сфере постоянно изменяются с течением времени, что и приводит к различной наблюдаемой геометрии. Главным образом, это касается значений координат прямого восхождения. Например, Солнце описывает по прямому восхождению полный круг в течение одного года, Луна – в течение ~28 дней. Для планет подобные периоды составляют: Меркурий ~ 1 год, Венера ~ 300-400 дней, Марс ~ 710 дней, Юпитер ~ 12 лет и Сатурн ~ 29 лет. Можно сказать, что из-за существенной разности периодов и складывается причудливая мозаика всей картины небесной сферы.

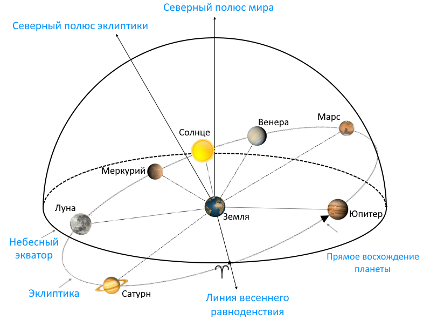
Рисунок 1. Схематичное расположение светил на небесной сфере

Назовем симметричной гармонией светил небесной сферы такое их расположение, при котором они распределены равномерно по кругу небесной сферы. Это означает, что прямые восхождения углов каждого светила с двумя соседними составляют ровно 1/7 полной окружности (рис. 2), т.е. примерно 51 градус. В данном случае не учитывается порядок расположения светил. Это позволяет говорить об абсолютной геометрической, осевой, поворотной, зеркальной и вращательной симметрии [5]. Другим, не менее значимым событием для геометрии светил, является их размещение в узком угловом секторе на небесной сфере, который и назовем парадом светил (не планет) в дальнейшем показанным на рисунках.

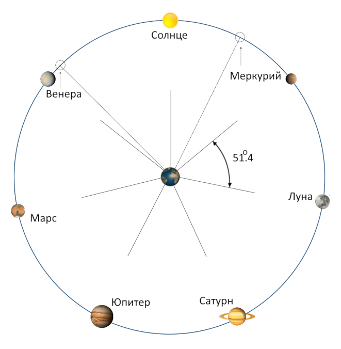
Рисунок 2. Расположение видимых светил в случае симметричной гармонии небесной сферы для земного наблюдателя

Такое положение планет, образующих правильный семиугольник, является теоретическим и принципиально недостижимым практически хотя бы потому, что предельно возможный угол наблюдения с Земли между Солнцем и Меркурием не может превышать 28 градусов, а между Солнцем и Венерой - 48 градусов. Эти предельные положения двух внутренних схематично планет показаны пунктиром на рисунке 2. Поэтому симметрию или гармонию светил на практике будут характеризовать параметры приближения расположения светил к абсолютной симметрии семиугольника, для которой и определим критерии приближения по авторскому алгоритму расчета критериев, исходя из соображений отличия углов между светилами от идеальных.

Итак, имеем в качестве исходных данных массив прямых восхождений αi (i=1,2,3,4,5,6,7) на любую заданную в течение 20-го и 21-ого веков (всего 73050 дней), выраженных в угловых градусах, всех видимых с Земли 7-ми ярких светил. Вычисления осуществляем в следующей последовательности:

- сортируем массив значений αi по возрастанию, переопределяя индексы светил в соответствии с параметрами сортировки;

- вычисляем последовательные (вдоль небесного экватора) геоцентрические углы ∆α между соседними светилами

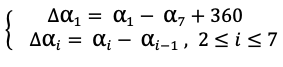                                                                 (1)

- вычисляем значение среднеквадратического отклонения (в угловых градусах) полученных на предыдущем этапе 7-ми значений углов на любую заданную дату от идеального угла в 51.4 градуса

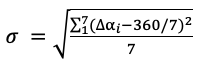                                                                 (2)

По сути, параметр сигма (σ) из уравнения (2) с размерностью в угловых градусах является критерием гармонии расположения светил.

Система стремится к симметричной гармонии, когда все светила идеально расположены в вершинах семиугольника, при

                                                                            (3)

Если же теоретически все светила расположены по направлению от земного наблюдателя в одну сторону на одной прямой, то можно сказать, что система стремится к параду светил, при этом параметр  сигма (σ) оценивается формулой

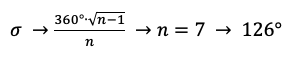                                                       (4)

Результаты вычислений и анализ положений светил. По приведенному алгоритму вычислены и отображены на графике 1 все значения сигма (σ) критериев гармонии на каждый день в течение 20-го и 21-го веков или за 73050 дней.

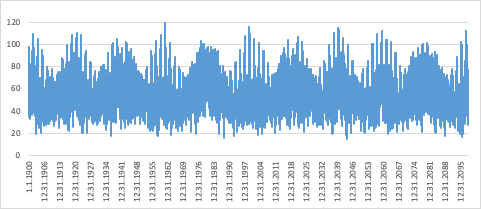
График 1. Зависимость значений критерия гармонии

Из графика 1 видно, что параметр сигма (σ) практически лежит в диапазоне от 14º до 120º угловых градусов. Причем верхний предел, который соответствовал экстремальному положению парада светил за весь двухвековой период был достигнут 05.02.1962 и равнялся при значении σ = 119º.28, а все светила при этом собирались в наиболее узком секторе равным 27º. Нижний же предел, соответствующий максимально симметричному расположению светил на небесном экваторе за весь двухвековой период будет достигнут только 17.07.1944 при значении σ = 14º.55. Заметим, что в отличие от нижних пределов, верхние укладываются в достаточно периодическую структуру с интервалом порядка 20 лет. А у нижних пределов подобной структуры не наблюдается, т.е. симметричное (гармоничное) расположение светил носит более хаотичный характер во времени.

Проиллюстрируем на рисунке 3 расположение светил на земном небосводе в момент их “наилучшего” парада, воспользовавшись здесь и в дальнейшем возможностями ресурса Stellarium [6], в азимутальной проекции звездного неба. Размеры светил показаны исключительно из-за их узнаваемости и на всякий случай расшифрованы на рисунке 4. Видно, что светила располагаются практически на одной линии с Солнцем и не могут быть доступны земному наблюдателю, разве что только во время солнечного затмения,  тем не менее программа Stellarium позволяет их “увидеть” на фоне звездного неба.

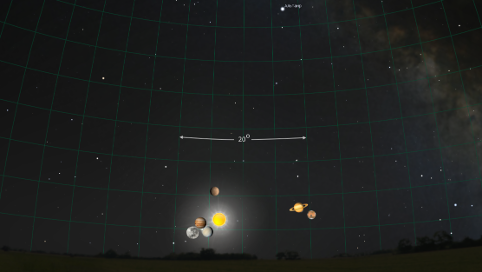
Рисунок 3. Парад видимых светил Солнечной системы 07 июля 2044 года

Рисунок 4. Обозначения 7-ми видимых светил Солнечной системы

На рисунке 5 проиллюстрируем расположение светил на земном небосводе в момент их наиболее симметрично-гармоничного расположения в стереографической проекции звездного неба, что очень близко к правильному семиугольнику

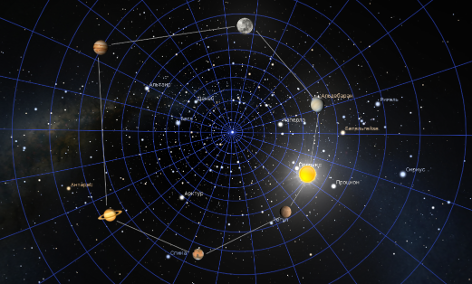
Рисунок 5. Гармония видимых светил Солнечной системы 05 февраля 1962 года

Поскольку экстремальные положения светил, как следует из графика 1, могут встречаться многократно, хоть и не так часто, как могло бы быть, то определим критерии подобных положений. Для этого применим оригинальный способ, который состоит в том, что сначала располагаем по сортировке значений параметров сигма (σ) от большего к меньшему (или наоборот), после чего получаем график 2 всех отсортированных значений

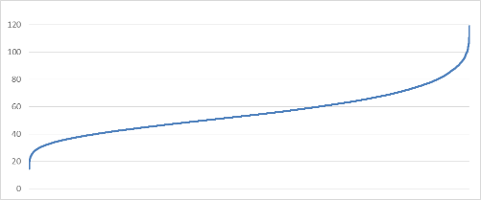
График 2. Кривая изменения критерия сигма (σ) по сортировке значений

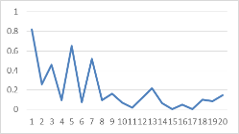
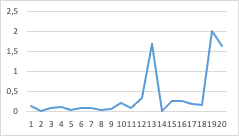
На концах кривой видны существенные изгибы (переломы на кривой), математически характеризующиеся быстрым изменением первых разностей или производных. Именно по ним и найдем критерии, рассмотрев более подробно поведение производных кривой графика на ее концах. Для этого построим графики первых разностей (производных) на обоих концах кривой, эмпирически взяв в расчеты по 20 дат-точек       

                                                 

График 3а. Для определения  критерия гармонии светил

График 3б. Для определения критерия парада светил

 

Из анализа графика 3а критерий гармонии (симметрии) светил лежит в области 7-ой точки с начала со значением σ = 17.43, а из анализа графика 3б критерий парада светил лежит также в области 7-ой точки с конца со значением σ = 114.71.

Таким образом, определим даты, которые соответствуют пределам вычисленных параметров сигма (σ) и отобразим их в таблицах 1 и 2.

Таблица 1.

Положения светил в хронологическом порядке в моменты симметричной гармонии при σ < 17.43

Дата	Сигма (σº)
23.09.1988	15.63
05.06.1993	16.91
17.07.2044	17.43
22.01.2097	16.84

 

Таблица 2.

Положения светил в хронологическом порядке в моменты их парадов при σ > 114.71

Дата	Сигма (σº)
05.02.1962	119.28
04.05.2000	115.28
07.09.2040	114.71

        

Безусловно, есть и другие даты с положениями светил близкими или далекими по отношению к экстремальным, которые здесь не отображены из-за ограничений объема статьи. Для каждой группы принципиально можно рассчитать диапазоны и критерии к ним аналогично работе [4]. Тем не менее, одно из них добавим. Поскольку рисунки светил в их экстремальных положениях были приведены выше, дополнительно отобразим на рисунке 6 некоторое среднее положение или обычное, чаще всего встречающееся на протяжении двух веков, отличное от экстремального, например, в периоде подготовки статьи в начале октября 2024 года. Расположение светил достаточно отдаленно напоминает правильный семиугольник.

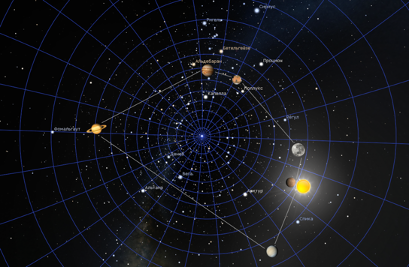
Рисунок 6. Положение светил на 01.10.2024 σ = 42.99

На рисунках 5 и 6 хорошо заметны отличия гармоничного расположения светил Солнечной системы от стандартного “обычного”.

Заключение и выводы. Работа завершает цикл из 5-ти статей, демонстрирующих оригинальный переход к изучению геометрии Солнечной системы с вычислением новых динамически экстремальных геометрических расположений планет и светил друг относительно друга в любой момент прошлого, настоящего и будущего времени в течение 20-го и 21-го веков для гипотетического наблюдателя на небосводе Солнца и небосводе Земли. Концептуально были введены и обоснованы понятия одиночества планет Солнечной системы [7-9], а также гармонии или дисгармонии их расположения на эклиптике [4] и на небесной сфере.

В заключение серии статей о планетах и светилах Солнечной системы,  представим в виде таблицы 3 сводную информацию о предстоящих интересных явлениях, ожидаемых в ближайшие 25 лет, вплоть до 2050 года.

Таблица 3.

Ожидаемые явления в Солнечной системе до 2050 года

Дата	Описание явления	Небесный круг	Планета / Группа Светил	Ссылка на статью
31.08.2025	Одинокая планета	Эклиптика	Марс	[8]
06.05.2026	Одинокая планета	Эклиптика	Земля	[7]
27.09.2026	Одинокая планета	Эклиптика	Меркурий	[8]
14.12.2026	Одинокая планета	Эклиптика	Меркурий	[8]
26.10.2027	Одинокая планета	Эклиптика	Юпитер	[9]
10.03.2028	Одинокая планета	Эклиптика	Меркурий	[8]
17.07.2028	Одинокая планета	Эклиптика	Юпитер	[9]
08.09.2028	Одинокая планета	Эклиптика	Юпитер	[9]
08.12.2029	Одинокая планета	Эклиптика	Юпитер	[9]
30.08.2030	Одинокая планета	Эклиптика	Юпитер	[9]
24.09.2031	Одинокая планета	Эклиптика	Меркурий	[8]
12.09.2033	Одинокая планета	Эклиптика	Меркурий	[8]
01.05.2034	Одинокая планета	Эклиптика	Земля	[7]
18.10.2035	Одинокая планета	Эклиптика	Венера	[8]
11.01.2036	Сильная дисгармония	Эклиптика	Меркурий - Венера - Земля - Марс - Юпитер - Сатурн - Уран - Нептун	[4]
08.02.2036	Одинокая планета	Эклиптика	Меркурий	[8]
28.10.2037	Одинокая планета	Эклиптика	Меркурий	[8]
20.01.2038	Одинокая планета	Эклиптика	Меркурий	[8]
19.06.2038	Одинокая планета	Эклиптика	Земля	[7]
15.02.2039	Одинокая планета	Эклиптика	Марс	[8]
09.10.2039	Одинокая планета	Эклиптика	Меркурий	[8]
07.01.2040	Одинокая планета	Эклиптика	Меркурий	[8]
25.02.2040	Одинокая планета	Эклиптика	Венера	[8]
07.09.2040	Парад светил	Земной экватор	Солнце - Луна - Меркурий - Венера - Марс - Юпитер - Сатурн	Текущая
29.01.2041	Одинокая планета	Эклиптика	Марс	[8]
15.02.2041	Одинокая планета	Эклиптика	Нептун	[9]
14.05.2042	Одинокая планета	Эклиптика	Нептун	[9]
17.07.2042	Одинокая планета	Эклиптика	Нептун	[9]
25.03.2044	Одинокая планета	Эклиптика	Нептун	[9]
21.06.2044	Одинокая планета	Эклиптика	Нептун	[9]
17.07.2044	Симметричная гармония	Земной экватор	Солнце - Луна - Меркурий - Венера - Марс - Юпитер - Сатурн	Текущая
29.08.2044	Одинокая планета	Эклиптика	Уран	[9]
29.09.2044	Совершенная гармония	Эклиптика	Меркурий - Венера - Земля - Марс - Юпитер - Сатурн - Уран - Нептун	[4]
01.12.2045	Одинокая планета	Эклиптика	Сатурн	[9]
11.07.2046	Одинокая планета	Эклиптика	Уран	[9]
16.02.2047	Одинокая планета	Эклиптика	Сатурн	[9]
07.11.2047	Одинокая планета	Эклиптика	Сатурн	[9]
21.01.2049	Одинокая планета	Эклиптика	Сатурн	[9]
31.03.2049	Одинокая планета	Эклиптика	Сатурн	[9]
20.10.2049	Одинокая планета	Эклиптика	Сатурн	[9]
28.12.2050	Одинокая планета	Эклиптика	Сатурн	[9]

 

Результаты исследований могут привлечь внимание не только астрономов и экспертов по небесной механике, но (вполне возможно) и астрологов. С одной стороны, специалисты обращают внимание на геометрические соотношения между планетами Солнечной системы, с другой - автор не сталкивался с использованием или интерпретацией, описанных в цикле пяти оригинальных статей, небесных геометрических явлений в подобном контексте и при таких конфигурациях объектов Солнечной системы.