Введение. При расчетах и анализе гелиоцентрических долгот [1] планет за период 20-го и 21-го веков автор обратил внимание на эпизодически возникающую необычную геометрию планет Солнечной системы, если рассматривать положение планет друг относительно друга на линии эклиптики [2], т.е. практически на небосводе Солнца. Геометрия положения планет соответствует диапазону от практически или эстетически симметричной гармонии до асимметричной дисгармонии в зависимости от определенных критериев. Статью можно считать развитием авторских идей, изложенных ранее в оригинальной работе [3], в которой было обращено внимание на эклиптически экстремальные расположения Земли относительно других планет.
Различное в любой момент времени геометрическое расположение планет оказывает влияние на многие параметры Солнечной системы [4]. Результаты работы могут быть применимы для анализа и поиска решения значимых научно-практических задач астрономии в части уточнения возмущающих гравитационных параметров орбит планет. Не исключена и взаимозависимость многих земных природных и других факторов от экстремальных конфигураций планет, о которых идет речь в работе.
Теоретическое обоснование. Рассмотрим плоскость эклиптики. образующей на небесной сфере большой круг, наклоненный к плоскости небесного экватора в настоящую эпоху на угол 23o26’. Если наблюдателю гипотетически расположиться в центре Солнца – центре гелиоцентрической системы координат, то можно в одной плоскости (эклиптики) наблюдать все восемь планет Солнечной системы (рис. 1), которые выстраиваются в наблюдаемую линию (по кругу) в различной конфигурации друг относительно друга.
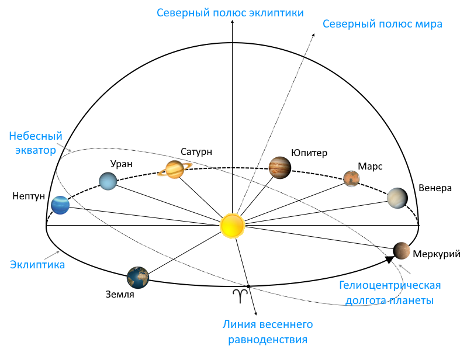
Рисунок 1. Расположение планет на эклиптике
Углы планет отсчитываются от точки весеннего равноденствия ϒ (точки Овна) против часовой стрелки (если смотреть из северного полюса эклиптики) и называются гелиоцентрическими долготами, которые рассчитываются по известному алгоритму [5], основанному на использовании таблиц кеплеровских параметров орбит планет на заданную эпоху и решения итерационным методом кеплеровского уравнения для расчета значения эксцентрической аномалии (для краткости опустим здесь достаточно громоздкий алгоритм вычислений).
По формулам алгоритма автором были произведены вычисления гелиоцентрических долгот всех планет (Меркурия, Венеры, Земли, Марса, Юпитера, Сатурна, Урана и Нептуна) Солнечной Системы на каждый день за период 20-го века (01.01.1900 – 31.12.1999) и за весь период 21-го века (01.01.2000 – 31.12.2099).
Назовем абсолютно симметричной гармонией эклиптики такое расположение планет, при котором они распределены равномерно по кругу эклиптики. Это означает, что гелиоцентрические разности углов каждой планеты с двумя соседними составляют ровно 45° (рис. 2). В этом случае последовательность расположения планет в расчет не принимается. Тогда можно говорить об абсолютной геометрической, осевой, поворотной, зеркальной, вращательной симметрии [6].
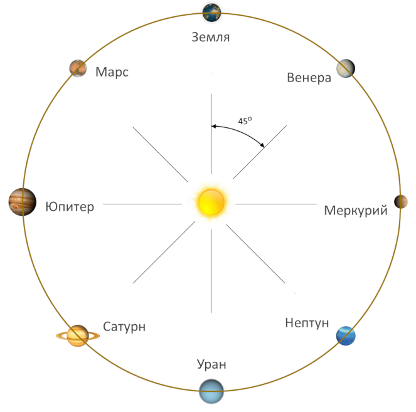
Рисунок 2. Расположение планет в случае абсолютной
симметричной гармонии
Такое положение планет, образующих правильный восьмиугольник, является чисто теоретическим и недостижимо практически. Поэтому гармонию эклиптики на практике будут характеризовать параметры приближения расположения планет к абсолютной симметрии, для которой определим критерии приближения по авторскому алгоритму расчета критериев, исходя из соображений отличия углов между планетами от идеальных. Пусть имеем на заданную дату массив гелиоцентрических долгот Li (i=1,2,3,4,5,6,7,8), выраженных в угловых градусах, всех 8-ми планет. Тогда, алгоритм следующий:
- сортируем массив значений Li по возрастанию, переопределяя индексы планет в соответствии с параметрами сортировки;
- вычисляем последовательные (вдоль эклиптики) гелиоцентрические углы ∆L между соседними планетами
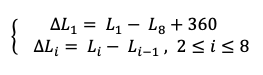
(1)
- вычисляем значение среднеквадратического отклонения (в угловых градусах) полученных на предыдущем этапе 8-ми значений углов на любую заданную дату от идеального угла в 45 градусов
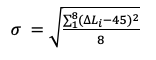
(2)
По сути, параметр сигма (σ) из уравнения (2) с размерностью в угловых градусах является критерием гармонии расположения планет.
Система стремится к симметричной гармонии, когда
![]()
(3)
Система стремится к антисимметричной дисгармонии, когда
![]()
(4)
По приведенному алгоритму вычислены и отображены на графике 3 все значения сигма (σ) критериев гармонии на каждый день в течение 20-го и 21-го веков или за 73050 дней.
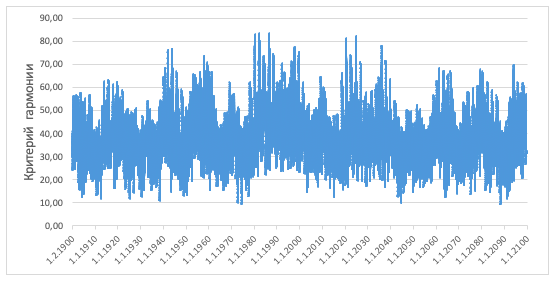
График 1. Зависимость значений критерия гармонии в рамках диапазона дат
Из графика 1 видно, что параметр сигма (σ) практически лежит в диапазоне от 10º до 85º угловых градусов. Причем значения параметра гармонии менее 10º или более 80º на протяжении двух столетий встречается лишь несколько раз, достигая минимального предела
![]()
(5)
Поскольку такое идеальное положение планет - дело далекого будущего, определим дату наиболее близкого к нему положения по критерию сигма (σ). Оказывается, что такая дата была в недалеком прошлом
![]()
(6)
Гармоничное расположение планет на эклиптике в случае экстремальных положений иллюстрируют рисунки 2а и 2б.
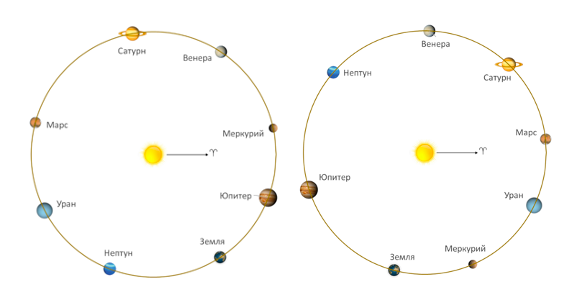
|
Рисунок 2а. Совершенная гармония. Положение планет 26 июля 1974 года |
Рисунок 2б. Совершенная гармония Положение планет 06 июня 2088 года |
Действительно, выбранные критерии достаточно точно относят выбранные даты к гармоничному расположению планет.
Как было отмечено выше, расположение планет экстремально может приводить не только к гармонии, но и к дисгармонии, т.е. к асимметричному расположению планет. Отметим, что наибольшее значение, относящееся к дисгармонии, осталось в недалеком прошлом
![]()
(7)
А вот очень близкое по значению аналогичное событие предстоит в ближайшем будущем
![]()
(8)
Также покажем на рисунках 3а и 3б дисгармоничное (асимметричное) положение планет, даты которых точно соответствуют вычисленным критериям сигма (σ)
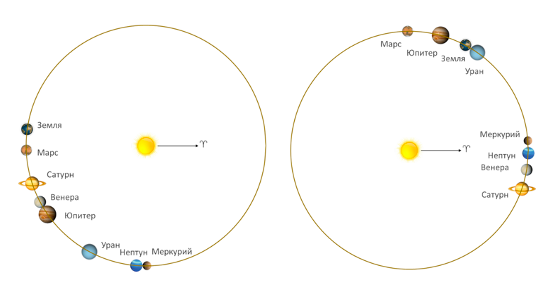
|
Рисунок 3а. Сильная дисгармония. Положение планет 11 марта 1982 года |
Рисунок 3б. Сильная дисгармония. Положение планет 23 ноября 2024 года |
На рисунках 2 и 3 показаны экстремальные гармоничные и дисгармоничные (симметричные и асимметричные соответственно) положения планет.
Другие положения планет можно считать промежуточными. Поэтому введем понятие градации критерия гармонии/дисгармонии. Для этого применим оригинальный способ, который состоит в том, что сначала располагаем по сортировке значений параметров сигма (σ) от большего к меньшему (или наоборот), после чего получаем график всех отсортированных значений
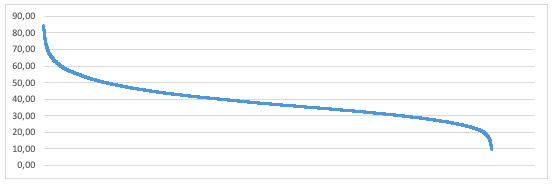
График 2. Кривая изменения критерия сигма (σ) по сортировке значений
На концах кривой видны существенные изгибы (переломы на кривой), математически характеризующиеся быстрым изменением первых разностей или производных. Именно по ним и определим градации критериев, рассмотрев более подробно поведение общей кривой графика на ее концах.
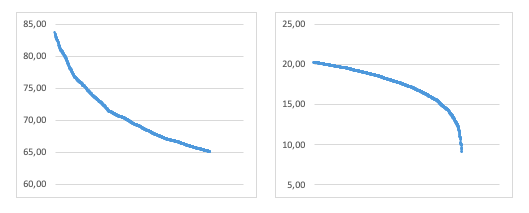
|
График 3а. Для определения градации критерия дисгармонии |
График 3б. Для определения градации критерия гармонии |
Из анализа графика 3б градация критериев гармонии (симметрии) для различных значений сигма (σ) определена в таблице 1:
Таблица 1
|
Название градации критерия гармонии |
Диапазон значений сигма (σº) |
|
Совершенная гармония |
σ < 10 |
|
Сильная гармония |
10 < σ < 12 |
|
Средняя и слабая гармония |
12 < σ < 15 |
|
Неопределенная гармония |
15 < σ < 45 |
Аналогичным образом определим в таблице 2 градацию критериев дисгармонии (асимметрии) для различных значений сигма (σ):
Таблица 2
Градации критерия дисгармонии
|
Название градации критерия дисгармонии |
Диапазон значений сигма (σº) |
|
Сильная дисгармония |
σ > 80 |
|
Средняя дисгармония |
75 < σ < 80 |
|
Слабая дисгармония |
70 < σ < 75 |
|
Неопределенная дисгармония |
45 < σ < 70 |
Продемонстрируем в таблицах и рисунках некоторые результаты касательно симметричной гармонии планет согласно полученным данным в таблице 1.
В таблицах 3, 4 и 5 отображены все даты за весь исследуемый период по градациям гармонии и соответствующим датам значения сигмы (σ)
Таблица 3
Даты совершенной гармонии
|
Дата |
Сигма (σº) |
|
08.09.1972 |
9.96 |
|
26.07.1974 |
9.50 |
|
29.09.2044 |
9.86 |
|
06.06.2088 |
9.06 |
Таблица 4
Даты сильной гармонии
|
Дата |
Сигма (σº) |
|
26.09.1912 |
11.69 |
|
16.03.1925 |
11.83 |
|
16.05.1938 |
10.79 |
|
07.09.1972 |
10.00 |
|
30.09.2044 |
10.15 |
|
03.06.2088 |
10.55 |
|
25.05.2091 |
11.81 |
Таблица 5
Даты средней и слабой гармонии
|
Дата |
Сигма (σº) |
Дата |
Сигма (σº) |
|
22.04.1904 |
12.11 |
15.07.1977 |
12.51 |
|
29.01.1905 |
13.53 |
28.03.2003 |
14.27 |
|
21.08.1910 |
13.20 |
20.03.2015 |
12.35 |
|
18.03.1911 |
13.69 |
30.03.2043 |
12.71 |
|
24.09.1912 |
12.62 |
08.09.2043 |
13.00 |
|
02.12.1924 |
14.42 |
24.09.2044 |
14.21 |
|
15.03.1925 |
12.11 |
18.09.2045 |
14.21 |
|
21.12.1926 |
14.45 |
10.12.2049 |
14.45 |
|
05.08.1930 |
12.67 |
22.02.2064 |
12.23 |
|
12.05.1938 |
12.09 |
12.04.2069 |
13.94 |
|
03.07.1943 |
14.60 |
07.04.2075 |
13.50 |
|
16.01.1949 |
13.16 |
18.10.2083 |
14.28 |
|
23.11.1949 |
14.34 |
14.01.2088 |
14.32 |
|
15.07.1950 |
13.12 |
01.06.2088 |
12.42 |
|
10.09.1972 |
12.16 |
24.05.2091 |
12.27 |
|
30.07.1974 |
12.37 |
09.06.2092 |
14.90 |
В качестве иллюстрации на рисунках 4а и 4б дополнительно показано расположение планет для ближайших в прошлом дат по градациям сильной и слабой / средней гармонии
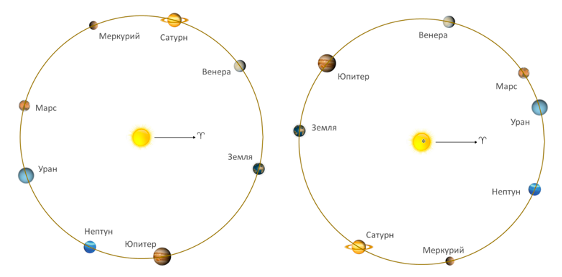
|
Рисунок 4а. Сильная гармония. Положение планет 07 сентября 1972 года |
Рисунок 4б. Средняя (слабая) гармония. Положение планет 20 марта 2015 года |
Продемонстрируем также в таблицах и рисунках некоторые результаты касательно асимметричной дисгармонии планет согласно полученным данным в таблице 2.
Таблица 6
Даты сильной дисгармонии
|
Дата |
Сигма (σº) |
|
12.06.1980 |
82.89 |
|
11.03.1982 |
83.60 |
|
04.08.1986 |
83.31 |
|
21.07.2020 |
81.10 |
|
23.11.2024 |
82.08 |
Таблица 7
Даты средней дисгармонии
|
Дата |
Сигма (σº) |
|
31.01.1942 |
75.96 |
|
08.01.1944 |
76.62 |
|
31.05.1980 |
79.66 |
|
16.03.1982 |
79.96 |
|
25.07.1986 |
79.96 |
|
17.11.1997 |
77.46 |
|
23.10.1999 |
75.36 |
|
12.07.2020 |
79.86 |
|
02.12.2024 |
79.86 |
|
11.01.2036 |
77.99 |
Таблица 8
Даты слабой дисгармонии
|
Дата |
Сигма (σº) |
Дата |
Сигма (σº) |
|
06.02.1942 |
74.99 |
29.06.2020 |
74.00 |
|
31.12.1943 |
70.47 |
05.07.2022 |
73.86 |
|
11.01.1944 |
74.51 |
14.11.2024 |
73.84 |
|
30.01.1958 |
73.50 |
15.11.2026 |
70.78 |
|
26.04.1959 |
70.79 |
31.12.2035 |
71.70 |
|
27.06.1980 |
74.76 |
16.01.2036 |
74.82 |
|
23.03.1982 |
74.86 |
14.12.2037 |
71.36 |
|
14.02.1984 |
73.50 |
|
|
|
08.10.1986 |
74.83 |
|
|
|
20.06.1988 |
74.53 |
|
|
|
21.03.1992 |
70.30 |
|
|
|
03.07.1996 |
71.47 |
|
|
|
31.08.1997 |
74.92 |
|
|
|
24.10.1999 |
74.89 |
|
|
В качестве иллюстрации на рисунках 5а и 5б дополнительно показано расположение планет для ближайших дат по градациям средней и слабой гармонии
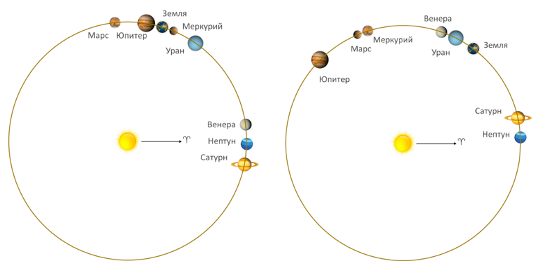
|
Рисунок 5а. Средняя дисгармония. Положение планет 02 декабря 2024 года |
Рисунок 5б. Слабая дисгармония. Положение планет 15 ноября 2026 года |
Наконец, покажем для иллюстрации (рисунок 6) положение планет в момент неопределенной гармонии или дисгармонии, например, на дату начала написания работы:
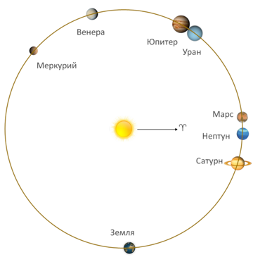
Рисунок 6. Неопределенная гармония/дисгармония.
Сигма (σ) = 46.10 / Июнь 2024 года
Заключение и выводы. Вызывает несомненный интерес оригинальный переход к изучению геометрии Солнечной системы в плоскость эклиптики с вычислением новых динамически экстремальных геометрических расположений планет в любой момент прошлого, настоящего и будущего времени в течение 20-го и 21-го веков для гипотетического наблюдателя на небосводе Солнца. В работе изучены состояния при различных геометрических положениях планет Солнечной системы на линии эклиптики, видимые на небосводе Солнца гипотетическим наблюдателем. Введены понятия симметричной гармонии и асимметричной дисгармонии положений планет, для которых определены различные градации гармоничного и дисгармоничного положения планет в течение 20-го и 21-го веков. Разработаны алгоритмы расчетов. Показано, что гармония эклиптики практически проявляется хоть и не часто, но при этом наблюдается достаточно равномерное распределение гармоничных положений планет вдоль исследуемой оси времени. Важно также отметить, что дисгармоничность эклиптики практически заканчивается в 20-ых - 30-ых годах 21-го века. Исследования в заданном направлении имеют определенную научную ценность, т. к. для рассчитанных положений могут быть уточнены гравитационные составляющие и другие параметры Солнечной системы.
Список литературы
- М. Шевченко, О. Угольников. Астрономический календарь 2023/2024. Серия ‘Как наблюдать за звездами’. Выпуск74. Москва. Издательство АСТ, 2023, С.87. ISBN 978-5-17-154844-5
- Кононович Э.В., Мороз В.И. Общий курс астрономии. — 2-е, исправленное. — УРСС, 2004. — С. 26—30. — 544 с. — ISBN 5-354-00866-2
- В.Г. Соловьев Одинокая планета. Часть 1. Земля. Международный научный журнал “Научный лидер”, №169 / Май 2024, с.27-31. ISSN 2713-3168
- Рой, А. Э. (1988). Орбитальное движение (3-е изд.). Издательство Института физики. ISBN 0-85274-229-0
- Е. Майлс Стэндиш, Джеймс Г. Вильямс. Орбитальные эфемериды Солнца, Луны и планет. [Электронный ресурс]. Режим доступа: https://vadimchazov.narod.ru/text_htm/xsru10.htm (дата обращения 30.06.2024)
- П.С. Моденов, А.С. Пархоменко. Геометрические преобразования. Издательство московского университета. 1961



