ОДИНОКАЯ ПЛАНЕТА. ЧАСТЬ 1. ЗЕМЛЯ

Введение. Представим небесную сферу в гелиоцентрической системе координат [1], в которой наблюдатель гипотетически расположен в ее центре – центре Солнца. Для расчета гелиоцентрических долгот планет, т.е. углов между направлением из центра Солнца на точку весеннего равноденствия и направлением на планету, на любую дату применяется известный алгоритм [2], основанный на использовании таблиц кеплеровских параметров орбит планет на заданную эпоху и решения итерационным методом кеплеровского уравнения для расчета значения эксцентрической аномалии (для краткости опустим здесь достаточно громоздкий алгоритм вычислений).

По формулам алгоритма были произведены вычисления долгот всех планет (Меркурия, Венеры, Земли, Марса, Юпитера, Сатурна, Урана и Нептуна) Солнечной Системы на каждый день за период 20-го века (01.01.1900 – 31.12.1999) и за период 21-го века (01.01.2000 – 31.12.2099).

Теоретическое обоснование и анализ. Проведенные расчеты показали, что в геометрических построениях Солнечной Системы случаются очень редкие моменты времени (всего несколько раз в 100 лет), когда одна из Планет, причем любая из 8-ми, рано или поздно оказывается в положении “одинокой” во время относительно небольшого периода от нескольких дней до нескольких недель.

Дадим определение одиночества Планеты: “Планета считается одинокой в том случае, когда она и только она расположена в передней гелиоцентрической полусфере, построенной относительно линии условного наблюдателя, Солнце-Планета, при этом остальные планеты расположены в задней по отношению к линии условного наблюдателя Солнце-Планета гелиоцентрической полусфере”.

Это означает, что на небосводе Солнца (рисунок 1) минимальные углы между направлением на одинокую Планету (на примере Земли), находящейся в своей полусфере в единственном числе, и направлениями от нее по часовой и против часовой стрелок до ближайших планет (1-ый и 2-ой секторы) соответственно должны быть более 90 градусов каждый. Тогда остальные планеты собраны в одну или несколько групп в рамках ограниченного 180-тью градусами сектора планет противоположной полусферы.

 

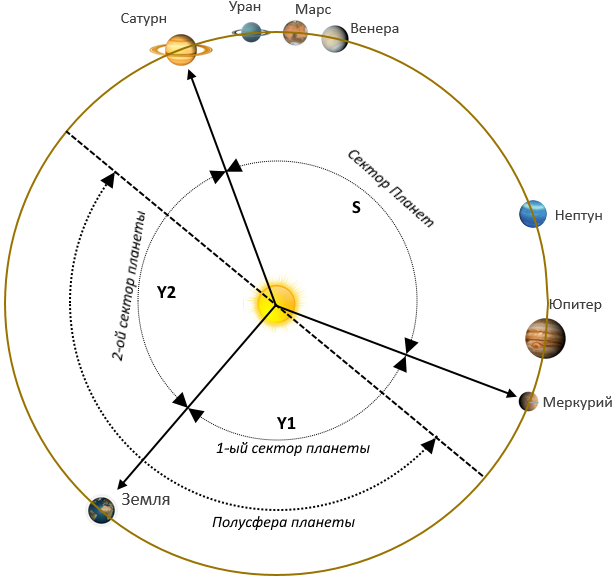
Рисунок 1. Схема расположения планет Солнечной системы для случая одинокой планеты

 

Расчет положений одиночества Планеты осуществляется по следующему алгоритму:

• вычисляются разности (всего таких разностей 7) гелиоцентрических долгот планет Li и гелиоцентрической долготы выбранной одной Планеты Lo по формулам

                                                                                 Di = Li – Lo, если Li > Lo

                                                       Di = Li – Lo + 360º, если Li < Lo                                                  (1)

                                                                i = 1,2,3,4,5,6,7 – индексы (номера) планет

 

• вычисляется положительный (против часовой стрелки) угол Y1 1-го сектора планеты (см. рисунок 1) по формуле

      Y1 = min(Di)                                                         (2)

• вычисляется отрицательный угол (по часовой стрелке)  Y2 2-го сектора планеты (см. рисунок 1) по формуле

Y2 = max(Di) – 360º                                                 (3)

• вычисляется угол одиночества Земли

  Y = Y1 – Y2                                                            (4)

• вычисляется соответствующий угол сектора групп планет

S = 360º – Y                                                             (5)

Тогда положению одиночества Земли соответствуют следующие праметры

Y1 > 90º и Y2 < -90º                                                     (6)

 что, в свою очередь очередь приводит к тому, что

Y  >  180º и S < 180º                                                     (7)

Заметим, что варианты, при которых Y > 180º, но при этом Y1 < 90º или  Y2 > -90º не соответствуют определению одинокой Планеты.

Произведенные расчеты на основании ежедневных данных гелиоцентрических долгот планет показывают появления периодов одиночества Планеты, начиная с Земли, на протяжении 20-го и 21-го веков. Насколько подобные явления встречаются редко, показано в таблице 1 в течение всего 20-века и 21-века, в которой отображены экстремальные даты периодов одиночества Земли, угловые значения секторов “кучности планет”, а также длительность периодов одиночества в днях.

Таблица 1

Дата кульминации одиночества планеты	Земля Гелиоцентрическая долгота градусы	Мин-ое значение угла Y1 градусы	Макс-ое значение угла Y2 градусы	Угол Y одиночества Земли градусы	Угол S cектора планет градусы	Дата начала периода	Дата окончания периода	Длит. периода в днях
01.05.1915	220.5	93	-99.4	192.4	167.6	26.04.1915	04.05.1915	8
02.08.1942	309.7	112.1	-129.4	241.5	118.5	17.07.1942	25.08.1942	39
11.07.1944	289.2	140.8	-104.7	245.5	114.5	26.06.1944	26.07.1944	30
01.09.1947	338.3	90.5	-96.4	186.9	173.1	25.08.1947	01.09.1947	7
05.09.1953	342.6	90.6	-133.1	223.7	136.3	03.09.1953	05.09.1953	2
16.08.1955	322.8	155.9	-91	246.9	113.1	15.08.1955	08.09.1955	24
12.11.1961	49.8	97.8	-97.7	195.5	164.5	10.11.1961	19.11.1961	9
02.12.1980	70.2	106.3	-133.5	239.8	120.2	22.11.1980	19.12.1980	27
10.11.1982	47.5	158.7	-97.8	256.5	103.5	21.10.1982	28.12.1982	68
30.12.1985	98.4	90.2	-133.2	223.4	136.6	20.12.1985	30.12.1985	10
18.01.1994	117.7	94.3	-145.9	240.2	119.8	25.11.1993	22.01.1994	58
27.12.1995	94.8	172.4	-100.1	272.5	87.5	18.12.1995	31.12.1995	13
11.02.2000	141.6	105.9	-94.1	200	160	07.02.2000	11.02.2000	4
16.04.2000	206.3	98.3	-145	243.3	116.7	13.04.2000	24.04.2000	11
09.04.2002	199	109.9	-90.2	200.1	159.9	09.04.2002	25.04.2002	16
19.04.2021	208.9	97.8	-90.3	188.1	171.9	19.04.2021	27.04.2021	8
13.03.2024	172.6	128.3	-120.4	248.7	111.3	12.02.2024	19.03.2024	36
27.05.2024	245.9	95.8	-185.7	281.5	78.5	26.05.2024	02.06.2024	7
06.05.2026	225.2	136.5	-105.9	242.4	117.6	19.04.2026	02.06.2026	44
01.05.2034	220.3	134.1	-108.9	243	117	11.04.2034	09.05.2034	28
19.06.2038	267.4	101.4	-100.4	201.8	158.2	07.06.2038	22.06.2038	15
05.09.2064	342.6	104	-107.2	211.2	148.8	02.09.2064	19.09.2064	17
12.10.2075	18	90.1	-94.7	184.8	175.2	08.10.2075	12.10.2075	4
14.10.2076	20.7	92.6	-93.2	185.8	174.2	11.10.2076	16.10.2076	5
06.05.2085	225.3	96.7	-90.4	187.1	172.9	06.05.2085	12.05.2085	6
16.06.2096	264.9	100.7	-108.7	209.4	150.6	01.06.2096	27.06.2096	26

 

Из таблицы 1 видно, что общее количество периодов одиночества Земли за 2 столетия равно 26, из них 12 в 20-ом веке и 14 в 21-ом веке. Отдельно можно выделить очень длительные периоды, при которых Земля не входила в состояние одиночества, например, в 20-ом веке с 1915 по 1942 годы, а в 21-ом веке еще предстоит с 2038 по 2064 годы. Также можно отметить очень близкие следующие друг за другом события, между которыми порядка 2-х месяцев, в начале 2000-го года и в середине текущего 2024-го года. Для наглядности положений одиночества планеты Земля построим график 1, используя данные таблицы 1, на котором предельно возможные углы Y в периоды одиночества отложены по оси ординат, а даты - по оси абсцисс. Верхние экстремумы (пики) на графике, превышающие 180 градусов, полностью соответствуют признакам одиночества Планеты Земля

 

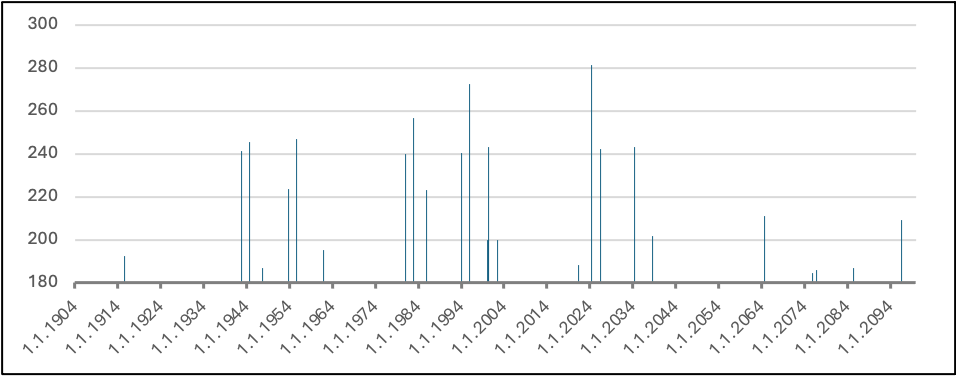
График 1. Экстремальные положения одинокой Земли на небосводе Солнца

        

Только при двух положениях одиночества планеты Земля на протяжении 2-х веков, другие планеты сгруппируются в секторе, угол которого меньше 90 градусов. Первое такое событие произошло в декабре 1995 года.   

Второе неординарное событие в Солнечной системе с точки зрения одиночества планеты Земля произойдет в своей кульминации 27 мая 2024 года, когда относительно одинокой Земли все остальные планеты сгруппируются определенным образом в небольшой и минимальный за 200 лет угол приблизительно равный 78 градусам, что показано на рисунке 3.

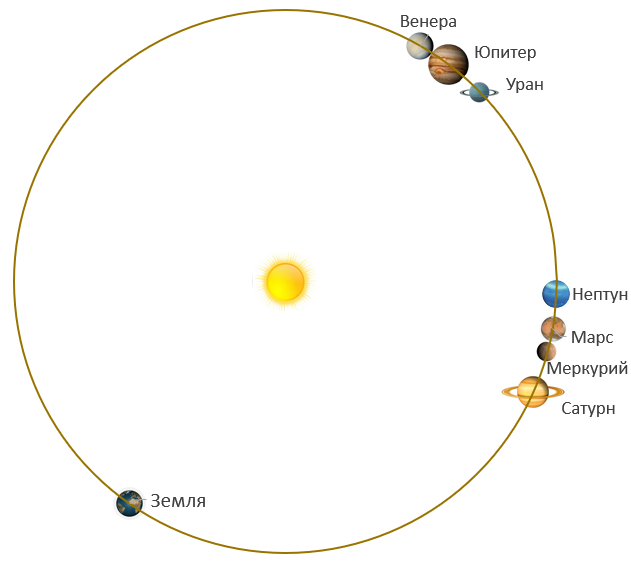
Рисунок 3. Положение Земли и планет на небосводе Солнца 27 мая 2024 года

 

Заключение. Приведенные расчеты показывают нестандартные положения Планет Солнечной Системы друг относительно друга. Существует понятие парада Планет, когда относительно Земли планеты выстраиваются в небольшом наблюдаемом с Земли угловом секторе. В данной работе практически получается “антипарад” Планет, т.к. при одиночестве Планеты Земля, ни одна из других планет практически не видна на земном небосводе в темное время суток. Заметим, что в моменты Солнечных затмений в эти периоды все планеты могли быть видны также в относительно небольшом секторе, подобно большому параду планет. Однако, проверено – ни одно событие одиночества Земли не совпадает ни с каким Солнечным затмением.

Подобные расчеты также будут выполнены в последующих Частях работы для всех Планет Солнечной Системы, что может вызывать определенный интерес, например, в небесной механике, в теории и практике гравитационных взаимодействий объектов Солнечной Системы и других научных изысканиях.