ВОЗМОЖНЫЙ ПОДХОД К ИЗУЧЕНИЮ КОСМОЛОГИЧЕСКОЙ ИНФЛЯЦИИ

Физика как наука ставит перед собой основную цель – это изучение и объяснение законов окружающей нас действительности. Для качественного достижения этой цели необходимо в освоении физических дисциплин уделять внимание на решение задач. Физическая задача – ведущий способ формирования навыков анализа физических систем и умений предсказывать (восстанавливать) их поведение во времени и пространстве.

В рамках теоретической физики это требует отдельного методического обеспечения. Решение задачи может быть рассмотрено в различных контекстах. Например, если необходимо формировать умения по составлению плана действий – необходимо проводить анализ задачи и её решение на процедурно-алгоритмическую сущность: «что и за чем последовало?», «почему именно так?», «можно ли предложить альтернативный шаг?», «как оптимизировать?» и т.д. Иначе же, анализ задачи может быть направлен на физическое понимание выполняемых шагов: «почему допустима данная процедура?», «какой физический смысл несет данная операция?», «какой вывод можно сделать из ответа задачи?» и т.д. Данные аспекты всегда присутствую в решении любой задачи в различных соотношениях. Задача может быть «тяжелой» в процедурном плане, но «легкой» в физической интерпретации, и обратно. Это первая проблема педагога – «какую именно цель он преследует в процессе обучения?»

Рассмотрим простую задачу на верификацию модели космологической инфляции:

Условие задачи:

В метрике Фридмана — Леметра — Робертсона — Уокера проверьте набор f(T) = T, H(t) = m/t  на возможность практического применения.

Решение задачи:

Шаг 1. Запишем основные уравнения космологии для телепараллельного случая (исключим вклад материи, оставив только взаимодействие модели со скалярным полем):

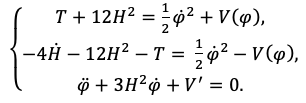                                          (1)

Шаг 2. В метрике (ФЛРУ) скаляр кручения выражается через параметр Хаббла выражением T=-6H². Также заметим, что только два уравнения независимы из трех. С учетом этого систему можно переписать в таком виде:

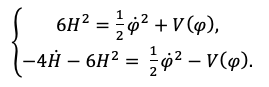                                                   (2)

Шаг 3. Обособляя V(φ) и производную φ путем суммирования и вычитания уравнений системы, получаем следующие соотношения:

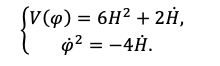                                                              (3)

Имеются два уравнения с участием переменных V, H, φ, t и производных. Для нахождения вида функций φ и V необходимо задать H(t). Так как опорная модель для параметра была взята H(t) = m/t  имеем:

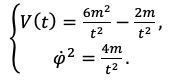                                                                         (4)

Шаг 4. Определим первые два параметра медленного скатывания путем перехода от φ к t, так как производная поля по времени может быть определена из (4) (с точностью до знака, который не влияет на значения):

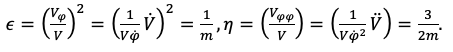                 (5)

Шаг 5. Так как оба параметра получились независимыми от времени, что упрощает анализ, необходимо с помощью них оценить согласование с наблюдательными данными, составим спектральный параметр скалярного поля и тензорно-скалярное отношение:

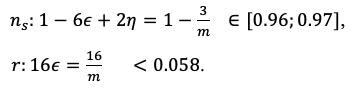                                                                       (6)         

Шаг 6. (Ответ) Как можно заметить, первое условие требует, чтобы m∈(75;100), а второе  m>275. Пересечений по m нет, а значит дальнейшее рассмотрение выбранного набора как возможную реальную модель не будет иметь смысла, так как он не прошел верификацию по наблюдаемым данным. Следует менять зависимость параметра Хаббла от времени, или вообще задавать функцию f(T) более сложного вида.

В данной задаче интересен процедурный аспект деятельности. Решение разбилось на 6 крупных шагов, каждый из которых может быть раздроблен еще на более малые шаги-операции. Запишем общий план действий, который необходимо сформировать у обучающихся при решении задач такого класса:

1. По модели f(T) составить уравнения космологии из системы [1];
2. Пренебречь вкладом материальной части (так, как на раннем этапе инфляции материя практически отсутствует), исключить скаляр T путем замены на -6H², как постоянная зависимость в плоской метрике (ФЛРУ) для телепараллельных моделей;
3. Определить функцию V(H, φ);
4. Для заданного вида H(t) определить V(φ) или V(t) исходя из полученной системы;
5. Найти параметры медленного скатывания по определению [1, 2];
6. Определить спектральные параметры и тензорно-спектральное соотношение [3];
7. Оценить полученные значения с экспериментально наблюдаемыми;
8. Сделать вывод о верифицируемости набора с моделями f(T), H(t).

Каждый шаг потребовал от учащегося иметь соответствующие процедурные навыки, которые уже должны быть сформированы на момент решения задачи. Невозможно приступить к анализу физического смысла задачи, если обучающийся не понимает алгоритмическую сторону своей деятельности. Это ставит продуктивность процесса обучения теоретической физике под сомнение.

Однако, посмотрим на представленный план операций глобально. Некоторые пункты будут повторяться в различных задачах (например пункты 1-3 – в заданиях на анализ потенциального поля какого-либо космологического объекта). Иначе говоря, педагог может использовать блочно-модульное построение курсов, посвященных космологической инфляции или дисциплинам по космологии в целом как возможная оптимизация процесса обучения [4].

Задачей педагога становится переупаковка для данной дисциплины материала, сопровождающаяся разбиением и группировкой, например, на тематические блоки формируемых умений и навыков, а далее необходимо лишь направить усилия на качественное усвоение материала в узких рамках одного блока. Хоть это и потребует затрат временный ресурсов на подготовительном этапе, но принесет положительные стороны в освоении дисциплины учащимися.

В рамках статьи было показано, что некоторые задачи по космологии могут быть разбиты на подзадачи, которые в свою очередь могут существовать как отдельные дидактические единицы. Это позволяет модернизировать процесс обучения, переведя его на блочно-модульную структуру по своему содержанию, как возможный кандидат повышения эффективности обучения.