ПРИМЕНЕНИЕ ТЕОРИИ ВЕРОЯТНОСТИ ПРИ ПЕРЕПОДГОТОВКЕ ПИЛОТОВ НА ДРУГОЙ ТИП ВОЗДУШНОГО СУДНА

Прежде чем приступать к решению задачи, давайте определим термин "теория вероятности".

Теория вероятностей — раздел математики, в котором изучаются общие закономерности случайных явлений массового характера независимо от их конкретной природы. Она разрабатывает методы количественной оценки влияния случайных факторов на различные явления. Знание этих закономерностей позволяют предвидеть, как эти события будут протекать в реальном опыте.

После ознакомления можем приступать к решению задачи. 

Прочитаем условие:

В одной из российских авиакомпаний было принято решение провести внеплановую проверку профессиональной подготовки пилотов для переобучения на новый тип воздушного судна - самолет МС21. Чтобы получить разрешение на выполнение полетов на этом самолете, пилоту требуется совершить посадку с минимальной перегрузкой в 1,2G. Существует несколько вариантов прохождения испытания. Один из вариантов включает 3 зачетные попытки, из которых пилот должен успешно совершить посадку с минимальной перегрузкой в 2 случаях, а другой – 5 зачетных попыток, из которых необходимо успешно совершить 3 посадки с минимальной перегрузкой. Пилот сам выбирает удобный для себя метод получения разрешения. Который из них будет более выгодным с точки зрения вероятности успеха для опытного командира и который для неопытного второго пилота?

Решение:

Чтобы облегчить решение, рассмотрим абстрактного пилота, а потом применим полученный результат для авиаторов из нашей задачи.

Пусть р – вероятность выполнения посадки с перегрузкой 1,2G. Тогда 1 - р – вероятность невыполнения, так как события несовместные.

В первой вариации зачета имеется 8 вариантов исхода проверки, и всего 4 из них приведут пилота к цели – получению допуска. В трех из них летчик успешно сажает самолет два раза, вероятности этих событий равны:

(1 - p) × р × р

p × (1 - p) × р

p × p × (1 - p)

Четвертый исход, включающий в себя 3 мастерских касания ВПП, произойдет с вероятностью р³.

Сложив все эти выражения, мы получим вероятность получения допуска, выбрав первый тип зачета:

((1 - p) × р × р) ×3 + р³

(p² - p³) × 3 + p³

3p² - 2p³

Теперь необходимо провести такой же анализ и для второго.

В этом случае проще применить формулу Бернулли, где р – вероятность успешной посадки, n – количество попыток, а k – количество мягких приземлений. Испытаниями Бернулли называются независимые опыты с двумя исходами (успех и неудача), причем вероятность успеха в каждом опыте одна и та же p (вероятность неудачи q  = р - 1). Формула Бернулли часто используется для расчета вероятности успеха определенного количества раз в серии испытаний.

 Нас удовлетворяют ситуации, когда пилот выполнил идеальную посадку три, четыре или пять раз.

P_n(k)=C^k_n⋅p^k⋅(1-p) ^n-k

P_n(k>=3) =C³₅⋅p³⋅(1-p)^{2 +} C⁴₅⋅p⁴⋅(1-p)¹ + C⁵₅⋅p⁵⋅(1-p)⁰ = 10 ⋅ p³⋅(1-p)² +

+ 5 ⋅ p⁴⋅(1-p)¹ + 1 ⋅ p⁵⋅(1-p)⁰ = 10 ⋅ р³ ⋅ (1-2р+р²) +5(р⁴-р⁵) +р⁵ =

= 10р³ - 20р⁴ + 10р⁵ + 5р⁴ - 5р⁵ + р⁵ = 6р⁵ - 15р⁴ + 10р³

6р⁵ - 15р⁴ + 10р³ – вероятность получения допуска при выборе второго варианта испытания.

Но какая же из полученных вероятностей выше? 3p² - 2p³ или 6р⁵ - 15р⁴ + 10р³? Мы точно можем сказать, что если вероятность выполнения равна 0, то мы не сможем получить зачет ни при каком раскладе, а если 1, то точно получим. Ну а для того, чтобы оценить свои шансы в промежуточных ситуациях воспользуемся математическим ожиданием.

Математическое ожидание – произведение результата на вероятность его получения. Примем выполнение посадки с перегрузкой 1,2G за единицу. В целом можно использовать любое значение, потому что мы используем математическое ожидание только для оценки своих шансов. В первом случае математическое ожидание равно 1(3p² - 2p³), а во втором – 1(6р⁵ - 15р⁴ + 10р³).

Чтобы понять какая вариация зачета выгоднее для пилота, изобразим два графика, показывающих зависимость математического ожидания от вероятности (график. 1).

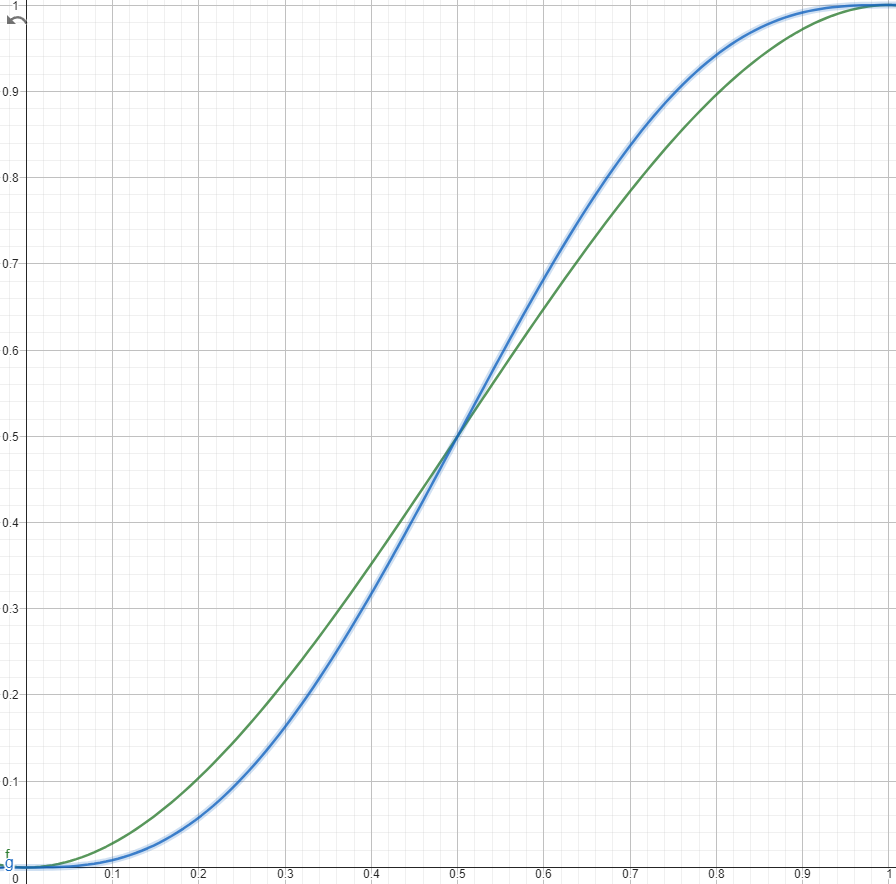
График 1. Зависимость математического ожидания от вероятности

Зеленый график соответствует первому типу зачета, а синий – второму.

Мы видим, что если вероятность выполнения пилотом мягкой посадки меньше 0,5, то лучше выбрать первый вариант аттестации, так как его математическое ожидание в этом случае выше, а если больше 0,5 – то второй. Из этого умозаключения плавно вытекает вывод.

Вывод:

Вспомним условие нашей задачи. Сдать зачет необходимо двум пилотам, один из которых является опытным командиром, а второй – неопытным вторым пилотом. Разумно предположить, что первый идеально посадит самолет с вероятностью большей, чем 0,5, а второй – меньшей. Следовательно, наибольший шанс сесть в кресло нового авиалайнера у командира наступает при выборе первого типа зачета, а у второго пилота - второго.