ВЕЙВЛЕТ АНАЛИЗ ВЛИЯНИЯ 40 ПАРАМЕТРОВ ЖИЗНИ НА МИГРАЦИЮ НАСЕЛЕНИЯ В СУБЪЕКТАХ ЗАПАДНОЙ СИБИРИ

1. Введение

Коэффициент миграционного прироста (интенсивность миграции) вычисляется как отношение миграционного прироста к среднегодовой численности постоянного населения [2].

Упрощенно понятие «миграция» расшифровывается, как смена места жительства (переезд). Явление миграции — одно из ключевых понятий демографического процесса, поскольку функционирование государства находится в прямой зависимости от данного действия. Миграция влияет на численность населения государства, определяя его экономическое положение. Понятие миграционного прироста обозначается в демографии в виде разности между теми, кто прибывает в какую-либо страну (область, территорию) на постоянное место жительства, и теми, кто ее безвозвратно покидает [3].

Этот показатель (критерий оценки) выделяется из 40 параметров жизни 14 субъектов Западной Сибири [4] для изучения влияния других факторов.

Цель исследования –выявление устойчивых волновых закономерностей [5-7] изменения параметра Х29 – коэффициента миграционного прироста на 10⁴ населения на территории 14 субъектов федерации Западной Сибири.  

 

2. Материалы и методы

Составлены данные относительно геодезических координат центров столиц субъектов федерации Западной Сибири: видов угодий, экологических, демографических и социально-экономических показателей. 

В таблице 1 приведен фрагмент исходных данных по 14 субъектам из сайта https://rosstat.gov.ru/accounts, в частности из (Российский статистический ежегодник, 2019). Данные по координатам и климату взяты из (Координаты в городах России, n.d.) и (Среднемесячные климатические данные, n.d.).

Удельные и относительные параметры распределяются по группам:

I) координаты центров столиц субъектов федерации (Х01 – приведенная северная широта, причем , ⁰; Х02 – приведенная восточная долгота, причем , ⁰; Х03 – высота над уровнем Балтийского моря, м);

II) климатические среднемесячные параметры за 30-летний период 1961-1990 гг. (Х04 – средняя ночная температура, ⁰С; Х05 – средняя дневная температура, ⁰С; Х06 – средняя сумма осадков, мм; Х07 – среднее число дней с осадками >0,1 мм, шт.); 

III) параметры погоды за 2018 год (Х08 – средняя температура в январе, ⁰С; Х09 – средняя температура в июле, ⁰С; Х10 – сумма осадков за январь, мм; Х11 – сумма осадков за июль, мм);

Таблица 1 – Фрагмент исходных данных по 40 параметрам

Код	Субъект федерации	Столица	Х01	Х02	…	Х29	…	Х40
45	Курганская область	Курган	5.45	5.3333	…	-77.2	…	262.2
66	Свердловская область	Екатеринбург	6.8519	0.6122	…	-3.0	…	251.9
72	Тюменская область	Тюмень	7.1522	5.5272	…	28.4	…	174.1
74	Челябинская область	Челябинск	5.154	1.4291	…	-25.7	…	251.0
4	Республика Алтай	Горно-Алтайск	1.9606	25.9189	…	-15.7	…	222.3
17	Республика Тыва	Кызыл	1.7147	34.4534	…	-30.3	…	378.1
19	Республика Хакасия	Абакан	3.7156	31.4292	…	-16.7	…	249.9
22	Алтайский край	Барнаул	3.3606	23.7636	…	-31.7	…	260.1
24	Красноярский край	Красноярск	6.0184	32.8672	…	-1.0	…	262.1
38	Иркутская область	Иркутск	2.2978	44.296	…	-24.6	…	320.1
42	Кемеровская обл. - Кузбасс	Кемерово	5.3333	26.0833	…	-31.3	…	342.8
54	Новосибирская область	Новосибирск	5.0415	22.9346	…	28.8	…	232.1
55	Омская область	Омск	4.9924	13.3686	…	-62.0	…	220.3
70	Томская область	Томск	6.4977	24.9744	…	-6.2	…	201.3

Примечание: Выделены субъекты федерации Ангаро-Енисейского макрорегиона.

 

IV) доли (%) угодий и их комплексов к площади суши (Х12 – сельхозугодий; Х13 – лесов; Х14 – пашни; Х15 – растительного покрова «трава + кусты + деревья»; Х16 – измененные человеком угодья; Х17 – общий экологический коэффициент, рассчитываемый как отношение площади растительного покрова к площади измененных человеком угодий);

V) удельные потребление воды, сброс и выброс загрязнений (Х18 – забор воды, м³/чел.; Х19 – использование воды, м³/чел.; Х20 – сброс загрязнений, м³/чел.; Х21 – выбросы в атмосферу загрязняющих веществ, кг/чел.; Х22 – улавливание загрязняющих веществ из выбросов, кг/чел.); 

VI) параметры населения (Х23 – плотность, чел./км²; ожидаемая продолжительность жизни, лет: Х24 – всех; Х25 – мужчин; Х26 – женщин);

VII)   демографические параметры населения (Х27 – суммарный коэффициент рождаемости; Х28 – младенческая смертность на 1000 родившихся живыми; Х29 – коэффициент миграционного прироста на 10⁴ населения; Х30 – естественный прирост на 1000 населения);

VIII) параметры хозяйства (Х31 – уровень занятости, %; Х32 – уровень безработицы, %; Х33 – доля населения ниже прожиточного минимума, %; Х34 – доля городского населения, %; Х35 – доля сельского населения, %)

IX) экономические параметры производства (Х36 – валовый региональный продукт (ВРП) на душу населения за 2018 год, тыс. руб./чел.; Х37 – средние душевые доходы населения, руб./ мес.; число умерших в трудоспособном возрасте на 10⁵ населения, чел.: Х38 – оба пола населения; Х39 – мужчины в возрасте 16-59 лет; Х40 – женщины в возрасте 16-54 года).

Колебания (вейвлет сигналы) записываются формулой [4-7] вида

, , ,  (1) 

где  – показатель,  – номер составляющей (1),  – объясняющая переменная,  – параметры (1), идентифицируемые в CurveExpert-1.40 (URL: http://www.curveexpert.net/);  – амплитуда (половина),  – полупериод. 

 

3. Иерархия трехчленных моделей

Коэффициенты корреляции после идентификации формулы (1) по мере снижения адекватности трехчленных моделей приведены в таблице 2.  

Таблица 2 – Иерархия моделей влияния на Х29 с двухчленным трендом и вейвлетом

Х29	0.9488	0.9906	Х07	0.2963	0.8856	Х08	0.2927	0.6743
Х02	0.3893	0.9547	Х38	0.5729	0.8828	Х31	0.5728	0.8198
Х13	0.4136	0.9537	Х28	0.6535	0.8819	Х40	0.4763	0.8095
Х16	0.7786	0.9509	Х23	0.7654	0.8800	Х34	0.3549	0.8018
Х12	0.5178	0.9221	Х24	0.3733	0.8785	Х33	0.3650	0.8000
Х14	0.6204	0.9129	Х37	0.6404	0.8699	Х01	0.5570	0.7838
Х21	0.4012	0.9015	Х36	0.6461	0.8586	Х26	0.3068	0.7222
Х09	0.5639	0.8973	Х19	0.4673	0.8521	Х15	0.4448	0.7037
Х03	0.4354	0.8949	Х06	0.4811	0.8492
Х18	0.5253	0.8890	Х30	0.6868	0.8454	Х25	0.5049	0.6869
Х17	0.6167	0.8858	Х39	0.5913	0.8428	Х22	0.3673	0.5982

 

В таблице 2 приняты условные обозначения:  – влияющая переменная;  – формула тренда;  – формула трехчленного вейвлета.

Ранговое распределение Х29 получает наибольшее значение коэффициента корреляции 0.9906, по тренду оно равно 0.9488. Из 40 факторов дополнительный к тренду вейвлет дал сильные связи (коэффициент корреляции не менее 0.7) для 30 параметров (75%). Два (Х25 и Х22) дали адекватность ниже 0.7. Остальные восемь параметров не позволили идентифицировать (1) и дали рейтинг по трендам: Х32 0.5861; Х10 0.4141; Х04 0.2504; Х11 0.2268; Х05 0.1427; Х27 0.1226; Х35 0.1122; Х20 0.1032.

  

4. Ранговое распределение миграционного прироста

Идентификацией (1) получены параметры в таблице 3 (рис. 1, рис. 2).

Таблица 3 – Параметры модели (1) влияния рангов на миграционный прирост

Номер	Асимметричный вейвлет								Коэф. корр.
	Амплитуда (половина) колебания				Полупериод колебания			Сдвиг
1	32.27054	0	0.40831	1	0	0	0	0	0.9906
2	-3.76616	0.96854	0	0	0	0	0	0
3	0.038638	0	-0.033065	2.13422	10.53660	-0.066294	1.76684	-1.34374
4	14.40353	0	0.20747	1.29490	1.49949	-0.0075736	1.75619	-4.47848	0.9854
5	4.56688	3.28331	2.16041	0.70695	9.45635	-0.89900	1.00230	-2.03586	0.9477
6	-0.0035616	2.91456	0.00048126	3.79405	0.012331	0.014922	1.04165	-2.77808	0.9520
7	-0.23169	0	0.47923	1	1.54291	0.029611	1.32387	0.92441	0.7914
8	3.28814e-11	17.34714	1.80268	1.00336	0.55058	0.028379	1.00495	3.39159	0.9779`

 

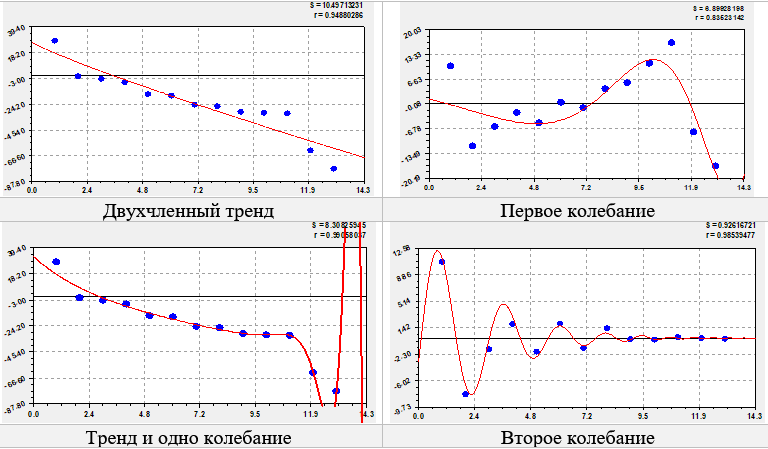
Рис. 1. Фрактальное распределение коэффициента миграционного прироста
(в правом верхнем углу:  S  – стандартное отклонение; r   – коэффициент корреляции)

 

Из восьми членов первые два образуют тренд, у которых период колебания стремится к бесконечности. Первый член является законом Мандельброта (в физике), Лапласа (в математике), Перла-Ципфа (в биологии) и Парето (в эконометрике). Второй кризисный член является степенной функцией. По возможностям CurveExpert-1.40 три члена дают общий коэффициент корреляции 0.9906. Остальные пять вейвлетов имею сильную адекватность выше 0.7.  

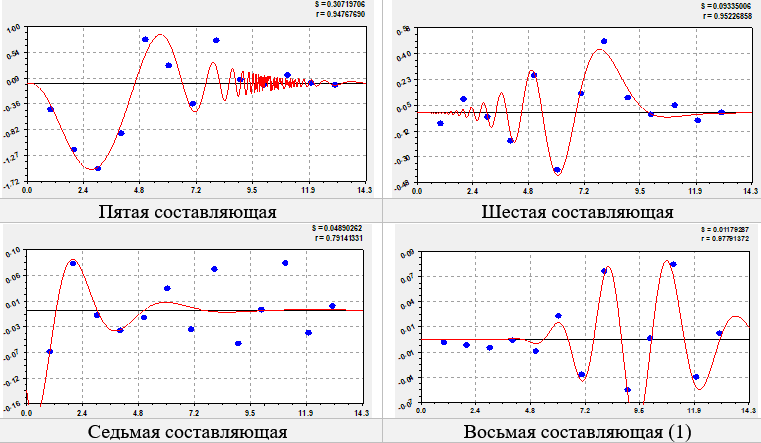
Рис. 2. Фракталы коэффициента миграционного прироста по последним членам

Этот показатель имеет ранг от нуля по вектору предпорядка предпочтительности «лучше-хуже» (табл. 4) от положительных значений (приток мигрантов) до наибольших отрицательных значений (отток населения).

Таблица 4 – Относительные погрешности расчетных от фактических значений

Ранг R	Критерий Х29	4 члена		6 членов		8 членов
		остатки	погрешн	остатки	погрешн	остатки	погрешн
13	-77.2	-0.0313846	0.04	0.00703393	-0.01	0.00786617	-0.01
3	-3.0	-1.49764	49.92	-0.00929439	0.31	-0.00883962	0.29
1	28.4	-0.461859	-1.63	-0.0717416	-0.25	-0.00328358	-0.01
8	-25.7	0.75079	-2.92	0.0710225	-0.28	0.00177187	-0.01
5	-15.7	0.769588	-4.90	-0.013355	0.09	-0.0084678	0.05
9	-30.3	0.0651602	-0.22	-0.0579334	0.19	0.00379448	-0.01
6	-16.7	0.31134	-1.86	0.0378248	-0.23	0.00712175	-0.04
11	-31.7	0.144927	-0.46	0.0816219	-0.26	0.0146958	-0.05
2	-1.0	-1.16106	116.11	0.08095	-8.10	-0.00645677	0.65
7	-24.6	-0.356125	1.45	-0.0337588	0.14	0.00736312	-0.03
10	-31.3	-0.0273671	0.09	0.000307547	0.00	0.00958697	-0.03
0	28.8	-0.140704	-0.49	-0.140704	-0.49	-0.0011581	0.00
12	-62.0	0.0085593	-0.01	-0.0399636	0.06	0.0116179	-0.02
4	-6.2	-0.879555	14.19	-0.0352646	0.57	-0.0018906	0.03

После восьмого члена максимальная относительная погрешность равна всего 0.29%. Тогда 14 субъектов федерации имеют между собой сильнейшую функциональную связность по коэффициенту миграционного прироста.    

 

5. Фрактальное распределение вейвлетов

Восемь вейвлетов из таблицы 3 распределяются как некратные фракталы, в первом члене по модифицированному нами закону Мандельброта (табл. 5 и рис. 3), для стандартного (среднеквадратичного) отклонения так:

                                      

                        

    .                          (2)

Таблица 5 – Погрешности расчетных значений стандартного отклонения

Ранг	Коэф. корр.	Станд. откл.	Расчетное стандарт. отклонение
				Остаток	Погр. ,%
0	0	29.147	29.147	-1.42E-06	0.00
2	0.9488	10.497	10.500	-0.00278474	-0.03
3	0.9906	8.308	8.305	0.00253895	0.03
4	0.9454	0.926	0.930	-0.00353537	-0.38
5	0.9477	0.307	0.300	0.00666428	2.17
6	0.9520	0.093	0.092	0.00109193	1.17
7	0.7914	0.049	0.047	0.00185499	3.79
8	0.9779	0.012	0.012	0.00021379	1.78

 

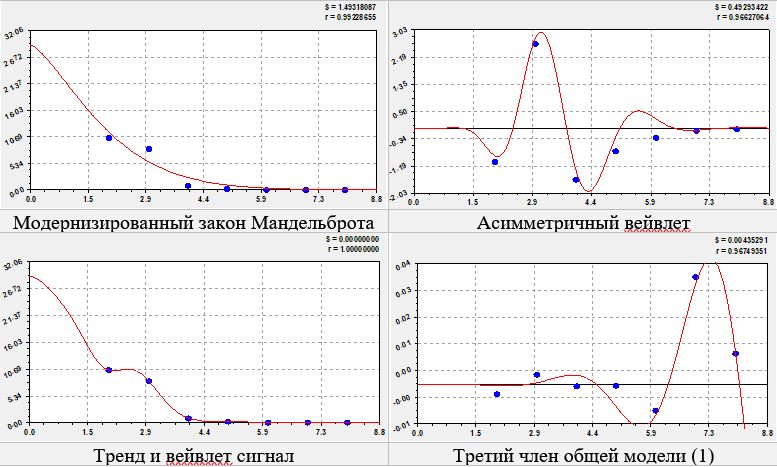
Рис. 3. Ранговые распределения стандартного отклонения у вейвлетов по таблице 3

Тогда получается, что коэффициент миграционного прироста не только показывает тесную функциональную связь между 14 субъектами федерации Западной Сибири, но сами эти колебательные связи в виде вейвлетов появляются с высокой точностью по фрактальному распределению.

6. Сверхсильные влияния на миграционный прирост

Для сопоставления парных отношений по возможностям CurveExpert-1.40 из таблицы 2 приняты по три составляющие модели (1). Из данных таблицы 2 также видно, что эти пары влияния на миграционный прирост имеют коэффициент корреляции не менее 0.95 (сверхсильные факторные связи).

Рассмотрим каждую пару влияния Х02 Х29, Х13 Х29 и Х16 Х29. 

Влияние восточной долготы на миграцию. На рисунке 4 показаны графики влияния этого параметра на показатель Х29, а в таблице 6 приведены значения параметров модели (1) как обобщенного асимметричного вейвлета.

Рис. 4. Графики вейвлет анализа влияния восточной долготы Х02 на миграцию

Тренд содержит два члена. Первый является постоянным членом в -20.43204 чел. и это характеризует среднестатистическую интенсивность миграции для всех 14 субъектов Западной Сибири.

Таблица 6 – Параметры модели (1) коэффициента миграционного прироста

Номер	Асимметричный вейвлет								Коэф. корр.
	Амплитуда (половина) колебания				Полупериод колебания			Сдвиг
Влияние восточной долготы Х02
1	-20.43204	0	0	0	0	0	0	0	0.9547
2	3.99273e-90	112.6927	6.23037	1	0	0	0	0
3	-26.44866	0.48866	0.00046039	2.89504	0.19376	0	0	0
4	0.00087891	0	-0.30856	1	3.46132	-0.0012472	1	-1.54955	0.7869
5	-7.04797	0.58517	0.085347	1	1.13328	0	0	3.67998	0.8129
6	-3.48193e-8	10.08608	0.54434	1	5.96043	-0.11290	1	-2.55443	0.8705
Влияние доли лесов от суши Х13
1	-4.95454e6	0	1.90040	0.33948	0	0	0	0	0.9537
2	6.70098e6	0.28237	2.47513	0.31777	0	0	0	0
3	36103.5523	0	2.13250	0.31097	1.16798	0.011939	1.17171	2.41956
Влияние дли измененных человеком доли угодий Х16
1	-132.66157	0	0.65509	1	0	0	0	0	0.9509
2	-1.5888e-92	85.16261	2.47917	1	0	0	0	0
3	34.30428	0	0.011121	1	3.52515	0.065791	0.36729	1.01108
Влияние доли сельхозугодий от суши Х12
1	-8.89859	0	-0.0023927	0.96163	0	0	0	0	0.9221
2	-2.3424e-24	13.98952	0	0	0	0	0	0
3	0.049439	2.56804	0.14096	0.76716	-0.61101	1.56196	0.057060	3.42768
Влияние доли пашни от суши Х14
1	-19.76624	0	0.13801	1	0	0	0	0	0.9129
2	-3.88646e-8	7.28526	0.013846	1.65775	0	0	0	0
3	-1.57084e9	22.95622	35.93055	0.28978	0.19954	0.13496	0.85618	-2.15363
Влияние выбросов загрязняющих веществ в атмосферу Х21
1	-36.31046	0	0.00081760	1	0	0	0	0	0.9015
2	1.42388	0.47954	0	0	0	0	0	0
3	-4.52701e-9	11.68534	2.03327	0.58917	1.23731	0	0	0.097974

 

Второй член является биотехническим законом [4-7] и показывает влияние Западно-Сибирской низменности по восточной долготе. Третий член является вейвлетом с постоянным периодом колебания в 0.19376 градус. Четвертый член с переменным (уменьшающимся) периодом колебания содержит нарастающую амплитуду (половину) по закону Мандельброта (в физике). При этом члены №2 и №4 имеют направленность на снижение коэффициента миграционного прироста (положительный знак), а остальные с отрицательным знаком ориентированы на увеличение показателя оттока населения.    

Из-за малого объема статьи по влиянию остальных переменных в таблице 6 и далее показаны только по три члена модели (1).

Влияние доли лесов на миграцию. Это влияние (рис. 5) заняло второе место по данным таблицы 2 (не считая рангового распределения Х29).

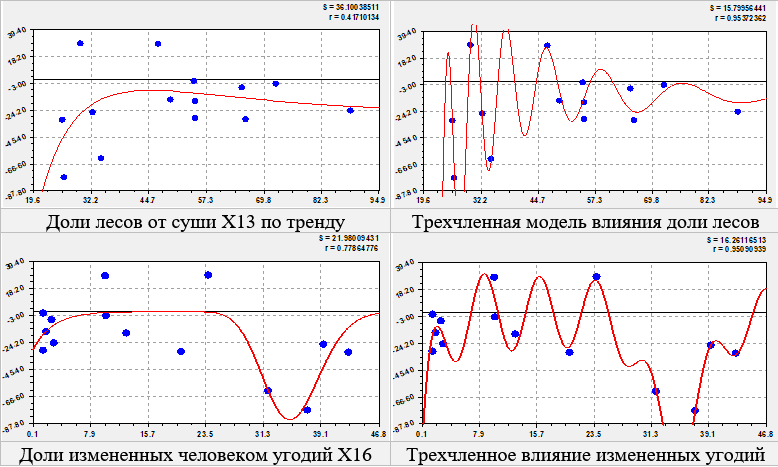
Рис. 5. Графики вейвлет анализа влияния на коэффициент миграционного прироста

Без доли лесов (при нуле) миграция составила бы -495454 чел., минимум по тренду оттока населения наблюдается при лесистости (относительно суши) 45%. Рациональная доля лесов находится в интервале 38-57%. При меньшей доле лесов от суши отток населения резко нарастает, а при превышении рационального интервала также медленно увеличивается как отток населения. Колебание миграции нарастает по мере снижения лесистости.    

Влияние измененных угодий на миграцию. С точки зрения экологии любые изменения земель (пашни, застройки, дороги, нарушенные земли, прочие земли) недопустимы. Однако из графика тренда на рисунке 5 видно, что рациональной является интервал доли измененных угодий 8-24% от суши. В этом интервале коэффициент миграционного прироста равен нулю 

При меньших значениях влияющей переменной наблюдается очень низкая освоенность территории и этот фактор увеличивает отток населения. Сильнейший отток населения наблюдается при доле измененных угодий в 35%. Энергетическая яма наблюдается от 24 до 50% измененной территории, но почему при выше 50% наблюдается нулевой коэффициент миграционного прироста?  Для ответа на этот вопрос нужны дополнительные исследования.    

7. Сильнейшие парные отношения

Такой уровень адекватности (от 0.9 до 0.95) имеется у трех пар факторов Х12 Х29, Х14 Х29 и Х21 Х29 (табл. 6 и рис. 6).    

Влияние доли сельхозугодий на миграцию. До 40% доли сельхозугодий отток населения медленный, а после 40% этот процесс ускоряется. Этому ускорению способствует второй член модели по степенной функции. Колебание нарастает по амплитуде до 55%, а затем уменьшается. Но это колебание положительное, поэтому его нужно подвергнуть амплитудно-частотному анализу, так как оно направлено на снижение оттока населения.    

Влияние пашни на миграцию. Рациональный интервал доли пашни от суши находится в интервале 7-12%, при котором наблюдается нулевой миграционный прирост. После этого интервала наблюдается энергетическая яма.  

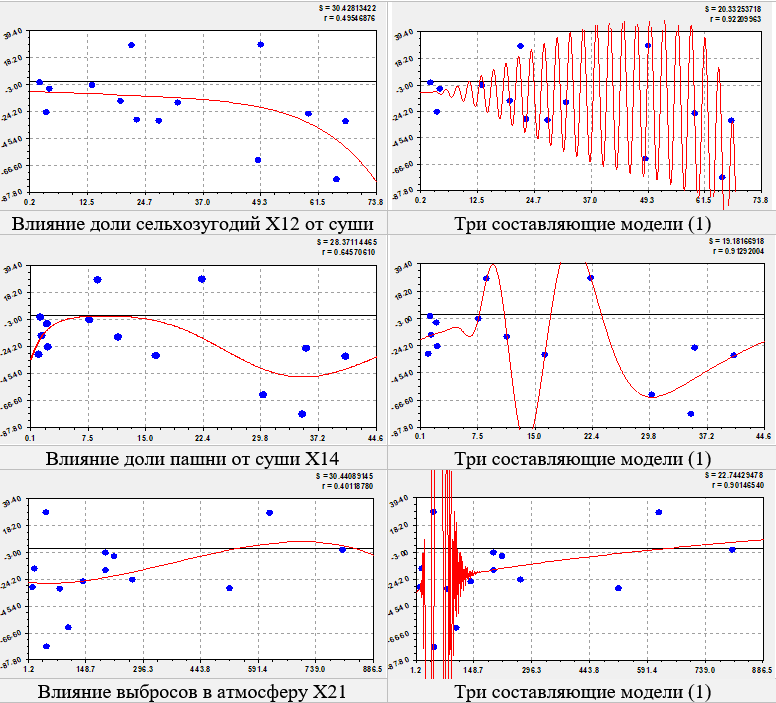
Рис. 6. Графики вейвлет анализа влияния на коэффициент миграционного прироста

Колебание начинается с полупериода 0.19954 чел. при нулевой доле пашни, а затем возрастает по закону степенной функции.    

Влияние выбросов в атмосферу на миграцию. По тренду на рисунке 6 с увеличением выбросов загрязняющих веществ по первому члену (закон Мандельброта экспоненциального убывания) происходит снижение оттока населения. Здесь срабатывает природное чутье людей – не жить на территории с загазованным воздухом. Однако по второму положительному члену происходит увеличение притока населения по степенной функции. Ясно, что это стремление за заработком. В итоге при выбросах в атмосферу 740 кг/чел. наблюдается максимальный приток населения в 4-5 человек на 10⁴ населения. При этом волна возмущения наблюдается только в начале до 150 кг/чел.    

 

8. Сильные парные отношения

Рассмотрим значимые пары факторных отношений из таблицы 2 влияния на коэффициент миграционного прироста Х29: влияние Х09, затем Х03, Х18, Х17, Х07, Х38, Х28, Х23, Х24, Х37, а также Х36, Х19, Х06, Х30, Х39, Х08, Х31, Х40, Х34, Х33, Х01, Х26 и Х15.

Влияние средней температуры в июле. На верхней границе сильных формул с коэффициентом корреляции 0.8973 на коэффициент миграционного прироста оказывает влияние Х09 средняя температура в июле 2018 г. (рис. 7).

Параметры трехчленных моделей приведены в таблице 7.

Интересно отметить, что от 10.8 до 18.5 ⁰С по тренду коэффициент миграционного прироста остается постоянным. Но после 18.5 ⁰С происходит резкое увеличение оттока населения. При этом положительное влияние на приток населения колебательной адаптацией происходит по амплитуде, возрастающей по степенной функции. Полупериод колебания с повышением температуры в июле возрастает, то есть происходит успокоение населения. 

Влияние высоты над уровнем Балтийского моря. По тренду рациональные значения высоты наблюдаются в интервале 130-180 м при минимуме оттока населения. Со снижением высоты отток населения резко возрастает, а при превышении рациональных значений также отток медленно возрастает. Колебание происходит только на высоте меньше 130 м.   

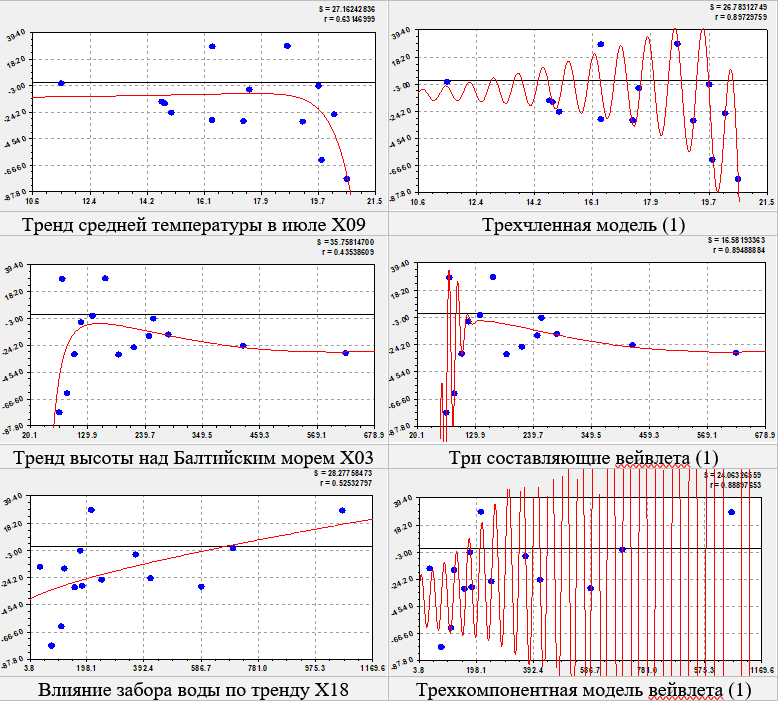
Рис. 7. Графики вейвлет анализа влияния на коэффициент миграционного прироста

Такое изменение оттока населения связано, по-видимому, с повышенной вероятностью затопления на высоте менее 130 м.

Влияние забора воды. Оказалось, что рост забора воды на территории значительно влияет на прирост населения (рис. 7 и табл. 7). Если при заборе воды всего 3.8 м³/чел. по тренду значение коэффициента миграционного прироста равно -40 чел. А при заборе воды 1170 м³/чел. миграция получает положительное значение +18 чел. При этом колебание возрастет по амплитуде от 2 х 18.44 = 36.88 м³/чел. в начале колебательной адаптации. На переход от оттока к притоку населения сказался второй член в виде степенной функции.

 

Таблица 7 – Параметры модели (1) коэффициента миграционного прироста

Номер	Асимметричный вейвлет								Коэф. корр.
	Амплитуда (половина) колебания				Полупериод колебания			Сдвиг
Влияние средней температуры в июле Х09
1	-18.39108	0	0.00037849	3.02081	0	0	0	0	0.8973
2	-1.05098e-44	34.93132	0	0	0	0	0	0
3	0.00020058	4.21211	0	0	0.28799	0.0020627	1.15103	4.83931
Влияние высоты центра столицы субъекта федерации над уровнем Балтийского моря Х03
1	-1.68627e10	0	6.58077	0.25292	0	0	0	0	0.8949
2	-8.94896e-9	5.28118	0.68950	0.94473	0	0	0	0
3	-2.75948e-43	30.73586	0.48991	0.95644	3.26792	0.024288	0.98313	-3.97176
Влияние забора воды Х18
1	-39.78412	0	-0.0024696	1	0	0	0	0	0.8890
2	0.016307	1.46357	0	0	0	0	0	0
3	-19.23527	0	-0.0040231	1	18.44330	0.055419	0.68154	4.52682
Влияние общего экологического коэффициента Х17
1	-0.031403	0	-6.26644	0.076355	0	0	0	0	0.8858
2	1.17995e6	5.09199	15.29383	0.16359	0	0	0	0
3	46.74997	0	0.020681	1	1.48894	0	0	0.74816
Влияние среднего числа дней с осадками более 0.1 мм Х07
1	-2.9706e-26	0	-59.99996	0.0089393	0	0	0	0	0.8856
2	6.18911e7	60.37945	116.17304	0.20049	0	0	0	0
3	7.0227e-103	75.80441	1.14376	1	2.38980	0	0	4.08374
Влияние числа умерших обоего пола в трудоспособном возрасте Х38
1	1720.0915	0	-0.0014778	1	0	0	0	0	0.8811
2	-13.49932	0.89813	0	0	0	0	0	0
3	2.8986e-128	58.24727	0.14779	1	6.08432	0	0	-4.48734

 

Тогда получается, что хозяйствующим субъектам необходимо, прежде всего, для привлечения людей со стороны обращать внимание на рост забора воды и предупреждение наводнений и затоплений территории.

Влияние общего экологического коэффициента. Общий экологический коэффициент вычисляется делением доли растительности в целом и по классам почвенного покрова (по классификации ООН) на общую долю антропогенных (измененных человеком) угодий [5].

В итоге он становится интегральным критерием качества растительного покрова на данной территории (табл. 7 и рис. 8).

Из графика тренда видно, что рациональный интервал этого критерия находится от 6 до 22. Здесь происходит приток населения. При этом колебание происходит с постоянным полупериодом 1.5 с уменьшающейся по закону Мандельброта амплитудой. Тогда общий экологический коэффициент становится хорошим показателем для оценки процесса миграции.  

Влияние среднего числа дней с осадками более 0.1 мм (1961-1990).  

Осадки за 30 лет оказывают сложное действие на процессы миграции людей. По тренду из таблицы 7 в начале повышения числа дней осадков от 33.4 до 65 дней происходит повышение оттока населения, затем в интервале от 65 до 116 суток характерен рост притока, а после 116 суток наблюдается резкий отток населения. Колебательная адаптация происходит от 40 до 95 суток с осадками.    

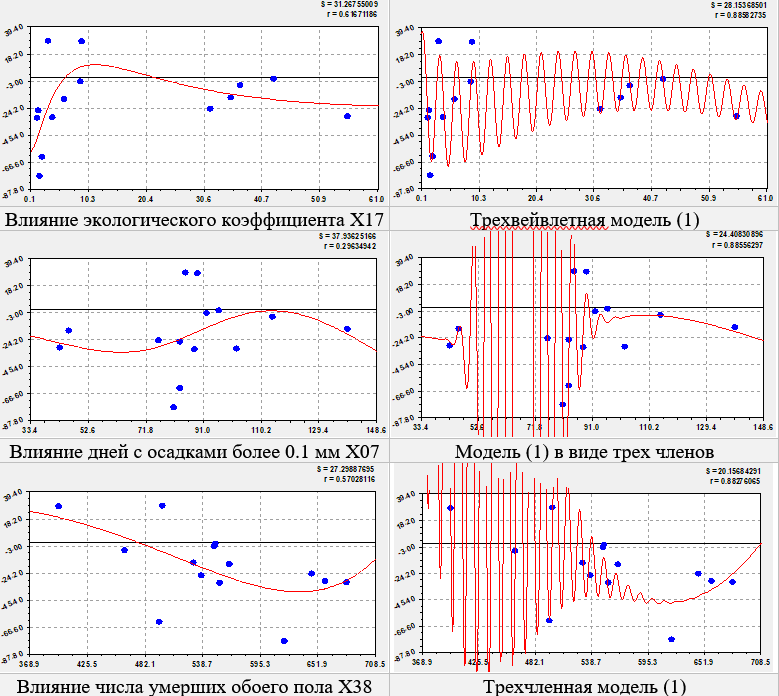
Рис. 8. Графики вейвлет анализа влияния на коэффициент миграционного прироста

По остаткам дальше возможен вейвлет анализ. Как правило, на останов влияет пара противоположно относительно оси абсцисс расположения точек.

Влияние числа умерших в трудоспособном возрасте (оба пола). По тренду (рис. 8) с увеличением числа умерших работников от 309 до 710 человек происходит переход от притока в 20 человек к максимальному оттоку в -40 человек при числе умерших в 640 человек, а затем отток даже понижается. Колебание происходит при постоянном полупериоде 6.08 человек смертей.

Последующие пары факторов приведены в таблице 8 (рис. 8 и рис. 10).

Таблица 8 – Параметры модели (1) коэффициента миграционного прироста

Номер	Асимметричный вейвлет								Коэф. корр.
	Амплитуда (половина) колебания				Полупериод колебания			Сдвиг
Влияние младенческой смертности на 1000 родившихся живыми Х28
1	42.33660	0	0.12295	1	0	0	0	0	0.8811
2	-0.51268	2.81853	0.098751	1	0	0	0	0
3	0.013322	0	-1.86255	0.77381	0.22852	0.0012756	1.01632	4.61081
Влияние  плотности населения субъектов Западной Сибири Х23
1	-7.91578	0	0	0	0	0	0	0	0.8800
2	-2.92573e-91	138.4279	10.92469	1	0	0	0	0
3	8.77157e-8	0	0.53449	1.036648	13.19226	09,15879	0.62299	-1.76411
Влияние  ожидаемой продолжительности жизни всех Х24
1	-1034.9315	0	0	0	0	0	0	0	0.8785
2	14.39614	1	0	0	0	0	0	0
3	-4.93052e5	0	0.13026	1	0.14116	0	0	-1.31014
Влияние  средних душевых доходов населения за 2018 год Х37
1	-111.51146	0	0	0	0	0	0	0	0.8699
2	0.0011341	1.10473	0	0	0	0	0	0
3	20.59576	0	-6.15893e-5	0.81156	933.78327	0.00032735	1.05569	-4.51499
4	-9.08958e-8	2.20407	0.00016663	0.97928	946.87063	0.0050029	1.00059	-4.48356	0.7180
5	-4.75568e-14	3.24743	0	0	10002.683	0	0	1.13292	0.7231
6	-5.58515e-7	2.07733	0.00025865	0.97884	510.95341	-0.00082046	1.03309	-0.36442	0.5459
Влияние  валового регионального продукта на душу населения за 2018 год Х36
1	-76.85021	0	-0.00054267	1	0	0	0	0	0.8586
2	0.64462	0.79328	0	0	0	0	0	0
3	-3.88477e-8	4.21579	0.011360	1	2.47306	0	0	2.16562
Влияние  использования воды Х19
1	-37.39453	0	0	0	0	0	0	0	0.8521
2	0.016079	1	0	0	0	0	0	0
3	-42.41826	-0.016212	0.00017234	1	80.95791	0.20958	0.73658	5.78285

 

Влияние среднедушевых доходов приведено с шестью вейвлетами.    

Влияние младенческой смертности. Эвристически понятно, что людей не привлекают территории с высокой младенческой смертностью, то есть там, где плохо развито –медицинское обеспечение рожениц (табл. 8 и рис.9).  

Первый член тренда является законом Мандельброта, а второй кризисный член – биотехническим законом. Поэтому при младенческой смертности от 3.2 до 7.7 на 1000 родившихся живыми происходит значительное снижение коэффициента миграционного прирост от +28 до -42 человек на 10⁴ населения. Но, после младенческой смертности 7.7 происходит приток населения (?).

Влияние плотности населения. При любой плотности населения (чел./км²) наблюдается постоянный отток населения в -7.9 человек.

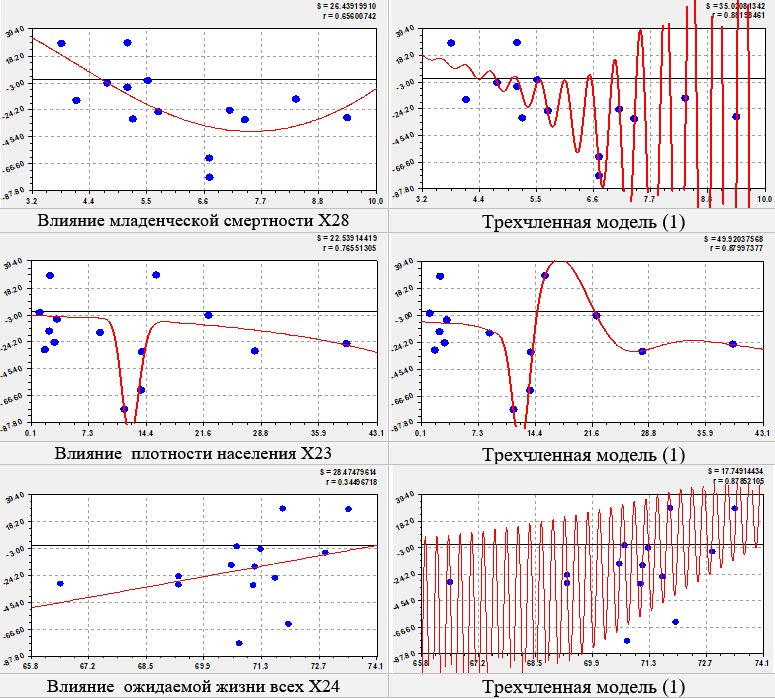
Рис. 9. Графики вейвлет анализа влияния на коэффициент миграционного прироста

Затем по кризисному биотехническому закону образуется мощная энергетическая яма с 7.3 до 17 чел./км², в которой отток населения может достичь до -100 чел. на 10⁴ населения. Однако колебание дает в интервале плотности населения от 17 до 22 чел./км² резкий всплеск притока населения. Тогда плотность населения становится высоко динамичной влияющей переменной. 

Влияние ожидаемой продолжительности жизни (всех). Тренд изменяется по линейной модели (табл. 8 и рис. 9). Теоретически при «нулевой» продолжительности жизни отток населения равен -1034.9 человек, то в этом случае каждый десятый человек уезжает из такой местности.

Рост притока населения происходит по линейной формуле 14.39614Х24, на увеличение ожидаемой продолжительности жизни на год в Западную Сибирь прибывает 14.4 чел. на 10⁴ населения. Поэтому увеличение качества жизни населения (базиса, без учета надстройки общества) – главная задача. 

Влияние средних душевых доходов. Из данных (табл. 8) видно, что всего идентифицировано пять вейвлетов.

На рисунке 10 показаны тренд и совместная трехчленная модель.

При условии Х37 = 0 образуется постоянный член в -111.5 человек на 10⁴ населения. С ростом среднедушевых доходов происходит приток населения по степенной функции.

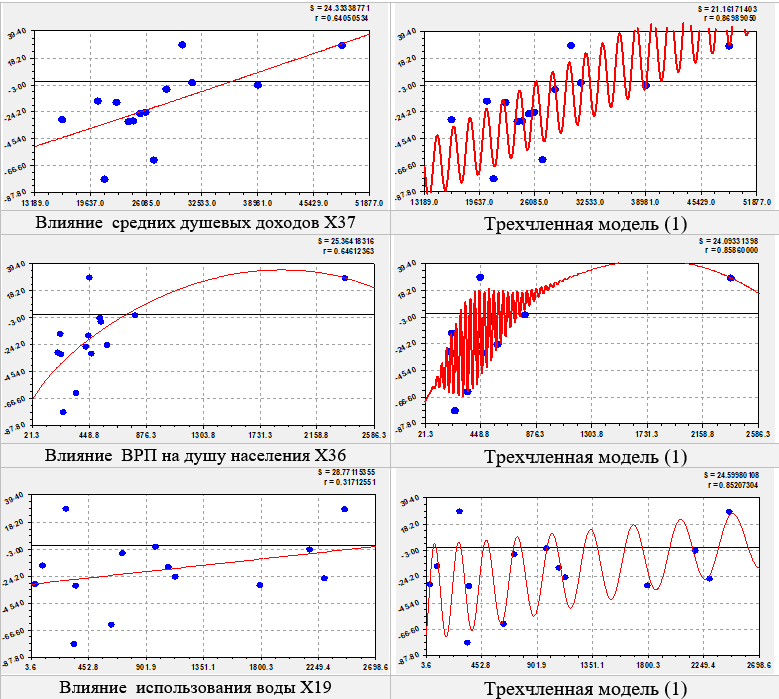
Рис. 10. Графики вейвлет анализа влияния на коэффициент миграционного прироста

Третий член в виде вейвлета позволяет медленно расти коэффициенту миграционного прироста по модифицированному нами закону Мандельброта. При этом, с увеличением среднедушевых доходов, полупериод колебания также возрастает (частота снижается), то есть люди, хотя и больше волнуются в сравнении с бедными, но по колебательной адаптации успокаиваются. Остальные три колебания являются кризисными из-за отрицательного знака, поэтому они требуют дополнительного амплитудно-частотного анализа.   

Влияние ВРП на душу населения. До 770 тыс. руб./чел. происходит по тренду достижение нулевой миграции. Далее от 770 до 1950 тыс. руб./чел. возрастает приток населения от нуля до +35 человек на 10⁴ населения. В основном колебательная адаптация наблюдается при отрицательных значениях коэффициента миграционного прироста.

Влияние использования воды. По формулам из таблицы 8 получается, что без использования воды отток населения постоянно равен -37.4 человека на 10⁴ населения. График тренда (рис. 10) показывает линейный рост коэффициента миграционного прироста до 0 при использования воды в 2600 м³/чел.

Так можно продолжать подробный анализ влияния всех 40 влияющих переменных на коэффициент миграционного прироста.

 

9. Заключение

Выявлены устойчивые волновые закономерности изменения показателя Х29 – коэффициента миграционного прироста на 10⁴ населения на территории 14 субъектов федерации Западной Сибири от влияния других 39 переменных.  

Ранговое распределение Х29 получает наибольшее значение коэффициента корреляции 0.9906. Из 40 факторов дополнительный к тренду вейвлет дал сильные связи (коэффициент корреляции не менее 0.7) для 30 параметров (75%). Два (Х25 и Х22) дали адекватность ниже 0.7. Остальные восемь параметров не позволили идентифицировать вейвлет сигнал. Из восьми членов модели рангового распределения Х29 первые два образуют тренд, у которых период колебания стремится к бесконечности. Первый член является законом Мандельброта (в физике), Лапласа (в математике), Перла-Ципфа (в биологии) и Парето (в эконометрике). Второй кризисный член является степенной функцией. Остальные пять вейвлетов имею сильную адекватность выше 0.7.  

После восьмого члена максимальная относительная погрешность равна всего 0.29%. Тогда 14 субъектов федерации имеют между собой сильнейшую функциональную связность по коэффициенту миграционного прироста. Получается, что коэффициент миграционного прироста дает колебательные связи с высокой точностью, получающие сильное фрактальное распределение.

Для сопоставления парных отношений по возможностям CurveExpert-1.40 приняты по три составляющие общей модели вейвлета. Три пары влияния на миграционный прирост имеют коэффициент корреляции не менее 0.95 (сверхсильные факторные связи). Например, Тренд влияния восточной долготы на миграцию содержит два члена. Первый является постоянным членом в -20.43204 чел. и это характеризует среднестатистическую интенсивность миграции для всех 14 субъектов Западной Сибири.

Предложенный метод анализа позволяет определять тесноту связи влияния выбранных параметров жизни как влияющих переменных на одну из них, например, коэффициент миграционного прироста как зависимый показатель. Амплитудно-частотный анализ выявленных трехчленных моделей позволяет определять рациональные интервалы изменения тех или иных параметров. В итоге появляется возможность оптимизации всех 40 параметров жизни для повышения притока населения в субъекты федерации Западной Сибири.