Исследование ориентации частиц в агломератах, смоделированных с помощью двумерных моделей

Введение

Свойства поликристаллического материала, особенно связанные с механической анизотропией, сильно зависят от микроструктуры [1]. При образовании агломератов плотность упаковки частиц варьируется от области к области образца. Однако распределение порошка имеет важное значение для определения механизмов уплотнения, особенно в тех случаях, когда напряжение играет важную роль, например, при спекании под высоким изостатическим давлением (HIP).На характеристики текучести очень мелких частиц также влияет агломерация частиц.

Чтобы обеспечить свободное движение зерен, эти частицы обычно агломерируют до воспроизводимых форм и размеров с помощью подходящего метода грануляции [2]. Несмотря на высокую распространенность систем, в которых происходит та или иная форма агломерации, механизмы, управляющие их образованием и зависящие от сил между частицами, агломератами и стенками контейнера, в целом мало изучены [3]. Частично это связано с отсутствием лабораторных приборов для их адекватной характеристики, а также с высокими вычислительными мощностями, необходимыми для учета взаимодействий миллионов частиц и кластеров с зачастую неоднородными свойствами.

Даже когда первичные частицы имеют сферическую форму и одинаковые размеры, в зависимости от типа обработки и задействованных сил агломераты могут иметь преимущественную ориентацию частиц. Традиционные методы измерения ориентации зерен в поликристаллических материалах, такие как роза пересечений [4], например, при применении непосредственно к структурам кластерного типа, не идентифицируют никаких направлений. Эти кластеры часто описываются как фракталы и имеют фрактальные размеры, меньшие, чем их евклидова размерность [3]. Цель данной работы двоякая: разработать простую имитационную модель двумерной агломерации частиц таким образом, чтобы полученную структуру можно было полностью охарактеризовать; и реализовать новый метод оценки ориентации структуры, образованной частицами в агломерате.

Экспериментальная часть

Группы слабосвязанных частиц могут вести себя как более крупные псевдочастицы, называемые кластерами. В случае чрезвычайно мелких керамических порошков плотность упаковки обычно очень низкая. Одна из возможных причин этого состоит в том, что основными единицами упаковки являются твердые агломераты (агрегаты низкой плотности, образующиеся при синтезе порошков), рост которых происходит за счет накопления в случайных положениях мелких частиц при броуновском движении вокруг исходное ядро. Данные литературы свидетельствуют о том, что такие агрегаты самоподобны с увеличением размеров и поэтому ведут себя как фракталы.В данной работе для геометрического моделирования кластеров частиц использовался очень простой алгоритм: сферы притягиваются из случайных положений, вокруг сферу, расположенную в центре двумерного контейнера заранее заданных размеров (здесь называемого центром зародышеобразования), пока они не достигнут другой сферы [5].Эта процедура моделирует ситуацию, когда между частицами действуют силы притяжения (силы Вана дер Ваальса или электростатики, например), которые отвечают за прерывание движения каждой частицы. На рисунке 1 представлен двумерный кластер, смоделированный с помощью этого алгоритма.

Рисунок 1: двумерный кластер, смоделированный в вычислительной среде и моделировании твердых тел.

Моделирование проводилось в среде компьютерной графики с возможностями твердотельного моделирования. Использование этой среды, помимо возможности позиционирования и визуализации объектов с помощью существующих функций, позволяет реализовать конкретные алгоритмы движения и взаимодействия между частицами посредством программирования на языках высокого уровня, таких как LISP или C.

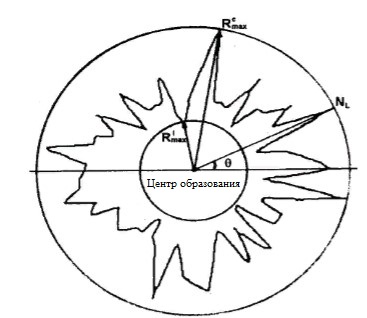
Рисунок 2: Радиальная ориентация моделируемого двумерного кластера, полученная с использованием центра зарождения кластера в качестве эталона.

Ориентация в кластере

Можно получить распределения ориентаций линий или поверхностей, например, ориентации границ зерен, краев зерен, фазовых границ и т. д. Следует отметить, что ориентации элементов микроструктуры могут отличаться от предпочтительных ориентаций кристаллов. Хотя преференциальную ориентацию в кристаллическом смысле можно понимать, как глобальное свойство, до сих пор не предложено способа выражения предпочтительной ориентации через какой-либо конкретный параметр [1]. Один из способов визуализировать распределение ориентации — через розу точек пересечения [4]. . Чтобы построить его в систему линий с осью ориентации, просто нарисуйте под микроскопом серию параллельных секущих, образующих угол, определяемый как ось ориентации. Затем определяется количество пересечений на единицу длины NL для этого конкретного угла. Процесс повторяется во всех направлениях плоскости. Затем график θ x NL рисуется в полярных координатах, а радиусы соединяются плавными кривыми, получая известную розу пересечений. Для изометрической системы (без ориентации) роза точек пересечения, согласно описанной процедуре, будет представлять собой круг с центром в начале полярной системы. Применяя этот традиционный метод измерения ориентации частиц к моделируемому кластеру, можно было сделать вывод, что в этом случае не будет никакой преимущественной ориентации. Необходим другой подход, чтобы принять во внимание радиальные ориентации, подобные тем, которые обнаружены в моделируемом скоплении. Эта работа предлагает альтернативный способ измерения ориентации, принимая центр зародышеобразования в качестве эталона для полярной системы координат. Предлагаемый метод включает определение количества точек пересечения на единицу длины луча с началом в центре зарождения кластера в ряде n направлений.

Таким образом, с шагом 2мк/н радиан получают значения NL для каждого направления и строят график θ x NL в полярных координатах. На рисунке 2 показан график, полученный для моделируемого кластера рисунке 1 для n = 64 после соединения спиц огибающей. Этот метод был реализован в микроструктурном анализаторе изображений Quantikov [6]. Анализируя график, представленный на рисунке 2, можно отметить, что моделируемый кластер представляет большое количество осей ориентации, характеризующихся направлениями с наибольшими радиусами. Можно определить степень ориентации для каждого направления θ, ω_θ, например, где R_θ — значение радиуса (NL) угла, а Rⁱ_max — радиус наибольшего круга на диаграмме с центром в начале полярной системы.

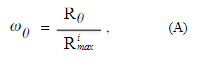
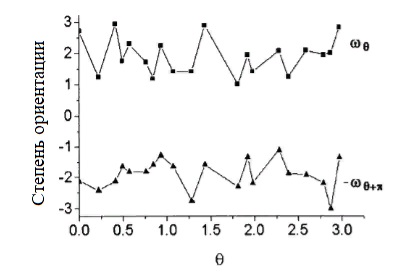
Рисунок 3: Изменение степени ориентации (ω_θ и −ω_θ+π) для радиальной ориентации θ, в радианах, для моделируемого кластера.

Согласно этому определению значения ωθ будут варьироваться от 1 (R_θ = Rⁱ_max) до максимального значения ωθmax, определяемого формулой где Rⁱ_max — наибольшая описанная окружность на диаграмме с центром в начале полярного начала. Построение на одном и том же графике в независимых кривых декартовых координатах для ω_θ и - ω_θ+π в зависимости от угла θ, в интервале 0≤ θ ≤ µ рисунке 3), помимо радиальных ориентаций, выявило области с одной ориентацией Ось можно определить, просто оценив площадь между двумя кривыми. Области с площадями значительно выше других могут характеризовать регионы с единственной осью ориентации.

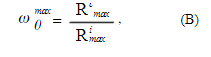
Фрактальные характеристики кластера

Фрактальные характеристики смоделированного двумерного кластера после некоторых операций морфологического замыкания и прореживания с использованием программного обеспечения Quantikov [6] были проанализированы через Интернет с использованием программного обеспечения FRACTOP V0.1 [7]. Это «программное обеспечение» использует метод, основанный на накоплении массы, для исследования фрактальной зависимости. На рисунке 4 показано изменение массы в зависимости от радиуса кластера, измеряемого в количестве пикселей. Отмечено, что масса кластера растет до радиуса примерно 160 пикселей, затем начинает уменьшаться, достигая примерно 280 пикселей, когда достигается максимальный радиус кластера. Для стимулирования фрактальной зависимости используется логарифмический график изменения накопленной массы кластера в зависимости от его радиуса (Ф.Д. – «Фрактальная зависимость» на рисунке 5). По наклону прямой, соответствующей кривой, видно, что кластер ведет себя как фрактал размером 1,695 вплоть до радиуса примерно 160 пикселей.

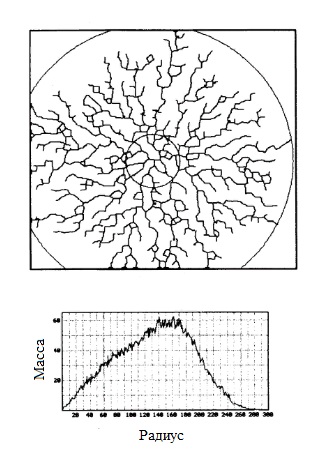
Рисунок 4: Изменение массы в зависимости от радиуса моделируемого двумерного кластера, измеренное в количестве пикселей.

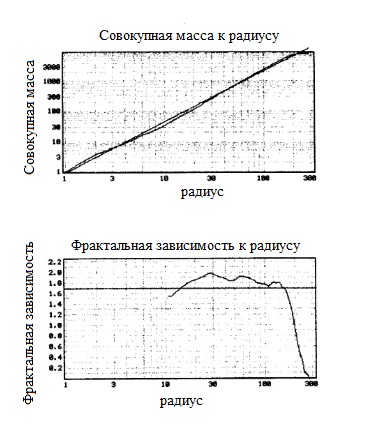
Рисунок 5: Изменение накопленной массы кластера в зависимости от его радиуса, используемое для оценки фрактальной зависимости.

Заключение

Применение традиционного метода получения распределений ориентаций в моделируемом кластере в среде графических вычислений и твердотельного моделирования не выявило каких-либо предпочтительных ориентаций. Применение метода, предложенного в этой работе и реализованного в анализаторе микроструктурных изображений Quantikov, идентифицировало радиальную ориентацию моделируемого кластера посредством позиционирования полярной системы координат в его центре зарождения. Использование заданной степени ориентации служит не только для получения радиальных направлений, но и для определения других возможных осей ориентации. Эта же концепция, примененная к структурам без ориентации или ориентированным по одной или нескольким осям ориентации, дает результаты, аналогичные тем, которые получаются обычным методом получения розы пересечений. Интерпретация этих кластеров в соответствии с фрактальными представлениями привела к определению значения фрактальной зависимости 1,695. Необходимы дополнительные исследования, чтобы попытаться связать фрактальные характеристики этих кластеров с графическими закономерностями, полученными новым методом.