Экспериментальная валидация моделей адсорбционного слоя с цеолитами 5А используемых для покрытий микродугового оксидирования

Введение

Процессы адсорбционного разделения используются в промышленности вместо обычных технологий. В адсорбционных слоях степень сжатия частиц, радиальное распределение пористости и связность пор, образующихся между адсорбирующими частицами, непосредственно влияют на процессы тепло- и массопереноса [1]. Стеновые эффекты являются важными факторами при анализе и проектировании адсорбционных слоев. Радиальное изменение пористости существенно влияет на профили температуры и скорости в пластах. Модели, используемые для прогнозирования радиального распределения пористости, обычно очень упрощены и не предусматривают демпфированных перепадов радиальной пористости или частиц разного размера [2,3]. Так что часто значения, предсказанные этими моделями, не соответствуют экспериментальным значениям. Определение координационного числа частиц и связности пор требуют реализации последовательных сечений и мониторинга вариаций топологических свойств каждого элемента от одного участка к другому [4]. Это требует много времени и усилий, что затрудняет прогнозирование важных параметров разделения газа через адсорбционные слои, таких как проницаемость. Органический или неорганические барьерные слои обычно наносятся для эффективного контроля скорости коррозии применяемых алюминиевых сплавов, что позволяет избежать возникновения катодной реакции [4]. Целью этой работы является разработка геометрического моделирования для адсорбционного слоя с 5A цеолитными частицами, посредством реализации моделей сжатия частиц в среде графических вычислений и твердотельного моделирования (AutoCAD). Эти модели используются после соответствующих этапов проверки в качестве средства определения параметров трудного экспериментального доступа.

Экспериментальная часть

Измерение распределения по размерам коммерческих цеолитных частиц 5А, выполненное путем просеивания гранулометрического разделения, ясно показывает, что распределение является бимодальным, с присутствием частиц со средним диаметром 2,41 мм и мелких частиц со средним диаметром 1,68 мм в соотношении 20 мас % и 80 мас % соответственно. Форма частиц очень близка к сферической, но некоторые частицы разрушены, как можно видеть на рисунке 1. Эти частицы будут использоваться в пилотном блоке разделения газа, сконструированном и установленном на CDTN. Установка состоит из адсорбционного слоя из нержавеющей стали диаметром 25 мм и высотой 400 мм, содержащего цеолиты типа 5А, электромагнитный клапан, управляемый таймером и устройствами для измерения давления, температуры и расхода. Плотности адсорбционных слоев, измеренные гравиметрическим методом, составляли: 0,96 г/см3 для слоя, заполненного большими и малыми сферами, в пропорции 20 мас % и 80 мас % соответственно; 0,93 г/см3 для слоя, заполненного только большими сферами; 0,90 г/см3 для слоя, заполненного только маленькими сферами. Известно, что на радиальное распределение пористости в слоях со сферами одинакового размера, распределенными случайным образом, влияет близость к стенкам контейнеров. Первый слой, находящийся в контакте со стенкой, имеет тенденцию быть полярным, причем большинство сфер касается стенки. Ближе к центру установки, слои имеют тенденцию быть все более и более неупорядоченными, пока, вдали от стены, не будет получена совершенно случайная конфигурация. Исследования, проведенные в этой области и опубликованные с 1958 года, ясно показали, что эти распределения радиальной пористости колеблются затухающим образом от центра системы.

Параметр, который в значительной степени влияет на радиальное распределение пористости, представляет собой соотношение между диаметром слоя и диаметром сфер. Для очень больших значений соотношения сторон (выше 20) , колебания имеют диапазон от четырех до пяти диаметров сфер от стенки слоя. Сферы с соотношениями сторон менее 10 не имеют никаких областей с постоянными пористостями. На основе этих экспериментальных наблюдений были разработаны некоторые эмпирические модели, относящиеся к радиальной пористости к соотношению сторон и расстоянию стенки [2,4]. Эти модели использовались в аналитических транспортных моделях для моделирования уплотненных слоев сферических частиц в цилиндрических контейнерах. Их результаты будут полезны в качестве косвенных методов для проверки используемых моделей моделирования.

Рисунок 1: Коммерческие цеолитные частицы 5А производства Bayer

Для моделирования слоя цеолита был реализован вычислительный алгоритм, в котором сферические частицы падают из случайного положения верхней части цилиндрического слоя. При его падении каждая частица достигает устойчивого положения, когда происходит одно из следующих: достижение дна подложки; достичь двух частиц и стенки слоя; и достигают трех других частиц одновременно. В некоторых конкретных случаях в последних двух представленных ситуациях частицы могут еще не находиться в стабильном положении и должны продолжать процесс падения [5,6]. Также реализованы алгоритмы, допускающие перемещение сфер в нижней части цилиндрического слоя, когда они достигаются некоторой сферой в процессе падения. Эти критерии устойчивости проиллюстрированы на рисунке 2 и зависят в основном от вертикальной полупрямой m, которая проходит через центр движущейся сферы М.

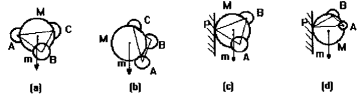
Рисунок 2: Критерии устойчивости для сферы, контактирующей с тремя другими или двумя сферами и стенкой (стабильные a и c и нестабильные b и d).

Если m пересекает внутреннюю часть треугольника, образованного центром трех сфер. (А, В и С) или две сферы и точка Р контакта со стенкой, М будут стабильными. В противном случае М будет нестабильным. Смоделированный трехмерный адсорбционный слой с использованием этих критериев для сферических частиц того же размера показан на рисунке 3.

Рисунок 3: Имитация трехмерного адсорбирующего слоя всреде компьютерной графики.

Было проведено сравнение объемных долей пор (V ^p_v), измеренных в моделируемых слоях с использованием описанных алгоритмов, и долей, измеренных в реальных слоях с использованием гравиметрических методов (таблица 1).

Таблица 1: V ^p_v в реальном слое и моделируемом слое с (а) алгоритмом, который не учитывает движение частиц на дне слоя, и (b) алгоритмом, который учитывает движение частиц на дне слоя.

Значения, полученные для V ^p_v с помощью алгоритма моделирования, который учитывает перемещение частиц на дне слоя, ближе к значениям, измеренным для реальных слоев, что делает этот алгоритм моделирования наиболее подходящим для представления анализируемого слоя цеолита. Для моделируемого слоя с двумя размерами частиц измеряли радиальное распределение пористости.

Обратите внимание на наличие демпфированных колебаний, предусмотренных моделями, которые учитывают один размер частиц, однако с дифференцированными характеристиками по отношению к амплитудам и периодам, вызванными наличием двух размеров. [7,8]

Реализация последовательных сечений в образцах реальных пластов, помимо возможности проверки оценочных значений радиального распределения пористости и связности, позволяет непосредственно оценить стереометрические методы, такие как метод Салтыкова. Это возможно, поскольку распределение частиц по размерам, полученное из секции, можно сравнить с распределением частиц по размерам, оцененным с помощью последовательных секций. 12 последовательных срезов выполняли в образце слоя, содержащего крупные цеолитные частицы 5А, и измеряли для каждого толщину слоя с помощью микрометра. Каждую секцию сканировали непосредственно в сканере с разрешением 600 dpi и печатали в прозрачном виде, чтобы каждая цеолитная сфера могла сопровождаться последовательными секциями с целью определения ее диаметра и координат ее центра. Диаметр каждой сферы оценивался по диаметрам двух ее сечений в последовательных секущих плоскостях. Для определения координационного числа сфер в секционированном участке образца слоя в графической вычислительной среде с твердотельным моделированием позиционировали 254 сферы с диаметрами и координатами, определяемыми последовательными участками. Сравнение распределения координационных чисел, полученных для моделируемого слоя, со сферами одинакового размера со значениями, полученными для образца реального слоя, показано на рисунке 4.

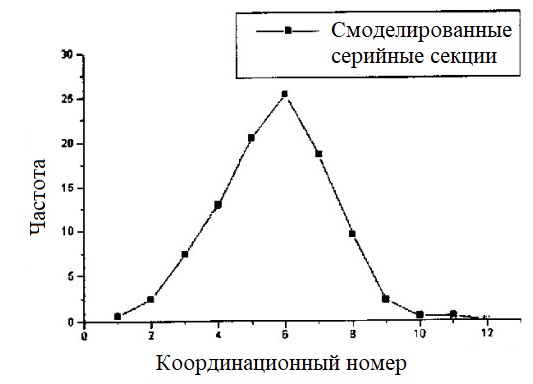
Рисунок 4: Сравнение координационных чисел частиц в моделируемом адсорбирующем слое и фактическом слое

Среднее большее координационное число реальной частицы (6,2 для реальной частицы и 5,7 для моделируемой частицы) можно объяснить более низкой объемной долей этого по сравнению с моделируемым слоем (39,2% по сравнению с 43,0%) и за то, что для моделирования были использованы сферы одинакового размера, а не распределение «реальных» размеров, определенное в используемых цеолитах 5А.

Однако ошибка в оценке связности слоя с использованием результатов моделирования составляет менее 9%, что делает их подходящими для большинства применений, особенно если считать, что это параметр трудного экспериментального доступа. Сплющивание кривой распределения координационных чисел, полученной по методике сериализованных сечений на их концах, обусловлено тем, что имеется диапазон диаметров сфер, вместо единого размера, как это рассматривается при моделировании. Эффект введения более крупных частиц в набор более мелких частиц такого же размера, например, заключается в увеличении частоты больших координационных чисел, соответствующих введенным более крупным частицам, которые окружают себя большим числом более мелких частиц. Это приводит к распрямлению кривой с правой стороны. Кроме того, более мелкие частицы, контактирующие с более крупными частицами, будут иметь тенденцию к уменьшению их координационных чисел, что также приведет к сплющиванию кривой влево. Изменение диаметра, поскольку оно влияет на отношение размеров, также по-разному влияет на координационное число частиц, близких к стенкам реального слоя, относительно моделируемого слоя, который учитывает один размер частиц.

Заключение

По результатам, полученным из объемных долей пор и средних координационных чисел частиц, для моделируемых слоев и фактических слоев были обнаружены различия между результатами, полученными для этих двух переменных ниже 10%. Это указывает на то, что реализованные алгоритмы расчетного геометрического моделирования могут быть использованы для прогнозирования свойств и конструкции адсорбционных слоев. Радиальные распределения пор, полученные моделированием, соответствуют тем, которые предсказаны аналитическими моделями, и результатам, полученным из последовательных сечений. Затем может быть установлена процедура для определения радиального распределения пористости и связности со слоями цеолита 5А, принимая за основу реализованные алгоритмы моделирования.