РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ СИСТЕМЫ ОДУ

ВВЕДЕНИЕ       

Обыкновенные дифференциальные уравнения широко используются для математического моделирования процессов и явлений в различных областях науки и техники. Множество переходных процессов в радиотехнике, кинетика химических реакций, динамика биологических популяций, движение космических объектов, модели экономического развития исследуются с помощью обыкновенных дифференциальных уравнений. Задача Коши в свою очередь является одной из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Актуальность темы научно-исследовательской работы состоит в том, что ОДУ имеют аналитически сложное решение и разработка программы, решающей задачу коши одним из методов Рунге-Кутты, может облегчить с дифференциальными уравнениями.

В научно-исследовательской работе исследуется разработка программы поиска решения системы дифференциальных уравнений методам Рунге-Кутта и анализ полученных данных с помощью нее.

Задачей данной научно-исследовательской работы является упрощение работы с ОДУ в виде ускорения вычислений для последующей работы с ними.Для этого подойдет метод Рунге-Кутта. Выбор метода решения системы дифференциальных уравнений объясняется тем, что метод Рунге-Кутта сочетает хорошую точность и высокую скорость.

РЕШЕНИЕ ЗАДАЧИ КОШИ ДЛЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МЕТОДОМ РУНГЕ-КУТТА

Для решения задачи Коши для ОДУ существуют несколько способов. В данной научно-исследовательской работе будут представлены некоторые из них.

Постановка задачи Коши для систем обыкновенных дифференциальных уравнений

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при {\displaystyle t=0}t = 0, а решение отыскивается при t>0{\displaystyle t>0}TT.

В данной научно-исследовательской работе будет рассмотрен метод Рунге-Кутта для дифференциальных уравнений 4 порядка.

Метод Рунге — Кутты четвёртого порядка при вычислениях с постоянным шагом интегрирования столь широко распространён, что его часто называют просто методом Рунге — Кутты.

Задача Коши заключается в решении систем обыкновенных дифференциальных уравнений первого порядка, представляемых в виде:

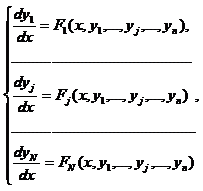                   (1.1)

где j=1N-номер каждой зависимой переменной y_j, x-независимая переменная .

Решение системы (1) при заданных начальных условиях

x=x₀,

                           y₁(x₀)=y_10В,…,           (1.2)

y₂(x₀)=y₂₀,

y_N(x₀)=y_N0

сводиться к нахождению зависимостей (интегральных кривых) y₁(x),…,y₂(x), y_N(x), проходящих через точки (x₀,y₁₀), (x₀,y₂₀),…, (x₀,y_N0). Задача Коши сводиться к интегрированию дифференциальных уравнений. Порядок метода численного интегрирования при этом определяется и порядок метода решения.

Метод Рунге-Кутты для решения ОДУ четвертого порядка

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка.

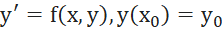
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

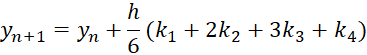                                                     (1.3)

Вычисление нового значения проходит в четыре стадии:

,

 

   ,

 ,

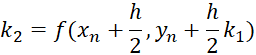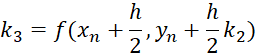                                            ,                              (1.4)

где{\displaystyleh}h — величина шага сетки по {\displaystylex} x.

Этот метод имеет четвёртый порядок точности. Это значит, что ошибка на одном шаге имеет , а суммарная ошибка на конечном интервале интегрирования имеет порядок  .

Многошаговые методы решения задач Коши для ОДУ

Методы решения ОДУ бывают одношаговые и многошаговые. К одношаговым относятся: метод Эйлера, метод Рунге – Кутты и др., а к многошаговым: линейные многошаговые разностные методы, в том числе методы Адамса-Башфорта и методы Адамса-Мултона.

В многошаговых методах повышение точность вычисления происходит за счет использования информации о поведении решения на предыдущих шагах.

Общая схема построения m-шаговых разностных методов, используемых для приближенного решения задачи Коши

                                                                                    (1.4)

выглядит следующим образом

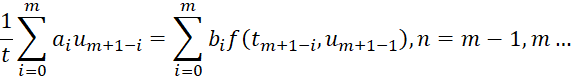          (1.5)

где a_i,b_i- числовые коэффициенты, не зависящие от n, причем . Уравнение следует рассматривать как рекуррентное соотношение, выражающее новое значение  через найденные ранее значения. 

Наиболее простые и наиболее часто встречающиеся вычислительные правила для многошаговых методов имеют вид:

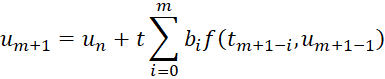                                             (1.6)

Среди правил особенно широко известны явные (экстраполяционные) при b₀=0 и неявные (интерполяционные) при b₀=1 методы Адамса.

Параллельные методы численного решения задачи Коши для ОДУ

В данной главе будут рассмотрены основы распараллеливания одношаговых и многошаговых алгоритмов методов решения задачи Коши для ОДУ.

Для простоты понимания и вывода формул, будем рассматривать решение задачи Коши для одного обыкновенного дифференциального уравнения первого порядка (1.4).

Множество M точек равномерной сетки { t m }, m = 1,M и t m =T с шагом 1 разобьем на N блоков, содержащих к точек каждый, при этом k NхM. В каждом блоке введем номер точки i = 0,k и обозначим через t n , i точку n блока с номером i. Точку t n ,0 назовем началом блока n, а t n , k - концом блока. Очевидно, что имеет место t n , k = t n +1,0 . Условимся начальную точку t 0 = t 1,0 в блок не включать. При численном решении задачи Коши для каждого следующего блока новые k значений функции вычисляются одновременно. Поэтому блочные методы особенно удачно реализуются на параллельных вычислительных системах.

ИССЛЕДОВАНИЕ МЕТОДА РУНГЕ-КУТТЫ ДЛЯ РЕШЕНИЯ ОДУ ЧЕТВЕРТОГО ПОРЯДКА.

В данной научно-исследовательской работе будет исследоваться метод Рунге-Кутта, так как данный метод является достаточно несложным в реализации, но в то же время достаточно точным.

Разработка блок-схемы решения задачи Коши для обыкновенных дифференциальных уравнений методом Рунге-Кутта.

В качестве входных данных к этому методу потребуется ввести само дифференциальное уравнение с начальной точкой y(0) и параметром h отвечающим за шаг счетчика

Таблица 1 – описание переменных

П\п	Обозначение	Тип	Наименование
1	H	Входное значение	Счетчик шага
2	X1	Входное значение	Массив со значениями переменной х
3	Ur	Входное значение	Задаваемое уравнение
4	Y1	Входное значение	Начальное значение у(0)
5	X	Промежуточное значение	Переменная х
6	Y	Промежуточное значение	Переменная у
7	K1	Промежуточное значение	Значение получаемое при подставленииx и y в уравнение
8	K2	Промежуточное значение	Значение получаемое при подставленииx и y в уравнение
9	K3	Промежуточное значение	Значение получаемое при подставленииx и y в уравнение
10	K4	Промежуточное значение	Значение получаемое при подставленииx и y в уравнение

Рисунок 1 – Блок-схема

Листинг программы:

clc;

clear;

ur='cos(x+y)+0.5*(x-y)';

h=0.1;

x1=[0:h:1];

y1(1)=0;

for

i=1:1:length(x1)-1

x=x1(i);

y=y1(i);

k1(i)=eval(ur);

x=x1(i)+h/2;

y=y1(i)+h*k1(i)/2;

k2(i)=eval(ur);

y=y1(i)+h*k2(i)/2;

k3(i)=eval(ur);

x=x1(i)+h;

y=y1(i)+h*k3(i);

k4(i)=eval(ur);

y1(i+1)=y1(i)+h*(k1(i)+2*k2(i)+2*k3(i)+k4(i))/6;

end

plot(x1,y1);

Проверка алгоритма на практике и анализ точности вычисления

Для проверки правильности и точности программной реализации метода Рунге-Кутта были выбраны несколько уравнений:

 

1. 
2. 
3. 

Для проверки результатов вычисления следует решить их в общем виде и сравнить с ответами полученными методом Рунге-Кутта.

1. 
2. 
3.  

Рисунок 2 – Решение линейной формы первого уравнения для проверки

 

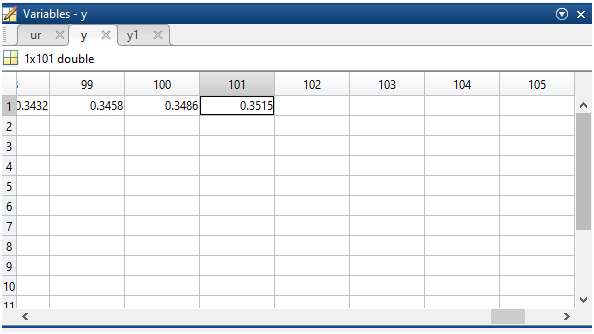
Рисунок 3 - Решение дифференциальной формы первого уравнения для проверки

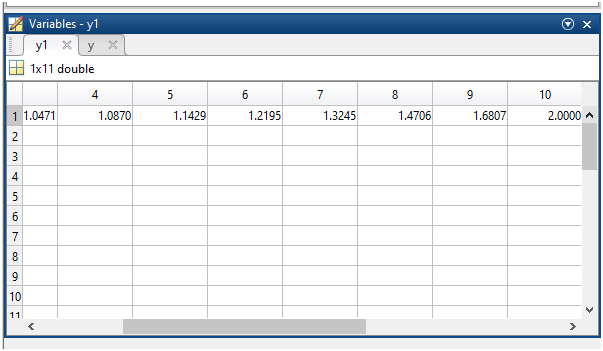
Рисунок 4 - Решение линейной формы второго уравнения для проверки

 

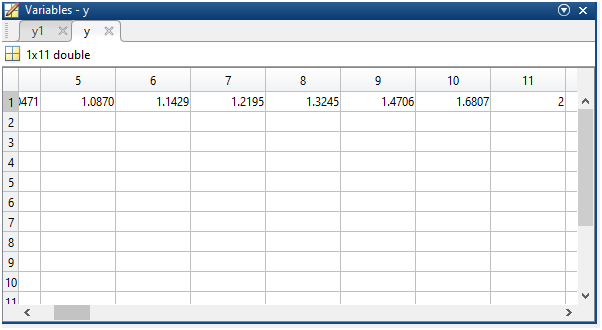
Рисунок 5 - Решение дифференциальной формы второго уравнения для проверки

 

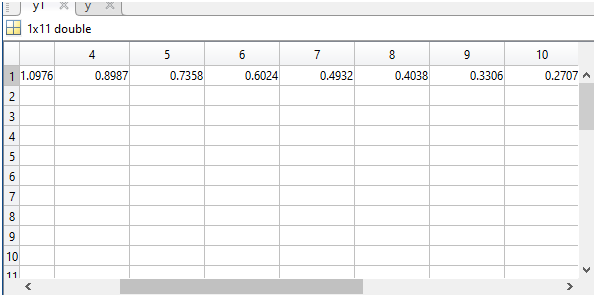
Рисунок 6 - Решение линейнойформы третьего уравнения для проверки

 

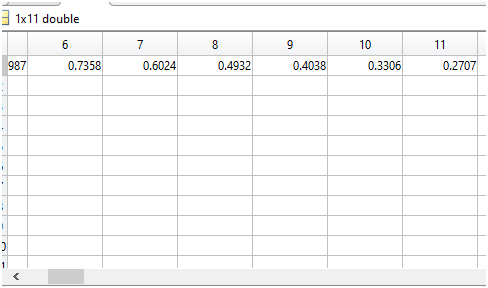
Рисунок 7 - Решение дифференциальной формы третьего уравнения для проверки

          При построении графиков для полученных значений оба графика накладываются полностью друг на друга:

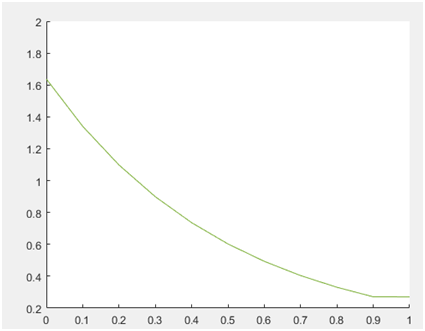
Рисунок 7 – Графики x,yи x1,y1

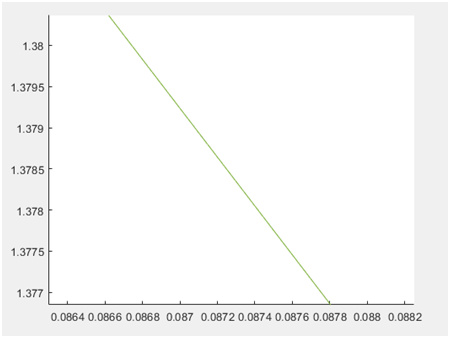
Рисунок 7 – Графики x,yи x1,y1 (приближенные)

Отсюда следует что при решении методом Рунге-Кутта и при решении дифференциального уравнения общего вида стандартным решением значения полученные в результате работы являются очень близкими друг к другу. Из этого следует вывод, что метод Рунге-Кутта является очень точным и достаточно простым в программной реализации.

ЗАКЛЮЧЕНИЕ

В данной научно-исследовательской работе был рассмотрен и реализован в программе метод решения ОДУ Рунге-Кутта. В ходе выполнения работы было выявлено что этот метод является достаточно точным и быстрым. Все три подобранных примера показали один и тот же результат – при каждом вычислении погрешность составляла меньше 0.0001. В таком случае можно сказать что поставленная задача по программной реализации быстрого и точного метода прошла успешно.

Программа, реализованная в среде MATLAB, показала хорошую работоспособность и точность в вычислениях. Результаты полученные в ходе ее работы показывают, что задача приближенного решения ОДУ была успешно выполнена.