СВЯЗЬ МАТЕМАТИКИ И ГЕОГРАФИИ

Математика тесно связана со многими науками, ведь это фундаментальная область, пронизывающая все сферы нашей жизни. Стремительное развитие наук ведет к неиссякаемому исследовательскому потенциалу, открывая перед нами новые горизонты знаний. К каждой конкретной дисциплине можно подойти с бесчисленными вопросами и возможностями для исследования. География, история, астрономия, социология, психология – все они помогают нам расширять наше понимание окружающего мира. Так, математика и другие науки идут рука об руку, вместе дополняя друг друга и расширяя границы человеческой эрудиции. Они позволяют нам лучше понимать, объяснять и изменять мир вокруг нас. Благодаря этим наукам мы можем открыть для себя новые горизонты и преодолеть самые сложные вызовы, что делает их поистине незаменимыми компаньонами человечества в его стремительном развитии.

Более подробно рассмотрим связь математики и географии, которая существует на множестве уровней и играет важную роль в понимании и изучении нашей планеты. Математика предоставляет географии инструменты для анализа, моделирования и прогнозирования различных географических явлений.

Одним из наиболее очевидных примеров является картография – наука о создании и изучении карт. При создании карт необходимы математические методы и концепции для корректного представления географической информации. Например, проекции позволяют преобразовывать трехмерную поверхность Земли в двумерное представление на карте. Различные классификации и системы координат также широко используются в картографии.

Другим примером связи между математикой и географией является геостатистика. Эта наука занимается анализом и предсказанием пространственного распределения различных физических и географических явлений, таких как климат, засухи или загрязнение воды. Геостатистические методы и модели используются для работы с географическими данными и извлечения полезной информации из них.

Математическое моделирование также играет важную роль в географии. Оно позволяет анализировать и предсказывать сложные географические процессы и явления, такие как распределение населения, потоки транспорта или изменение ландшафтов. Математические модели позволяют исследовать взаимодействие различных факторов и оценивать их влияние на географическую среду.

Рассмотрим на примере, как математика используется в географии. Задание: определите по карте расстояние на местности по прямой от точки А до колодца. Измерение проводите между точкой и центром соответствующего условного знака. Полученный результат округлите до десятков метров. Ответ запишите в виде числа.

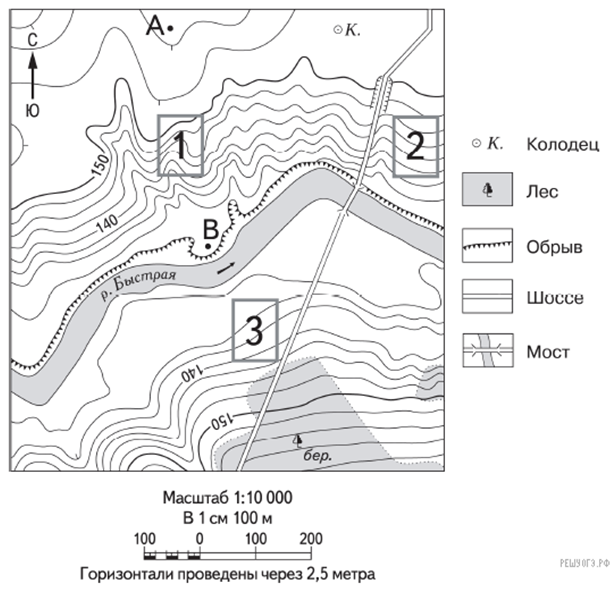
Рисунок 1. Карта к заданию

Пояснение. В 1 см карты — 100 метров, поэтому что бы получить ответ в метрах, расстояние между пунктом А и колодцем, измеренное в сантиметрах, необходимо умножить на 100. Однако на экране монитора карта могла измениться в размерах. Поэтому следует найти, во сколько раз расстояние между заданными точками больше длины масштабного отрезка, а затем полученное отношение умножить на 100. Допустим, на мониторе длина масштабного отрезка 1,1 см. На мониторе длина от точки А до колодца равна 3,4 см, длина масштабного отрезка 1,1 см. Поэтому следует найти, во сколько раз расстояние между пунктом А и колодцем больше длины масштабного отрезка, а затем полученное отношение умножить на 100. Расстояние равно 3 отрезкам или 300 метрам. Имеем (3,4 : 1,1) · 100 = 309 м. Округлим: 310.

 Ответ: 300|310|320.

Таким образом, математика и география тесно связаны и взаимодействуют друг с другом. Математические методы и концепции позволяют географам анализировать, понимать и объяснять различные географические процессы и явления, что способствует углубленному изучению нашей планеты. Вместе они образуют мощный инструментарий для исследования и понимания сложной географической реальности.