Развитие современного общества характеризуется повышением технического уровня во всех областях жизнедеятельности. Потребность управления различными процессами приводит к использованию математического моделирования. Математичекое моделирование – это построение моделей, их исследование и прогнозирование результатов будущих наблюдений [1].
Построение модели достаточно сложный процесс и от правильности ее составления зависит дальнейшее исследование и вытекающие из этого исследования выводы и рекомендации.
Первым метод наименьших математических квадратов использовал Гаусс, а уже в 1805 году Лежандр смог независимо открыть и опубликовать это математическое направление.
Многие ученые пришли к выводу, что если некоторая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя при различных значениях
. В результате измерений получается ряд значений:
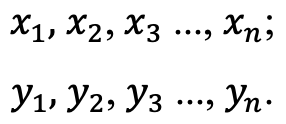
Таким образом, по данным некоторого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет один из методов математического моделирования - метод наименьших квадратов (МНК) [2].
Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой была наименьшей.
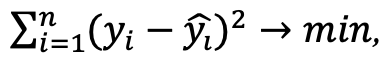
,
где - исходное значение, а
- рассчетное значение.
На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда можно построить уравнение вида
y = ax + b. (1)
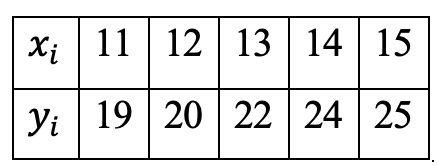
В результате исследования, были собраны статистические данные продажи телефонов за некоторый период (таблица 1).
Таблица 1 – Исходные данные
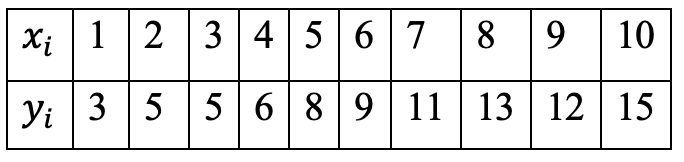
По исходным данным построено уравнение регрессии
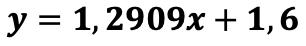 (2)
(2)
Определим по полученной модели несколько прогнозных значений (таблица 2).
Таблица 2 – Прогнозные значения
По прогнозным значениям можно моделировать финансовые затраты и прогнозировать прибыль магазина [5].
Коэффициент корреляции равен :
Значение линейного коэффициента корреляции, равное 0,21 говорит о том, что связь прямая (так как он положительный), и связь слабая. Это означает, что на значения могут влиять еще другие факторы (такие как, дни распродаж, появление новых моделей телефонов, скидки, акции и др.) [3].
Значение ошибки аппроксимации равно: . Это говорит о достаточно точном подборе линейной зависимости, что позволяет использовать построенную модель для исходной задачи [4].
Вывод: В ходе исследования подобрано уравнение регрессии, которое наиболее близко описывает процесс продаж. По построенной модели можно рассчитать прогонозные значения на будущий период и проводить оптимизацию финансовых затрат и прибыли.
Список литературы
- Колесникова С.В. Статистический анализ и прогнозирование тарифов и субсидий на услуги ЖКХ в регионе. Диссертация на соискание ученой степени кандитата экономических наук/Московский государственный университет экономики, статистики и информатики (МЭСИ). Москва, 2011.
- Колесникова С.В., Ковалерова Н.В. Статистический анализ ситуации на рынке жилья Пензенской области / региональная экономика: теория и практика, 2013. № 14. С. 60-64.
- Долгушева Л.Н., Дятков В.С., Колесникова С.В., Грушина Т.А. Разработка автоматизированной системы учета торговой деятельности предприятия . В сборнике: Информационные ресурсы и системы в экономике, науке и образовании. Сборник V Международной научно-практической конференции. 2015. С.36-40.
- Колесникова С.В., Экономические задачи, сводимые к транспортным задачам. В сборнике: Человек, общество и государство в современном мире. Сборник научных трудов международной научно практической конференции: в 2 томах. 2016. С.220-223.
- Шишов В.Ф., Колесникова С.В., Киндаева Е.Н., Современные инструменты статистического анализа и прогнозирования при решении прикладных задач. Территория инноваций. 2019. №2(30). С. 130-136.



