Применение общих алгоритмических методов при решении задачи кольцевого маршрута

В современном мире оптимизация алгоритмов является очень важной проблемой, так как системы должны обрабатывать все большие данные за меньшее время. Одной из известных задач является задача кольцевого маршрута, или же задача коммивояжёра. Цели данной статьи — оптимизировать решение задачи с помощью метода ветвей и границ, разработать алгоритм решения для задачи на языке С++, оценить количество переборов при решении задачи стратегией с помощью грубой силы и с разработанным методом.

Есть N городов, соединённых между собой дорогами. Необходимо проложить между ними кратчайший замкнутый маршрут, проходящий через каждый город только один раз. Расстояние из города j в город i считается неотрицательным числом: Dji ≥ 0. Часто Dji называют стоимостью ребра, так как дороги можно представить рёбрами, соединяющими города-вершины некоторого графа. Допускается несимметричность матрицы Dji ≠ Dji. В ещё более общем случае пути между некоторыми городами могут отсутствовать. Исходные условия можно записать в формате таблицы, где строки — города отправления, столбцы — города прибытия, в ячейках расстояния между ними.

Необходимые поля:

• Количество узлов;
• Массив минимального пути;
• Посещенные пути при текущем проходе;
• Вес минимального пути.

Необходимые методы:

• Начальный метод поиска пути;
• Рекурсивный метод построения пути для заданного начала (в качестве параметра);
• Первый минимум массива;
• Второй минимум массива;
• Сохранение пути.

Алгоритм начального метода поиска пути:

• Инициализация нижней границы (bound) по формуле 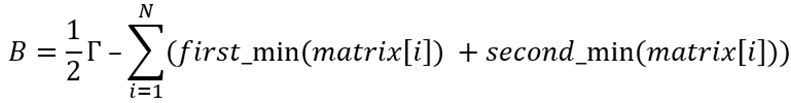1:

        (1)

где

B — нижняя граница;

N — количество узлов;

first_min — функция нахождения первого минимума в массиве;

second_min — функция нахождения второго минимума в массиве;

matrix — матрица маршрутом между узлами.

• Цикл вызова рекурсивного поиска минимального пути для каждого узла в качестве начальной точки

Алгоритм рекурсивного поиска пути

• Если все пройдено:
  • Если есть путь до начальной точки:
    • Длина пройденного пути = переданная длина + путь до начальной точки;
    • Если длина пути меньше минимальной длины:
      • Сохраняем путь и длину в качестве минимальных;
  • Завершаем метод;
• Иначе проходим по всем путям (i=0..N-1):
  • Если есть путь до не посещенной точки:
    • Сохраняем нижнюю границу;
    • Идем в узел i;
    • Добавляем к текущей длине пути;
    • Вычисляем нижнюю границу для текущего пути по формуле выше.
• Если текущая длина + граница для текущего пути меньше минимума:
  • Рекурсивный вызов следующего уровня (проходим в узел i);
  • Обрезаем узел;
  • Очищаем массив посещенных узлов.

В ходе тестирования метода ветвей и границ было совершено 30 генераций матриц и использован метод поиска пути для каждой из них. Результаты представлены в таблице 1. При использовании грубого метода использовалось: (10! вариантов путей) * (10 переходов на 1 путь) = 36 288 000 переходов.

Среднее количество переходов: 1328, что меньше грубого подхода в 27 325 раз. Результат отображен в таблице 1.

Таблица 1

Таблица количества переходов

Исследовав метод ветвей и границ, можно сделать вывод, что данный способ в разы превосходит по количеству итераций метод грубого перебора, несмотря на свою простоту в реализации.