В представленной теме анализируется решение задачи способом Ньютона.
Во первых, рассмотрим этап о границах существующих корней.
Выделяют часть способов их нахождения. Выделим основные.
Имеем полином 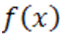 степени
степени 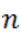 пусть
пусть 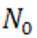 будет верхней границей его положительных корней. Представим полиномы:
будет верхней границей его положительных корней. Представим полиномы:
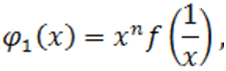
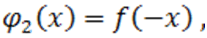
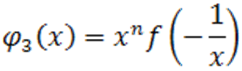
и вычислим верхние пределы их неотрицательных корней; допустим это будут соответственно числа 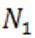 ,
, 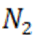 ,
, 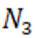 . Тогда все неотрицательные корни полинома
. Тогда все неотрицательные корни полинома 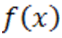 соответствуют неравенствам
соответствуют неравенствам 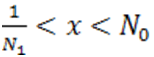 , все отрицательные корни
, все отрицательные корни  неравенствам
неравенствам 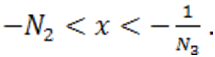
Для нахождения верхнего предела положительных корней можно использовать способ Ньютона.
Рассмотрим полином 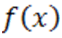 с действительными коэффициентами и неотрицательным старшим коэффициентом
с действительными коэффициентами и неотрицательным старшим коэффициентом 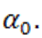 Если при
Если при 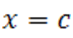 многочлен
многочлен 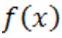 и все его последовательные производные
и все его последовательные производные 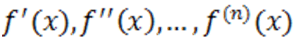 принимают положительные значения, то число
принимают положительные значения, то число 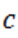 служит верхним пределом корней.
служит верхним пределом корней.
Пример. Используем способ Ньютона к многочлену 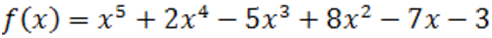 . Мы имеем:
. Мы имеем:
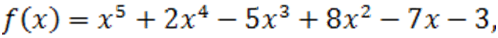
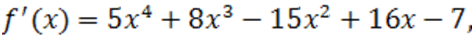
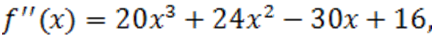
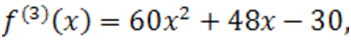
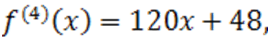
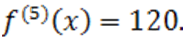
Данные полиномы неотрицательны при 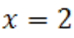 , что можно определить хотя бы схемой Горнера. Отсюда следует ,что число
, что можно определить хотя бы схемой Горнера. Отсюда следует ,что число 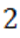 есть верхний предел положительных корней многочлена
есть верхний предел положительных корней многочлена 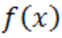 .
.
Рассмотрим полином 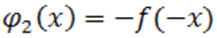 для определения нижнего предела отрицательных корней исходного полинома
для определения нижнего предела отрицательных корней исходного полинома 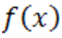 (мы берем
(мы берем 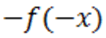 вместо
вместо 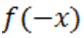 потому, что для использования способа Ньютона старший коэффициент должен быть неотрицательным, на корни полинома
потому, что для использования способа Ньютона старший коэффициент должен быть неотрицательным, на корни полинома 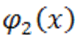 эта перемена знака не оказывает никакого влияния). Так как
эта перемена знака не оказывает никакого влияния). Так как
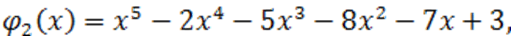
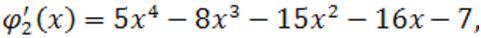
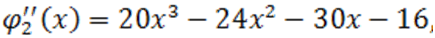
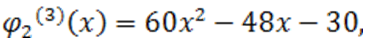
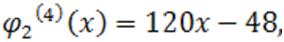
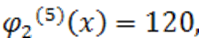
а данные полиномы больше нуля при 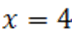 , то число
, то число 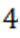 служит верхним пределом неотрицательных корней для
служит верхним пределом неотрицательных корней для 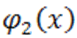 , и поэтому число
, и поэтому число 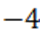 будет нижним пределом отрицательных корней для
будет нижним пределом отрицательных корней для 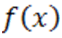 .
.
Анализируя, полиномы
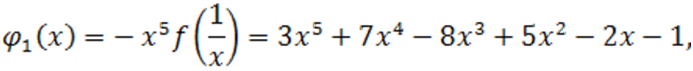
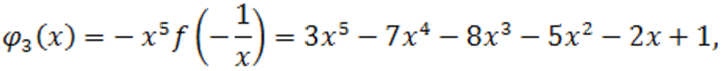
мы определим для них, используя способ Ньютона, в качестве верхнего предела неотрицательных корней соответственно числа 1 и 4, а поэтому нижним пределом положительных корней полинома 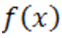 служит число
служит число 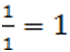 , верхним же пределом отрицательных корней
, верхним же пределом отрицательных корней  число
число 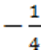 .
.
Следовательно, неотрицательные корни полинома 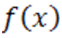 заключены между числами
заключены между числами 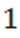 и
и 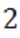 , отрицательные корни
, отрицательные корни  между числами
между числами 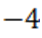 и
и 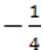 .
.
Заключение
Таким образом, система Штурма многочлена 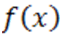 теряет по одной перемене знаков при переходе
теряет по одной перемене знаков при переходе 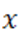 от
от 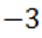 к
к 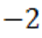 и от
и от 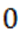 к
к 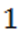 . Корни
. Корни 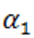 и
и 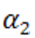 этого многочлена удовлетворяют, следовательно, неравенствам:
этого многочлена удовлетворяют, следовательно, неравенствам:
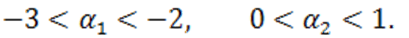
Список литературы
- Курош А.Г. Курс высшей алгебры. М.: Наука, 1965. – 431 с.
- Шафаревич И.Р. О решении уравнений высших степеней (метод Штурма), государственное издательство технико – теоретической литературы. Москва, 1954. – 24 с.



