ИСПОЛЬЗОВАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ ДЛЯ АНАЛИЗА И ОБРАБОТКИ ИНФОРМАЦИИ

    Введение.  В современное время человек не может представить себе жизнь без компьютера. Информационные технологи прочно вошли в быт людей и играют очень значимую роль в данное время.  Они очень крепко связаны и не могут теперь существовать друг без друга. И с каждым днем значимость только повышается. В связи с широким распространением  и использованием вычислительной техники способы оптимизации стали действенно использовать в самых всевозможных областях человеческой деятельности, и в основном, в данной области проектирования и анализа функционирования систем, анализа и обработки информации.

      В совокупности теория оптимизации дает собой некоторую совокупность математических методов, нацеленных на нахождение лучшего итога из большого количества альтернатив.

     При конструировании систем задача оптимизации объединяется к выбору этих значений параметров, характеризующих габариты подсистем, составляющих систему и режимы их работы, которым соответствует лучшее значение характеризующего показателя свойства функционирования системы.

      Наибольшее использование оптимизационные методы обнаружили в задачках инженерного анализа. В инженерной практике между более совокупных задач, образующихся в процессе разработки математических моделей, возможно отметить дилемму определения характеристик кое-какой эмпирической модели на базе данного большого количества опытных данных. Такового свойства задачки обработки информации или задачи регрессионного анализа методом легких преобразований приводятся к облику оптимизационных задач, потому что выбор значений характеристик модели исполнятся в согласовании с аспектом свойства описания имеющихся данных с поддержкой данной модели.

      Постановка задачи. Допустим, собственно, что кое-какая переменная y находится в зависимости от некоторой совокупности независящих переменных. Связующее между переменными обозначим уравнением y= f(x), при этом картина функции f нам не известен. Дабы отыскать надлежащие смысла, минимального или же максимального значение параметра оптимизации y, нужно выполнить серию опытов, в любом из которых задается смысл независящей переменной x и сохраняется значение от зависящей переменной y.

     Итогом серии из n опытов считается большое количество пар чисел (, i=1,…n). Вслед за тем на базе приобретенной информации выбирают вид функции f и делается попытка выбрать значения в границах собственных пределов таким образом, дабы гарантировать хорошую точность описания опытных данных с поддержкой функции f.

     Нередко применяемая на практике мера свойства описания опытных данных ориентируется способом минимальных квадратов. Разница между экспериментальным значением и теоретическим значением y= f(x) демонстрирует, как буквально подобранная модель обрисовывает имеющиеся у нас данные.

      Следственно, задачу, описывающую данные, возможно рассмотреть как задачу оптимизации, в которой необходимо отыскать смысл характеристик, минимальных (максимальных) функций y.

      Указанные выдающие качества определяют высшую эффективность использования методов оптимизации в всевозможных процессах обработки металлов, в частности, для оптимизации геометрических характеристик режущего инструмента и режимов резания. Это особенно актуально при разработке новых технологических процессов при обработке труднообрабатываемых материалов, характеризующихся невысокой стойкостью режущего инструмента и свойства обработанных плоскостей [1].

      Наши данные показали, собственно, что в качестве параметра оптимизации имеют все шансы быть приняты надлежащие: стойкость инструмента; силы резания; степень автоколебаний технологический системы, включающей: станок–приспособление–инструмент–деталь (СПИД).

     На примере использующих моментов при данном имеют все шансы рассматриваться физические и механические качества обрабатываемых материалов и режущего инструмента; геометрические характеристики инструмента; режимы резания и др.

     В данном случае, при разработке технологической операции обработки режущим инвентарем имеет возможность быть представлена грядущая задача оптимизации: при известных материалах инструмента и заготовки найти такие значения геометрических характеристик инструмента и элементов режима резания (скорость -v, подача -s), в данной ситуации получается наибольшее значение стойкости инструмента.

     Важно отметить, что предоставленная стойкость инструмента обязана быть схожей при срезании толстой и узкой стружки, при обработке жесткого и мягкого материала, при обработке смазочно-охлаждающей жидкостью или же без нее. В расчетах по определению режима резания она является величиной знакомой или данной, и задача объединяется к вычислению подобной скорости резания, при которой инструмент  приобрел данную стойкость.

     Изучаю данную задачу, важно узнать степень влияния на скорость резания всех моментов, влияющих на стойкости инструмента. К количеству данных моментов, до этого всего, относятся физические и механические свойства обрабатываемого материала, толщины и ширины среза, геометрия инструмента и обстоятельства его работы.

     Таким образом, можно сделать вывод на данных опытах, что стойкость инструмента, один из ведущих параметров оптимизации, нежелательно применить в оптимизационных задачах. Тогда задача оптимизации имеет возможность быть сформулирована совсем другим образом: отыскать эти смысла составляющих геометрии инструмента (при неизменных v и s), при которых достигается наименьшее значение сил резания или меньшее смысл значения пульсации системы СПИД[2].

     Методы исследования. На практике задачи оптимизации принимают решение с внедрением полиномиальных моделей. Главная мысль заключается в применении аппроксимирующего полинома для описания модели. Важными критериями действенной реализации такового расклада можно считать унимодальность и непрерывность исследуемой зависимости.

     Из теоремы Вейерштрассе об аппроксимации, в случае если функция непрерывна в некотором интервале, то ее с всякой степенью точности возможно аппроксимировать полиномом более высокого порядка. Значит, в случае если функция унимодальна, и отыскан полином, который довольно буквально ее аппроксимирует, то координату точки оптимума функции возможно расценить методом вычисления координаты точки оптимума полинома.

     Качество оценок координаты точки оптимума, приобретенных с поддержкой аппроксимирующего полинома возможно увеличить или внедрением полинома более высокого порядка или уменьшением интервала аппроксимации. При этом второй метод больше предпочтителен, потому что построение аппроксимирующего полинома третьей и выше степени достаточно непросто[3].

     Сокращение интервала в заданных критериях, когда производится предположение об унимодальности функции, особенной трудности не дает. Все это имеет отношение к  функции одной переменной. В инженерных задачах мы нередко имеем дело с функциями небольшого количества переменных.

     Обсуждение результатов. Данный эксперимент хорошо доказывает, что задачи оптимизации технологических процессов действительно принимают решения на основе способов планирования многофакторных (многопеременных) опытов (ПФЭ).

     По данным опыта необходимо построить функцию отклика в виде уравнения регрессии

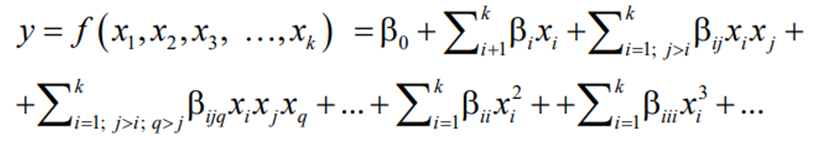
где β – коэффициенты, являющиеся производными вида ; i f x ¶ ¶ k – число факторов.

В данной модели (1) члены 2 3 , , x x x i i i и коэффициенты при них называют ключевыми эффектами, другие – эффектами взаимодействий. Для поиска коэффициентов уравнения регрессии применяется способ минимальных квадратов.

     Проделанный анализ доказал, что в всевозможных задачах изучения технологических процессов обработки металлов нередко применяется способ планирования опытов экспериментов по схеме, где 2 – число уровней варьирования факторов, n – количество независимых (факторов). Использование планов с n>2 достаточно увеличивает точность приобретенных результатов.

     В наглядности примера действительность применения методов планирования опытов при решении оптимизационных задач обработки металлов возможно привести итоги проделанных ранее экспериментов.

     В [4] доказали задачу оптимизации технологических процессов обработки резьб метчиками. Примером может послужить параметры оптимизации, который принимает вращающий момент при обработке внутренних плоскостей в заготовках из коррозионностойкой стали 12Х18Н10Т. Изучали воздействие на трех методов (υ- угол заборного конуса; α – задний угол заточки; γ передний угол). Для заключения данной задачи воспользовались ПФЭ плана 4х3х3. В результате было достигнуто увеличение стойкости инструмента более 45%, качества обработки и отнесены подходящие значения факторов, соответствующих наибольшей стойкости инструмента.

Вывод. Проделав данный эксперимент, указанный выше, и проанализировав поэтапно шаги наших действий, можно сказать о достаточно хорошей производительности и необходимости больше широкого использования научно-обоснованных способов оптимизации для анализа и обработки информации, в частности, для изучения и оптимизации всевозможных технологических процессов обработки металлов.