РАЗНОВИДНОСТЬ СПОСОБОВ РЕШЕНИЙ ОПТИМАЛЬНОСТИ

Решение оптимальности- это решение, которое по заданным стадиям является очень пригодным в данном положении. Смысл оптимального решения находится в определении выгодного варианта из всех имеющихся. Оптимальному решению дает хорошую характеристику его конкретность, т.е. решения, которые соответствуют заданным условиям.

 

Использование способов решений оптимальности в современном мире работает интенсивно. В данный момент это раздел математической науки, которая занимается подбором полезных способов организация хозяйства, производства на предприятиях.

 

Задачи оптимальности разделяются по нескольким элементам:

1.По числу вариантов в вопросительной функции способы косвенного программирования делятся на одновариантные и нескольковариантные;

2.По удлинению направленного отрезка способы подразделяются на одноизмеряемые и многомерные;

3.По присутствию воспрещений способы косвенного программирования делятся на воспрещающиеся и без воспрещений.

 

Главными способами решений оптимальности выступают прямые и косвенные.

 

Прямое программирование- это способ модельной оптимизации, в котором вопросительные функции и воспрещения строго прямые.

 

Приведем пример прямого программирования:

 

   

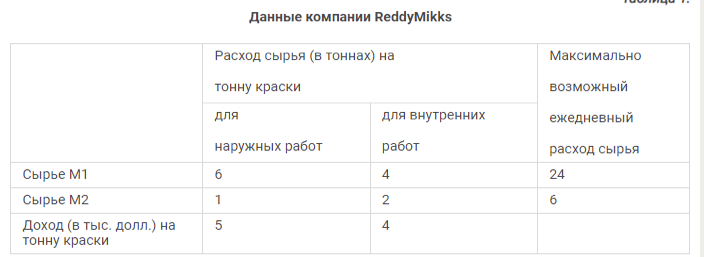
В задаче следует найти количество каждодневного производства краски для уличной и внутренней деятельности. Зададим эти количества как непостоянные модели:

 

У₁- каждодневное количество создания краски для уличных работ;

 

У₂- каждодневное количество создания краски для внутренних работ.

 

Анализирую данные переменные, построим вопросительную функцию:

 

H=5у₁+4у₂, H(имеет размерность в тысячах долларов)

 

Следуя с целями фирмы находим задачу: максимизировать H=5у₁+4у₂.

 

Далее запишем воспрещения на сырьевые продукты:

 

( Используемое_ количество)      ( Максимально_ допустимый)

( продукт_ для_ производства) ≤ ( каждодневный                     )

(двух_ типов_ краски              )    ( расход_ продукта                )

 

На основе таблицы получаем:

        

        Употребляемое количество сырья: K₁=6у₁+4у₂(к)

        Употребляемое количество сырья: К₂=1у₁+2у₂(к)

 

Так как каждодневный расход сырье имеет лимит 24 и 6 тонн, зададим       следующие ограничения:

       

      6у₁+4у₂≤24(сырье К₁)

      1у₁+2у₂≤6(сырье К₂)

 

Завершающим этапом данной задачи будет: максимизировать H=5у₁+4у₂ при следующих условиях:

 

      6у₁+4у₂<24

      1у₁+2у₂<6

      -у₁+у₂≤1

       у₂≤2

       у₁≥0, у₂≥0

 

Любое решение, которое соответствует условиям модели будет подходящим.

 

Отсюда следует, что данный вопрос имеет множество решений.

 

Косвенное программирование- это часть программирования, которая рассматривает методы решения экстремальных вопросов с косвенной вопросительной функцией.

 

Способы решения задач косвенного программирования:

   1.способ линейного поиска;

   2.способ градиентов первого порядка;

   3.способ градиентов второго порядка.

 

Смешанное программирование- это способ решения сложных задач путем разложения их на более простые задачи.

 

Заключение:

Способы оптимализации применяются в любой деятельности современного человека. А также занимают важное место в теории принятия решений.       Используя способы оптимальных решений, многие математические и экономические задачи можно решать легче. Так как главной задачей любой фирмы является хорошо максимизировать доход и сократить растраты на сбыт товаров.