РАСЧЕТ МАГНИТНЫХ ПРОВОДИМОСТЕЙ МАШИН С ПОСТОЯННЫМИ МАГНИТАМИ

Существующие магнитные цепи можно разбить на два основных типа по характеру образования и распределения магнитного потока в магнитопроводе.

1. Магнитные цепи, поток рассеяния которых мал и при определении параметров не учитывается;
2. Магнитные цепи, поток рассеяния которых необходимо учитывать.

Если через равномерную распределенную обмотку, расположенную на ферромагнитном тороиде (рис. 1) пропустить ток, то в кольце тороида образуется только основной поток, а поток рассеяния вследствие симметрии будет отсутствовать. Большинство магнитных цепей выполняют несимметричными, магнитопровод при этом может быть замкнут или иметь воздушный зазор. В таких цепях образуется магнитный поток рассеяния. Величина этого потока будет определяться размером воздушного зазора, конфигурацией магнитной цепи, степенью насыщения стали, наличием электромагнитных экранов (короткозамкнутых витков) и другими факторами. Степень учета поля рассеяния зависит в каждом отдельном случае от требований, предъявляемых к расчету. Магнитным потоком рассеяния можно пренебречь только при условии, что магнитопровод замкнут или воздушный зазор сравнительно мал, а магнитная цепь не насыщена.

Рисунок 1 – Магнитная цепь с одним рабочим потоком

Несимметричные магнитные цепи с переменной удельной проводимостью рассеяния наиболее характерны для синхронных машин с аксиальным потоком, которые приводят к сложному потокораспределению в магнитопроводе. Расчет проводимостей таких цепей должен основываться на картине поля [1].

Если мы рассмотрим магнитную цепь аксиальной синхронной машины с постоянными магнитами (рис. 2), то мы может отметить, что постоянный магнит работает совместно с внешней магнитной цепью, содержащей ферромагнитный сердечник с обмоткой, отделенной от магнита воздушными зазорами. Следовательно, расчет проводимостей потоков рассеяния воздушных промежутков оказывает большое влияние на точность расчета в целом. Поэтому при расчете проводимостей рассеяния по воздуху магнитная цепь разбивается на отдельные простейшие участки с учетом путей потоков рассеяния, т.е. общей картины поля [2, 3].

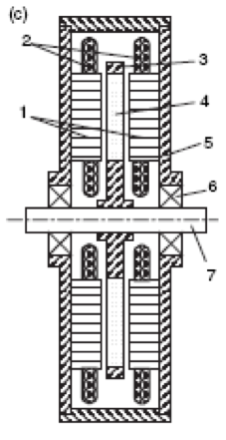
Рисунок 2 – Принципиальная схема аксиальной синхронной машины с постоянными магнитами

Представим магнитную цепь дисковой ВТСП электрической машины в виде схемы замещения (рис. 3), приведенную к простейшему виду.

Рисунок 3 – Схема замещения магнитной цепи дисковой ВТСП электрической машины

На схеме замещения представлены приведенные магнитные проводимости цепи. Причем характеристики магнитных проводимостей системы Gп, Gм можно принять за прямые только в том случае, если система не насыщена (рис. 3), а характеристики Gs всегда линейны. Метод нахождения напряженности внешнего размагничивающего поля Нв, приложенного к магниту, зависит от типа магнитной цепи и места нахождения внешней намагничивающей силы. Для определения результирующей проводимости цепи G₀ можно воспользоваться следующим выражением.

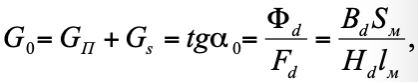
Так как приведенные проводимости полезного потока и потока рассеяния Gп и Gs находятся под одним и тем же магнитным напряжением концов магнита Fм0, то для них будет справедливо следующее отношение.

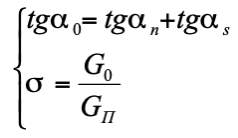
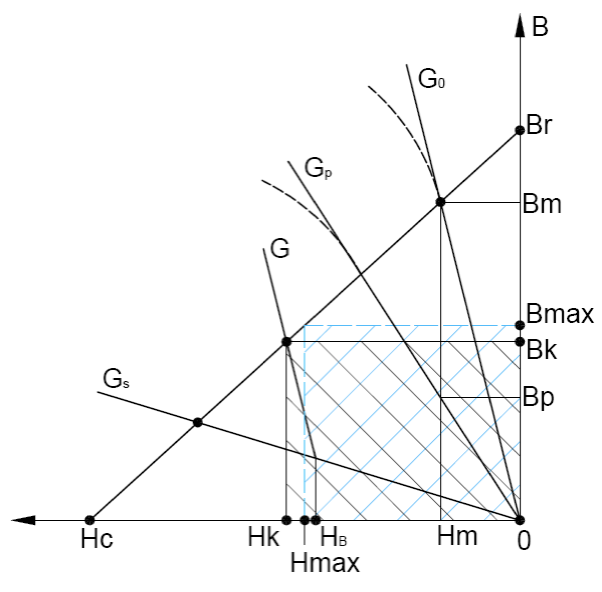
Рисунок 4 – Кривая размагничивания при влиянии реакции якоря ВТСП обмотки.

На основании рабочей диаграммы приведенной на рисунке 4 можно получить аналитическое выражение для подсчета величины полезного магнитного потока.

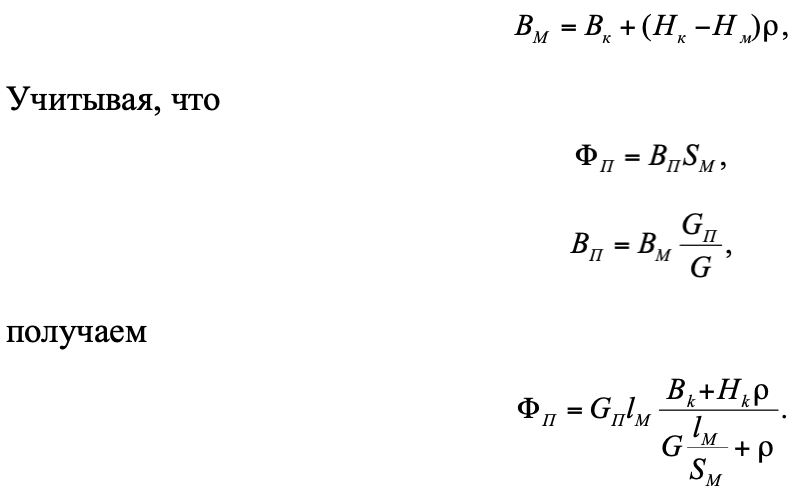
Как видно из выражения, полезный поток Φ_П возрастает с увеличением полезной проводимости, при этом для получения одного и того же потока при большем значении проводимости потребуется меньший объем магнита.

Для ВТСП электрических машин с постоянными магнитами расчет проводимостей воздушных промежутков имеет огромное значение, особенно, это сказывается на магнитных полях направленных перпендикулярно ВТСП ленте, которые резко ухудшают параметры ленты, а это в свою очередь скажется на рабочих параметрах электрической машины.

Непосредственное определение результирующей магнитной проводимости рассеяния по воздуху в цепях с постоянными магнитами возможно только в простейших частных случаях, когда магнит имеет простую форму. Основным допущением при расчете проводимости является предположение о ненасыщенности стальных участков магнитной цепи, поверхности которых являются эквипотенциальными.

Из схемы замещения может быть получена система уравнений.

b_M является точкой отхода прямой возврата, которая определяет величину полезной магнитной индукции в воздушном зазоре [4].

Можно выделить 2 зоны, для которых расчет проводимостей рассеяния можно свести к следующему виду.

Для области, обозначенной на рис. 5 цифрой 1 можно записать уравнение вида:

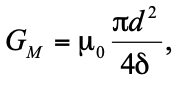
При условии, что отношение длины воздушного зазора и диаметра полюса исследуемой машины меньше 0,2 единиц, то определение проводимости сводится к следующему.

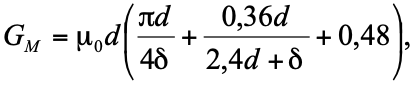
где d – диаметр магнита, δ – длина воздушного зазора.

Для области, обозначенной на рисунке 5 цифрой 2 магнитная проводимость рассеяния может быть определена как проводимость между двумя плоскими параллельными поверхностями, лежащими в одной плоскости.

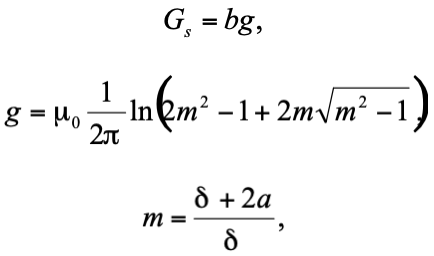
где b – диаметр полюса, а – диаметр полюса, g – удельная магнитная проводимость.

Рассмотренная выше магнитная цепь аксиальной синхронной машины является открытой, т.к. постоянный магнит работает без полюсных наконечников. В этом случае величина проводимости рассеяния может определить начальную точку прямой возврата на рабочей диаграмме магнита и, следовательно, электромагнитные характеристики машины. От точности расчета магнитных проводимостей постоянного магнита зависит точность всего электромагнитного расчета машины. При расчете проводимостей необходимо учитывать следующие особенности:

1. Намагничиваюшая сила по длине постоянного магнита является распределенной;
2. Поверхности магнита не являются эквипотенциальными;
3. Поле по длине магнита и по ширине не остается постоянным;
4. Различные точки магнита имеют различное состояние.

В связи с выше перечисленным для расчета проводимостей используют понятие приведенной проводимости рассеяния, которая представляет собой проводимость, эквивалентную по величине суммарному потоку рассеяния магнита, но приложены к концам магнита, т.е. соответствуют полной намагничивающей силе магнита.

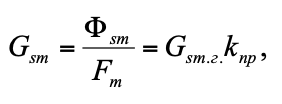
где G_sm.г. – геометрическая величина проводимости рассеяния магнита, k_пр – коэффициент приведения.

Величина коэффициента приведения зависит от характера изменения магнитного напряжения и от изменения проводимостей рассеяния по длине магнита. При расчете проводимостей (рис. 6) с резко различными удельными проводимостями рассеяния величину удельной проводимости рассеяния можно представить:

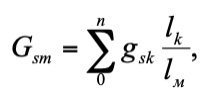
где l_k – расстояние между серединами к-той пары участков магнита.