Реализация и исследование метода декомпозиции для решения комплексной задачи геометрического покрытия и раскроя

Задачи оптимального покрытия и раскроя возникают во многих практических задачах – планировании технологических операций с использованием токарных и металлорежущих станков, компоновки печатных плат, экономическое планирование отделочных работ и др. Целью таких задач является размещение некоторого конечного множества объектов с заданными характеристиками в ограниченном ресурсе таким образом, чтобы некоторая целевая функция «качества» принимала максимальное значение, либо, наоборот, минимизировалась заданная «штрафная» функция.

Комплексная задача покрытия и раскроя заключается в совместном решении задачи определения покрытия или замещения заданной̆ области пространства некоторыми «элементами» с последующим их размещением на листах ресурса, из которого они могут быть изготовлены. Методы решения задачи покрытия, допускающие наличие перекрытий между элементами покрытия и различные формы элементов покрытия, описаны в работе [1].

В двумерной постановке данной задачи требуется осуществить покрытие прямоугольной области с запретными областями, каждая из которых может быть описана как объединение конечного количества прямоугольных областей, непересекающимися прямоугольными элементами. Полученное покрытие требуется разместить на листах ресурса или на полубесконечной ленте таким образом, чтобы минимизировать расход материала. Обе составляющие данной проблемы представляют собой сложные математические задачи, решению которых посвящено множество научных публикаций начиная с классической книги Канторовича [2]

В данной работе рассмотрен подход к решению комплексной задачи геометрического покрытия и раскроя многосвязного ортогонального полигона. Рассмотрена версия метода матричной декомпозиции покрываемой области, представленный в работах [3, 4], проведено его теоретическое исследование и предложена модификация метода с использованием метаэвристического метода оптимизации.

Важный частный случай двумерных задач покрытия/раскроя будет получен, если элементы покрытия представляют собой прямоугольные элементы, а область покрытия – прямоугольную область, в которой вырезаны внутренние области с прямоугольными границами (рис. 1-3, [3]). Такую область покрытия будем называть многосвязным ортогональным полигоном (МОП), вырезанные в нём области будем называть запретными зонами, а задачу покрытия такой многосвязной области – задачей ортогонального покрытия МОП. С задачей покрытия также сопряжена задача ортогонального раскроя, заключающаяся в поиске оптимального расположения элементов покрытия на ресурсе – прямоугольных листах материала с известными геометрическими размерами.

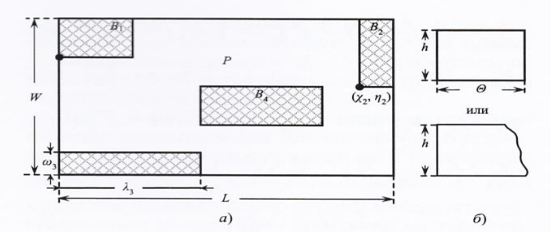
Рисунок 1. Иллюстрация постановки комплексной задачи: а) МОП P с запретными областями Bν; б) размеры ресурса

 

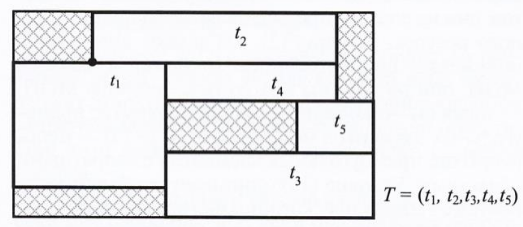
Рисунок 2 — План покрытия МОП P множеством покрывающих прямоугольников T

 

 

Каждый элемент покрытия может быть охарактеризован вектором значений (x,y,w,h), где (x,y) – координаты нижнего левого угла элемента покрытия в системе координат покрываемой области, w, h – его геометрические размеры.

Естественная характеристика качества для решения задачи покрытия МОП может быть получена из соображения, что количество стыков между элементами покрытия должно быть минимальным. Формально можно ввести следующую числовую характеристику покрытия T :

(1)

требующую, чтобы совокупный периметр покрытия был как можно меньше. Это отвечает эмпирическому представлению о том, что оптимальное покрытие должно состоять из как можно меньшего числа элементов.

С задачей покрытия связана задача раскроя, в которой для заданного множества T требуется найти допустимое размещение элементов покрытия на ресурсе. Характеристикой качества решения можно считать количество отхода материала:

                                                           (2)

где  w_max, h_max - размер листа ресурса, |T | – количество листов ресурса, необходимых для изготовления всех элементов покрытия.

Совместное рассмотрение задач покрытия и раскроя МОП приводит к необходимости многокритериальной оптимизации. В качестве критерия может быть взята вектор-функция

                                                                    (3)

где  F_cov(T)  – целевая функция покрытия; F⁽¹⁾_cut(T)  - целевая функция раскроя.

В современной вычислительной практике, с учётом сложности и разнообразия постановок задачи оптимального покрытия-раскроя, широкое применения нашли эвристические и метаэвристические методы численной оптимизации.

Для оценки качества работы алгоритма планирования покрытия и раскроя можно также использовать безразмерные характеристики, не чувствительные к изменению абсолютных размеров МОП и ресурса. В качестве такой характеристики для задачи покрытия будем рассматривать коэффициент покрытия:

                                                                             (4)

где S_pec - суммарная площадь использованного ресурса, P_pec и PT – суммарные периметры ресурса и элементов покрытия соответственно.  Безразмерной характеристикой качества раскроя будем считать коэффициент раскроя, определяемый формулой:

                                                                   (5)

Введение в рассмотрение этих характеристик позволяет оценивать качество работы алгоритмов решения поставленной задачи независимо от абсолютных размеров ресурса, покрываемой области и запретных зон.

Одним из эвристических методов, который рассмотрен в рамках данной работы, является метод матричной декомпозиции [3, 4].

Результатом работы алгоритма матричной декомпозиции будет матрица A, соответствующая ячейкам дискредитирующей сетки и указывающая на их принадлежность запретной области или покрываемой области, и матрица G, соответствующая узлам сетки и хранящая их координаты. Также алгоритм возвращает в качестве результата размер матрицы A.  Пример сеточного разбиения МОП показан на рисунке:

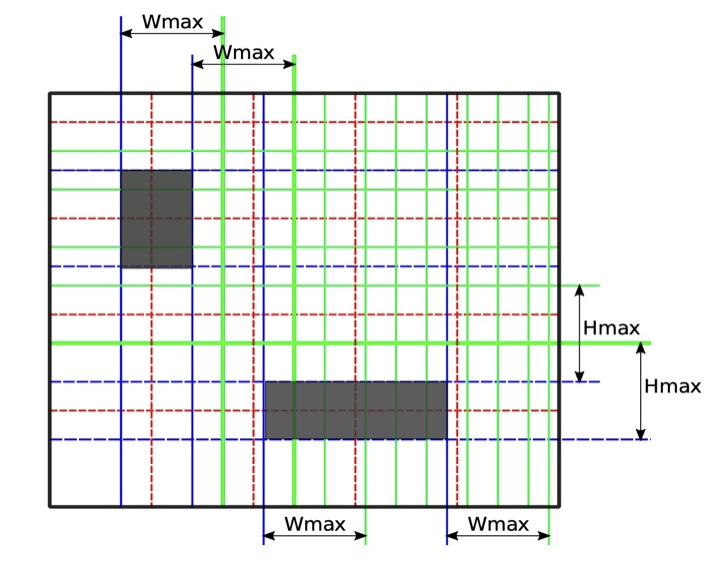
Рисунок 3 — Пример разбиения МОП на отдельные ячейки

Красным цветом обозначены границы, обусловленные размером ресурса wmax, hmax (или, в общем случае, максимально допустимым размером элемента дискретизированной области). Синим цветом обозначены границы элементов, соответствующие положению вертикальных и горизонтальных граней элементов запретных областей. Зеленым обозначены вспомогательные линии разбиения. Их назначение в том, чтобы обеспечить возможность размещения элемента покрытия максимально возможного размера при том, что одна из его граней лежит на линии реза.

Применение алгоритма матричной декомпозиции позволяет во многих случаях получить приемлемое решение. При этом он очень экономен с точки зрения затрат вычислительных ресурсов. Эвристическое правило, задающего стратегию поиска покрытия, заключается в стремлении на каждом этапе закрыть как можно большую часть незакрытой области так, чтобы уместиться в ресурс.

Модификация метода матричной декомпозиции. Методы DPSO.

С целью улучшения результатов алгоритма матричной декомпозиции можно предложить два алгоритма. Для инициализации алгоритма требуется построить набор из K значений, принадлежащих области определения целевой функции. K – параметр метода, называемый размером роя. Работа алгоритма на определенном этапе решения проиллюстрирована на рисунке:

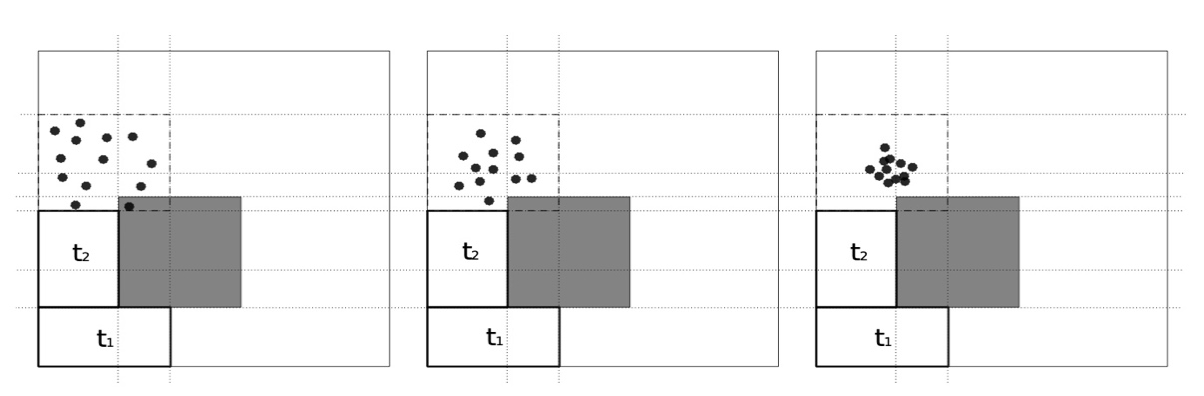
Рисунок 4 — Иллюстрация работы алгоритма PSO

Второй алгоритм (приближенный) представляет собой упрощенную версию первого, в котором на каждой итерации задача минимизации решается приближенно с использованием обычного метода матричной декомпозиции. Это существенно сокращает вычислительные затраты, хотя и приводит к ухудшению полученного решения.

Для оптимизации целевой функции в таком случае используем алгоритм дискретного метода роя частиц (DPSO), описанный в [5]. Модифицированная целевая функция, оптимизируемая в данном алгоритме, имеет вид:

                                                                   (6)

где S – числовой штрафной коэффициент (наличие дополнительного штрафного слагаемого приводит к смещению сформировавшихся на ранних этапах кластеров частиц в сторону заданных дискретных значений.

Данный алгоритм исследован в работах [5] и показал хорошие результаты в задачах нелинейной дискретной оптимизации.

Отметим, что в случае достаточно простой формы покрываемой области и запретных зон достаточно грубой сетки – вплоть до той, что используется в алгоритме матричной декомпозиции. В этом случае в процессе выполнения шага алгоритма целевая функция будет вычислена во всех допустимых на итерации узлах сетки и, следовательно, задача минимизации может быть решена точно без привлечения PSO. В качестве критерия сходимости использовано предельное среднеквадратичное отклонение σ частиц от центра роя.

                                                                                      (7)

                                                                           (8)

где K – размер роя, xi – положение i-й частицы в пространстве параметров, σmin – параметр метода, определяющий минимально допустимую величину разброса частиц роя.

Многоуровневый DPSO-алгоритм

Качество получаемого решения можно дополнительно улучшить, если в сформулированном алгоритме DPSO допустить применение не алгоритма матричной декомпозиции, а другого алгоритма, дающего, возможно, лучшее решение. В качестве такого вложенного алгоритма может выступать сам алгоритм DPSO. Однако, как отмечалось ранее, это приведет к экспоненциальному росту сложности, поскольку потребуется решать рекуррентную последовательность оптимизационных задач. Для избегания этого ограничим максимальный уровень вложенности в алгоритме. Алгоритмом DPSO уровня 0 будем считать алгоритм матричной декомпозиции. Легко видеть, что описанный алгоритм DPSO является DPSO-алгоритмом уровня 1. В работе реализован алгоритм DPSO с произвольным уровнем вложенности. В приложении с графическим интерфейсом доступны методы DPSO-L1 и DPSO-L2 для решения задачи оптимального покрытия МОП. Использование алгоритмов с большим уровнем вложенности не рекомендуется по причине больших сопутствующих вычислительных затрат.

Жадный алгоритм раскроя

Задача алгоритма раскроя заключается в размещении элементов построенного покрытия целевой области на листах ресурса. В данной работе использовался жадный алгоритм размещения, в котором используется алгоритм матричной декомпозиции для решения подзадачи.

Алгоритм реализует жадную стратегию, поскольку на каждой итерации производится попытка разместить как можно больший по площади элемент покрытия. Если это удается, то далее производится попытка разместить на том же листе другие элементы покрытия, причем также в порядке убывания их площади.

Рассмотренные алгоритмы реализованы в специализированном программном обеспечении, которое позволяет задавать конфигурацию целевой области, параметров покрытия и проводить решение комплексной задачи покрытия и раскроя. Пример результата одного из экспериментов, в котором оценивался коэффициент покрытия kcov для указанных алгоритмов, показан на рисунке.

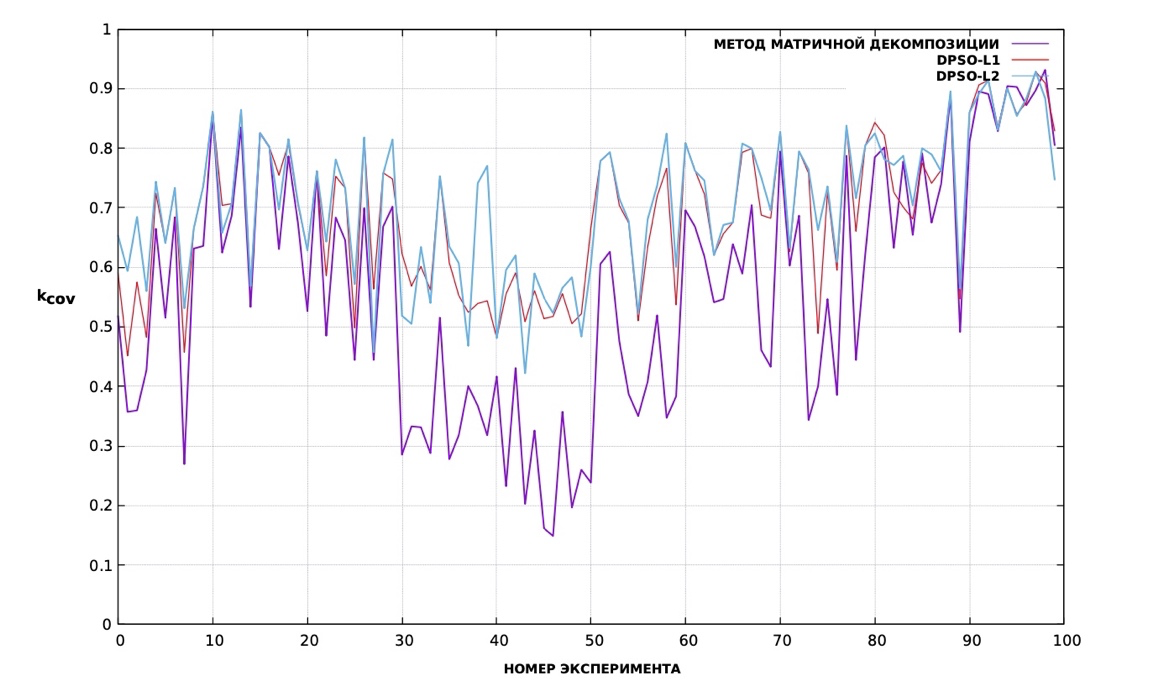
Рисунок 5 — Экспериментальное исследование алгоритмов покрытия-раскроя

 

На данном графике видно, что алгоритм уровня 2 показывает стабильно лучшие в плане значения коэффициента покрытия результаты по сравнению с алгоритмом уровня 1 и алгоритмом матричной декомпозиции. Однако улучшение по сравнению с результатом, получаемым алгоритмом первого уровня, существенно уступает улучшению, которое дает алгоритм первого уровня по сравнению с алгоритмом матричной декомпозиции.

Был проведен ряд независимых вычислительных экспериментов. Результат одного из расчетов приведен в таблице 1.

Таблица 1.

Вычислительный эксперимент

Алгоритм	Fcov, %	Fcut, %	Время работы
Матричная декомпозиция	0	0	1
DPSO-1 :	51.3	0.85	158
DPSO-2 :	63.37	-1.55	73503
DPSO-1 : kcut	-19.15	20.44	49367
DPSO-1 : kcov	49.69	2.75	1909

 

Из приведенной таблицы видно, что алгоритм DPSO с оптимизацией по критерию качества покрытия позволяет существенно улучшить качество покрытия. При этом значение коэффициента раскроя, как правило, уменьшается, однако ухудшение не превышает 3%. В случае, когда оптимизация проводится по критерию качества раскроя, качество покрытия существенно ухудшается. Двухуровневая оптимизация позволяет достичь дополнительного улучшения показателей качества, однако это требуем достаточно существенного (на порядок) увеличения вычислительных затрат. Дополнительно следует отметить, что предложенные модификации метода матричной декомпозиции естественным образом параллелятся, что также увеличивает их область потенциальной применимости.