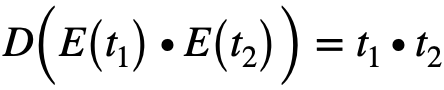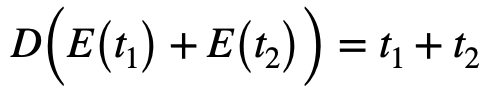ПОЛНОСТЬЮ ГОМОМОРФНОЕ ШИФРОВАНИЕ

Гомоморфное шифрование – это форма шифрования, которая позволяет производить определенные математические действия с зашифрованной информацией и получать соответствующий результат без ее предварительного дешифрования. В отличие от стандартных систем, в схеме гомоморфного шифрования используется четыре процедуры, включая операцию выполнения вычислений над шифрованным текстом [3]. Это дает возможность работать с зашифрованными данными пользователя, сохраняя их безопасность и конфиденциальность.

Пусть Е – функция шифрования, D – функция расширования, t₁ и t₂ — открытые тексты. Криптосистема является гомоморфной относительно операции умножения, если

и гомоморфной относительно операции сложения, если

Система шифрования является полностью гомоморфной (Fully Homomorfic encryption, FHE), если она гомоморфна относительно операций сложения и умножения, т.е. выполняются равенства (1) и (2). Данный вид криптосистем подходит для облачных сервисов, которым необходим больший функционал. Полностью гомоморфное шифрование может иметь весомое практическое значение в аутсорсинге закрытых вычислений [2]. FHE позволяет проводить больше вычислений над зашифрованными данными, поддерживая операции с возможностью сложения и умножения. Но и у FHE есть свои ограничения на поддержку широкого спектра операций или функций. Это связано с тем, что две функции могут послужить отмене друг друга, делая зашифровку бессмысленной.

Примером полностью гомоморфной криптосистемы может послужить схема Джентри. Рассмотрим систему шифрования в кольце двоичных чисел.

Выбирается произвольное нечетное число p = 2k + 1, где p – секретный ключ. Допустим, необходимо зашифровать бит 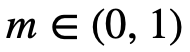. Для этого сгенерируем число 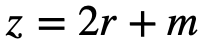, где r – произвольное число. Следовательно, .

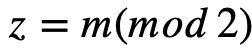Шифрование заключается в том, что любому числу m ставится в соответствие число 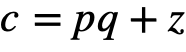, где q – произвольное целое число. Это значит, что 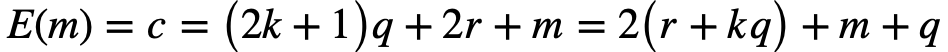. Именно число c подвергается вычислениям.

Затем следует расшифрование. Пусть известны числа c и p. Проведем расшифрование с помощью секретного ключа p:

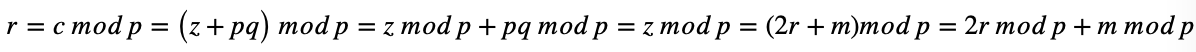
И тогда зашифрованный бит:

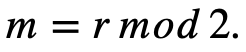
Шифрование является гомоморфным относительно операции сложения и умножения, т.е. полностью гомоморфным.

Недостатком данной схемы является ошибка r – так называемый шум, накапливающийся при проведении расчётов над текстом и препятствующий его расшифровке. После превышения ошибкой числа p расшифрование становится невозможным. В качестве решения данной проблемы Джентри был предложен механизм самокоррекции шифрованных текстов, однако такой метод приводит к быстрому росту размера шифротекста и не является практичным. Необходимо ограничение количества операций над данными или усовершенствование алгоритмов вычисления.

На сегодняшний день активно проводятся исследования в области гомоморфного шифрования, нацеленные на контролирование точности и скорости вычислений в схемах. В открытом доступе находятся некоторые реализации полностью гомоморфных криптосистем новых поколений, например схема FHEW. С ее помощью было показано, что, обновляя зашифрованные тексты после каждой отдельной операции, можно сократить время самокоррекции шифротекстов до доли секунды. [1]