при составлении уравнений для определения угловых координат звеньев механизма аналитическим методом, почти всегда возникает необходимость ввести еще какие-то дополнительные условия. Но электронно-вычислительные машины для функции arctg из двух ответов, т.е. углов, относящихся к первой и третьей четвертям, в качестве ответа всегда дают угол, расположенный в первой четверти, хотя в действительности этот угол может находиться в третьей четверти. А из двух углов, относящихся ко второй и четвертой четвертям, ЭВМ всегда в качестве правильного ответа предлагает угол четвертой четверти. Точно так же для всех остальных тригонометрических функций не всегда можно получить действительное значение угла, а угол, который симметричен действительному углу относительно одной из осей или начала системы координат.
Чтобы выбрать правильное решение из двух вариантов, вводятся дополнительные условия. Рассмотрим такие условия на примере определения угловых координат коромысла и шатуна шарнирно-четырехзвенного механизма, которые даны в [1].
Из расчетной схемы, приведенной на рис. 1, получены уравнения для определения угловых координат φ3 и φ2 :
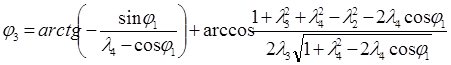
; (1)
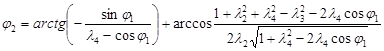
, (2)
где
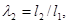
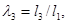
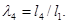
Дополнительное условие, о котором говорилось выше, в данном случае введено следующим образом [1]: если sgn(xD-xB)=1, то угловая координата базового вектора φв, т.е. первое слагаемое в уравнениях (1) и (2) остается неизменным:
.
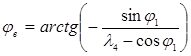
Если sgn(xD-xB)= -1, то
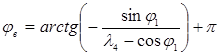
Введение этих условий при составлении программы расчета на ЭВМ не вызывает никаких затруднений, но сама запись уравнения с учетом приложенных условий неудобна. Чтобы исключить эти неудобства, необходимо ввести дополнительные условия в само уравнение [2].
Предлагаем для этого угловую координату φв базового вектора выразить через arсcos. Для этого используем расчетную схему, приведенную в [3] (рис. 2).
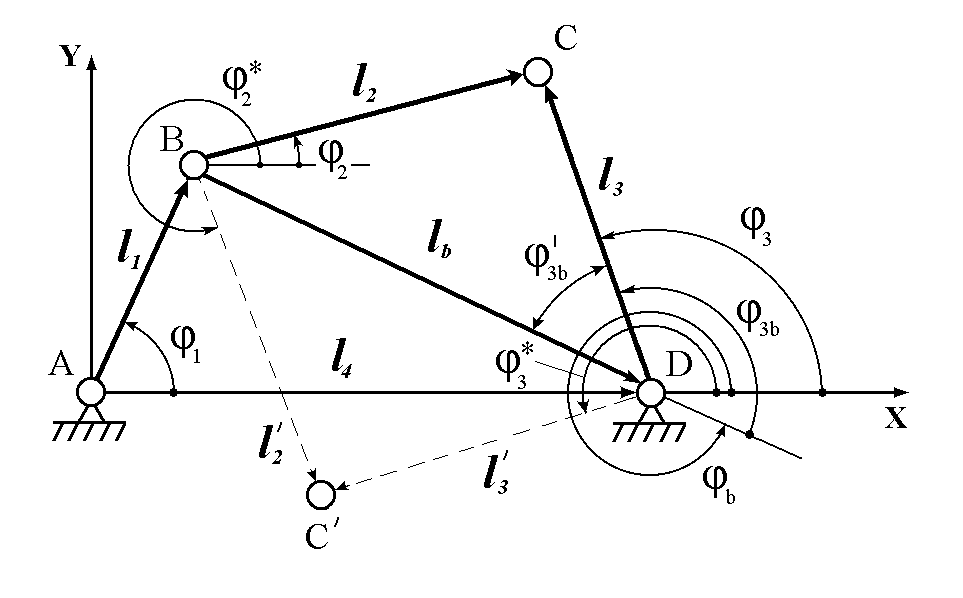
Рис. 2. Расчетная схема для определения угловых координат звеньев, в которой вектор i3 направлен от точки D к точке С.
Из треугольника АВD по теореме косинусов имеем:
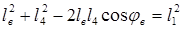
.
Отсюда, введя относительные размеры звеньев
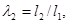
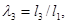
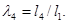
и
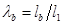
и учитывая, что
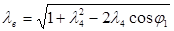
, получим:
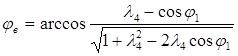
(3)
Уравнение (3) используется аналогично уравнению физического маятника , для стабилизации которого использован упругий элемент , что позволяет , при определенных силовых и геометрических параметрах механизма , получить положительный результат.
Данная методика анализа и способ обеспечения устойчивости данного механизма применительна и к механизму со сходящимися по ходу движения тягами.
Список литературы
- Артоболевский И.И. Теория механизмов и машин: [Учеб. для втузов]. – 4-е изд., перераб. и доп. – М.: Наука, 2009. – 639 с.: ил.; 22 см.
- Кореняко А.С. «Курсовое проектирование по теории механизмов и машин», Издательство «Вища школа», 2007 г. ? 326с.
- Решетов Д.Н. «Детали машин» учебник для вузов. Р47 Изд. 3-е М., «Машиностроение», 2008.
- Теория механизмов и машин. Терминология: Учеб. пособие / Н.И.Левитский, Ю.Я.Гуревич, В.Д.Плахтин и др.; Под ред. К.Ф.Фролова. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2007.– 80 с.
- Теория механизмов и механика машин: Учеб. для втузов / [К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – 2-е изд., перераб. и доп. – М.: Высш. школа, 2008. – 496 с.: ил.



