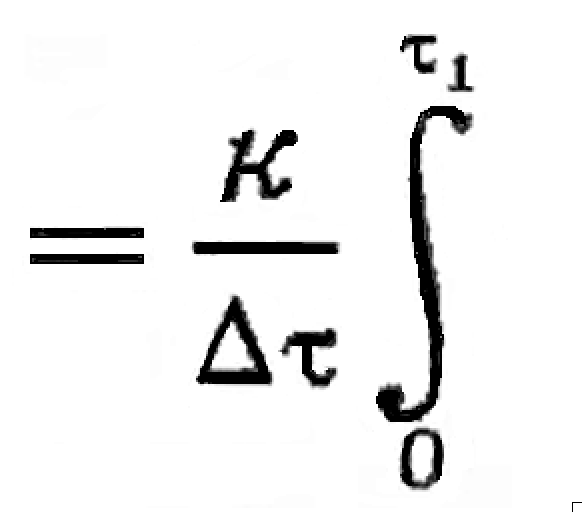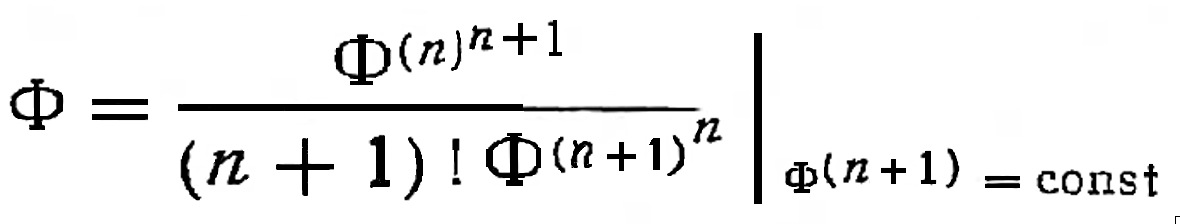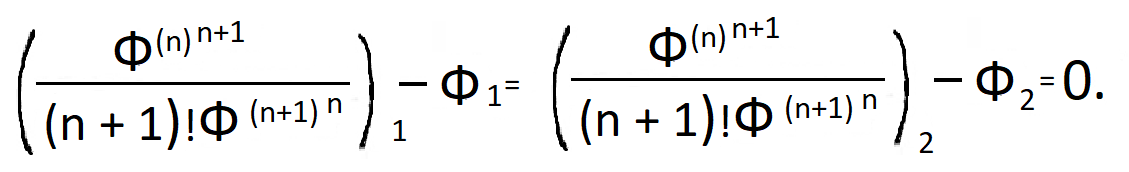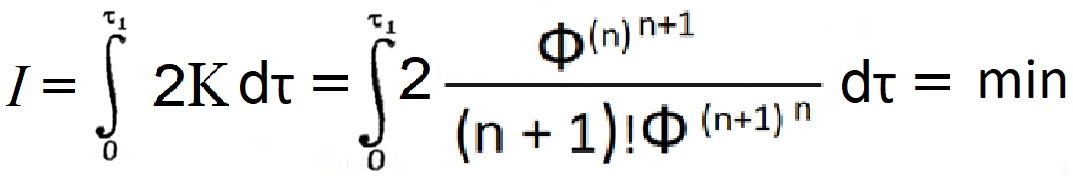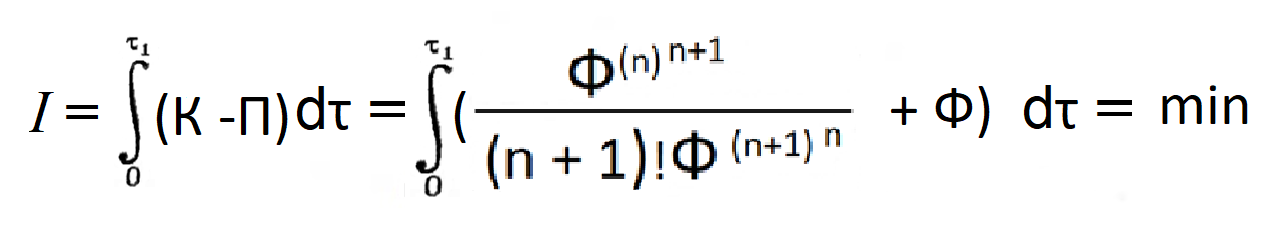ТЕРМОДИНАМИЧЕСКОЕ ВРЕМЯ УСТРАНЯЕТ КОЛЛАПС ВОЛНОВОЙ ФУНКЦИИ В УРАВНЕНИИ ШРЕДИНГЕРА

1. ВВЕДЕНИЕ

Физический смысл волновой функции Шредингера долгое время оставался предметом дискуссий и различных интерпретаций по мере развития квантовой механики.

В своей основе волновая функция (обычно обозначаемая как Ψ) представляет собой математическое описание состояния квантовой системы. Волновая функция содержит информацию о вероятностях нахождения частицы в разных точках пространства и о значениях физических параметров (импульс и энергия).  Численное значение Ψ является расчетной величиной вероятностной амплитуды, не измеримой непосредственно. Квадрат её модуля (|Ψ|2) даёт плотность вероятности нахождения частицы в определенной точке пространства.

До сих пор нет полного понимания списка свойств, которыми обладает (или должна обладать) волновая функция. Неясно, например, обладает ли волновая функция свойствами термодинамической функции состояния?

Здесь нет однозначного ответа.

• Аргумент «ЗА»: Волновая функция однозначно задает состояние системы и позволяет рассчитать любые наблюдаемые величины, подобно тому, как функции состояния определяют макроскопические свойства определенных термодинамических параметров (внутреннюю энергию, энтропию, энергию Гиббса и др.).
• Аргумент «ПРОТИВ»: Волновая функция описывает микросостояние (квантовые), а не термодинамические функции, которые представляют собой статистические усреднения по множеству микросостояний.

Однако не это различие является принципиальным. Важнее всего, что функция состояния не зависит от пути, по которому изучаемая система приведена в данное состояние. Функция состояния имеет математические свойства полного интеграла и полного дифференциала. Функции состояния взаимно связаны дифференциальными уравнениями.

 

В этом плане, волновая функция подчиняется только уравнению Шрёдингера, которое не дает информации о промежуточных состояниях частиц - пути и этапы квантовых изменений нам неизвестны. 

 

Развитие неравновесной термодинамики (или термодинамики спонтанных процессов) задержалось более, чем на 100 лет по простой причине: модели времени по Ньютону и Эйнштейну описывают время как нейтральный внешний параметр, не обладающий свойствами функции состояния и не оказывающий влияния на ход физического или химического процесса.

 

Анализ литературных данных показывает, что уравнение Шрёдингера дает прекрасные результаты при решении стационарных задач. Сбои наблюдаются при переходе к динамическим задачам. В частости, общеизвестен парадокс коллапса волновой функции в некоторый момент времени.

 

Цель данной работы – представить вниманию исследователей понятие «термодинамическое время», которое является оператором, основанным на авторской методологии научных открытий [1] (распространение Принципа Ферма на другие виды физического и химического движения). Данная модель времени, обладающая свойствами функции состояния, открывает путь к устранению коллапса волновой функции. При этом момент начала отсчета времени имеет причинно-следственную связь со всеми другими функциями состояния.

2. ЛИТЕРАТУРНЫЙ ОБЗОР

2.1. Волновая функция и модель времени

Волновая функция, Ψ(r, t), представляет собой математическое описание квантового состояния системы и эволюционирует во времени под воздействием гамильтониана, H, согласно уравнению Шрёдингера:

 

 

 

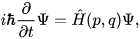
где ħ — приведенная постоянная Планка, H — гамильтониан, q — координаты, p — импульсы.

 

В этой формулировке время выступает как внешний параметр, индексирующий эволюцию волновой функции.

 

Модель времени в волновой функции тесно связана с вероятностной интерпретацией квантовой механики. Как было указано ранее, квадрат модуля волновой функции (|Ψ(r,t)|²) представляет собой плотность вероятности обнаружения частицы в точке r в момент времени t. Таким образом, время играет роль   нейтрального внешнего параметра, отмечающего изменения вероятности со временем.

 

В рамках квантовой теории поля время рассматривается более фундаментально, как часть пространства-времени, в котором и происходит эволюция квантовых полей [2]. Это приводит к концепции релятивистской квантовой механики, где время и пространство связаны между собой посредством преобразований Лоренца.

 

2.2. Эффективность волновой функции при решении стационарных и динамических задач

 

Уравнение Шрёдингера, демонстрирует высокую эффективность при решении стационарных задач, то есть задач, в которых гамильтониан системы не зависит явно от времени. В этих случаях, решение уравнения Шрёдингера сводится к нахождению собственных функций и собственных значений гамильтониана, определяющих стационарные состояния системы. Подход успешно применяется для описания атомных и молекулярных систем в основном и возбужденных состояниях (например, расчет энергетических уровней атома водорода).

 

В случае динамических задач, возникает ряд трудностей. В их числе некоторые физические ограничения, математическая сложность, трудность получения физически осмысленных решений. Однако наиболее непонятной трудностью в этом ряду является коллапс волновой функции.

 

Складывается впечатление, что большая часть этих трудностей порождена одной фундаментальной причиной, а именно – использованием модели времени, не обладающей свойствами функции состояния. Иными словами, отсчет времени не имеет причинно-следственной связи с функциями состояния. Шкала времени не определена.  Единственным известным квантовой системе моментом времени оказывается момент измерения. В отсутствие физически выделенной точки начала отсчёта коллапс неизбежен.

 

Между тем, модель термодинамического времени со свойствами функции состояния предложена еще в 1989 году [3], что позволило снять с повестки дня проблему неравновесности и перейти к построению термодинамики спонтанных процессов с перспективой развития инфо-термодинамики.

3. ТЕОРИЯ

3.1. Термодинамическая концепция времени

Прежде всего необходимо отметить, что концепция времени содержится в Общем начале термодинамики:

 

Неравновесная изолированная система с ограниченным сверху объемом имеет состояние устойчивого равновесия, в которое приходит за конечный отрезок времени.

 

Как следствие Общего начала и Принципа Ферма, можно сформулировать принцип:

 

Равновесное состояние термодинамической системы отделено от текущего неравновесного состояния кратчайшим отрезком времени, обладающим физико-математическими свойствами функции состояния, связанной дифференциальными уравнениями с другими функциями состояния исследуемой системы.

 

Исходя из данного принципа, термодинамическое время нельзя считать нейтральным внешним параметром - оно приобретает смысл активного физического фактора, вносящего свой вклад во все объективно измеряемые параметры. Отсюда, соответственно, следует существование времени-подобной функции состояния, которая получила название «термодинамическое время» [4].

 

Между термодинамикой и кинетикой существует фундаментальный разрыв понятий. Общее начало термодинамики противоречит постулату формальной кинетики о недостижимости равновесия за конечный отрезок времени. Мы отдаем предпочтение термодинамике, учитывая мнение А. Эйнштейна, что термодинамика изучает явления природы, тогда как другие физические науки изучают упрощенные модели явлений природы. Решённая в рамках термодинамического познания задача построения оператора времени, обладающего свойствами функции состояния [4], позволяет исследовать возможность использования новых термодинамических понятий применительно к задаче устранения коллапса волновой функции в уравнении Шрёдингера.

 

Как было сказано ранее, из приведенной выше формулировки Общего начала термодинамики следует существование времени-подобной функции τ, имеющей физический смысл кратчайшего отрезка времени, отделяющего данное неравновесное состояние от состояния равновесия. Будем считать функцию τ положительно определенной:

τ = ± (tравн − t), τ ≥ 0,

(1)

где τ — термодинамическое время (оператор времени, обладающий свойствами функции состояния).

 

t_равн — момент достижения равновесия по шкале лабораторного времени t.

 

Знак «±» определяется выбором направления отсчета лабораторного времени. Функция τ инвариантна по отношению к выбору начала и направления отсчета лабораторного времени. Отсчет лабораторного времени может производиться как в прямом, так и в обратном направлениях. Прямое направление соответствует направлению астрономического времени. В этом случае знак «-» можно опустить.

 

Самопроизвольный процесс идет в сторону установления равновесия с уменьшением величины τ (dτ<0). Иными словами, отсчет термодинамического времени производится в обратном направлении относительно хода астрономического времени и показывает величину отрезка времени, остающегося до перехода системы в равновесное состояние. Система, находящаяся в состоянии устойчивого равновесия, характеризуется минимальным значением τ = 0, при этом dτ/dt = 0.

 

Поскольку существование устойчивого равновесия постулировано Общим началом термодинамики, примем без доказательства условия устойчивого равновесия:

δτ= 0, δ2τ > 0

(2)

В стационарном состоянии τ = const.

 

В самопроизвольном процессе релаксации к равновесию функция τ характеризует степень отклонения системы от равновесия, является непрерывной, невозрастающей и, по крайней мере, кусочно-гладкой на множестве (t).

 

Функция τ является время-подобной, поскольку существенно отличается от свойств физического времени как координаты четырехмерного континуума пространства–времени. Например, при достижении равновесного состояния ход термодинамического времени вообще прекращается, а в дискретной неравновесной системе, состоящей из частиц различного состава и размеров, термодинамическое время отдельных частиц приобретает свойства статистически распределенной величины.

 

Самая главная особенность термодинамического времени τ заключается в том, что, в отличие от времени t, оно не является продуктом квантовой суперпозиции.  Величина τ не зависит ни от пути, по которому система была приведена в неравновесное состояние, ни от траектории, по которой внешние силы могут направить процесс в будущем, ни от выбора начала и направления отсчета лабораторного времени. В отличие от традиционно присутствующего в уравнениях механики и физики времени, термодинамическое время τ, обладает свойством квантовой идентичности.

 

Еще одной очень важной особенностью термодинамического времени как функции состояния является применимость к неравновесным системам с произвольной степенью неравновесности. Общность критерия направленности самопроизвольного процесса в форме dτ < 0 выше критерия dS > 0, поскольку энтропия как функция состояния не определена для состояний c произвольной степенью неравновесности. Добавим также, что термодинамическое время, в отличие от энтропии, обладает свойствами интенсивной величины.

 

3.2. Термодинамический вывод вариационного принципа в форме Гамильтона.

 

По Шрёдингеру [5], энтропия и негэнтропия образуются одновременно в результате диспропорционирования свободной энергии:

− Аmax = ΔΦ – TΔS,

(3)

где   А_max - максимальная работоспособность;

ΔΦ –- снижение потенциала неравновесного состояния в результате расхода энергии на создание негэнтропии;

 

TΔS –- расход энергии на создание энтропии.

 

Потенциал неравновесного состояния Φ и термодинамическое время τ из Общего начала термодинамики определены экстремально: как было сказано выше, система достигает равновесного состояния за кратчайшее время. Других независимых переменных, управляющих процессом развития системы, не имеется. Уравнение семейства энергетических траекторий спонтанного процесса можно получить решением дифференциального уравнения, в котором дифференциал потенциала неравновесного состояния принят тождественным дифференциалу от производной по термодинамическому времени (n)-го порядка этого же потенциала при условии, что производная порядка (n+1) есть величина постоянная, т.е. Φ⁽ⁿ⁺¹⁾ = const.   Следовательно, в равновесном состоянии все производные равны нулю, кроме постоянной Φ⁽ⁿ⁺¹⁾.

 

Решим дифференциальное уравнение

dΦ = dZ(Φ(n)),

(4)

используя известное соотношение для последовательных производных. После интегрирования получаем семейство разрешенных траекторий спонтанного процесса в виде степенных функций общего вида:

-ΔΦ = Φ(n+1) ∙ τn+1 / (n + 1)!,

(5)

где n = 1, 2, 3...– диссипативный порядок траектории, численное значение которого в каждом случае подлежит экспериментальному определению.

 

Уравнение (5) мы назвали уравнением развития.

 

Негэнтропия Шрёдингера представлена множителем Φ⁽ⁿ⁺¹⁾. Термодинамическое время τⁿ⁺¹ является интегрирующим множителем. В спонтанных процессах реализуются только те траектории, которые удовлетворяют уравнению (5).

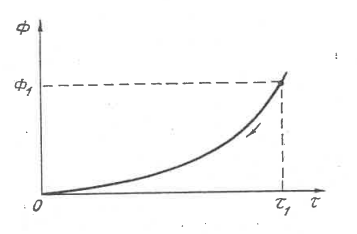
Рисунок 1. Схематическое изображение траектории самопроизвольного перехода изолированной системы из неравновесного состояния (Ф₁, τ ₁) в равновесное состояние (0, 0)

 

Величину изменения потенциала (—ΔФ) при релаксации системы к равновесию можно считать пропорциональной средней величине (2(—ΔФ)) за интервал термодинамического времени Δ τ = (τ₁ — 0):

 

— ΔФ

2(—ΔФ) dτ = min φ,

(6)

 

где φ – диссипация энергии, к – коэффициент пропорциональности.

 

Нет причин полагать к =1 или, иными словами, что среднее по интервалу значений функции — ΔФ должно быть равно среднему значению — ΔФ за интервал времени в диссипативном процессе. Но из предположения, что кроме Ф и τ нет других независимых переменных, характеризующих степень отклонения системы от состояния равновесия, следует к = const.

 

Уравнение (6) представимо в форме вариационного принципа:

 

I =

Фdτ = min

(7)

 

где -- ΔФ = Ф, так как Ф_равн = 0, и к/Δ τ = const, а, соответственно, не влияет на форму записи вариационного принципа.  Интеграл рассеяния в уравнении (7) имеет размерность действия, соответствует изохронной вариации:

 

δI = δ

ϕdτ = 0

(8)

 

и минимизирован на действительной траектории самопроизвольного   процесса. При этом подынтегральное выражение является полным дифференциалом. Очевидна аналогия между уравнением (7) и принципом наименьшего действия в механике. Имеется, однако, и принципиальное отличие: интеграл действия I является диссипативным по своей природе и был выведен из свойства инерциальности самопроизвольных процессов в смысле Власова [6], то есть совершенно независимо от принципа наименьшего действия в механике.

 

Уравнение (5) указывает на существование фундаментального запрета на произвольные формы энергетических траекторий в спонтанных процессах. Учитывая это, проанализируем уравнение (8), используя описанную в [7] собственную функцию неравновесной системы

 

(9)

 

где n= 2, 3... - диссипативный порядок процесса. Заметим также, что значения коэффициента к определяются соотношением к = (n+2) /2, так что к = const при n=const.

 

Если система самопроизвольно переходит из неравновесного состояния 1 в неравновесное состояние 2, то уравнение (9) можно переписать как

 

(10)

В таком виде оно представляется аналогом закона сохранения в механике

К +П = const, где К, П — кинетическая и потенциальная энергии.

 

Члены в уравнении (10), содержащие производные по термодинамическому времени, являются термодинамическими аналогами кинетической энергии. Величина Ф одновременно играет роль координаты в аналоге кинетической энергии и роль силовой функции (- П) = Ф.

 

Подстановка (10) в (9) приводит к уравнению

 

(11)

 

которое можно считать аналогом принципа наименьшего действия в механике в форме Мопертюи.

Принимая во внимание, что 2К = (К+П) + (К - П) = Е + (К - П), где Е = const, можем получить вариационный принцип в форме Гамильтона:

(12)

где концевые значения Ф иτ фиксированы и скорость на варьируемой траектории при n = const. такова, чтобы обеспечивалось выполнение требования минимального времени протекания процесса.

 

Проведенный анализ универсально справедлив для всех систем, в которых протекают процессы этого класса, независимо от степени их неравновесности. Множество переменных, характеризующих конкретную неравновесную систему, свернуто до функции одной переменной Ф (τ).  Имеющиеся экспериментальные данные, например [8], свидетельствуют, что такая простая модель является достаточно хорошей аппроксимацией многих реальных систем, начиная от механических, с трением, до гомогенных многостадийных химических реакций.

 

3.3. Примеры процессов различного диссипативного порядка:

 

Соотношение расходов энергии на создание негэнтропии и энтропии описывается простой формулой:

 

−ΔΦ / TΔS = n/2,

(13)

 

где n = 0, 1, 2, 3 …  –  диссипативный порядок спонтанного процесса.

 

Процесс диссипации энергии фотонов («красное смещение») характеризуется значением n = 0. Негэнтропия Шрёдингера не образуется.

 

Процессы для n = 1 обсуждаются С.Б. Алемановым в [9].

 

В случае химических реакций и механического движения без трения n = 2. Тогда, согласно (13), доля негэнтропийной компоненты в диссипативных потерях свободной энергии равна 50%.

 

Исследуем динамику сложных химических реакций. Системы с химическими превращениями относятся к классу систем с переменным количеством вещества в каждой из подсистем, образованных веществами, участвующими в реакции, поэтому следует пользоваться удельными значениями потенциала неравновесного состояния. В этом случае уравнение (5) приобретает вид:

 

φi = φi(n+1) ∙ τn+1 /(n+1)!,

(14)

 

где   φ_i = ∂Φ/∂m_i; m_i - число молей i-го вещества.

 

Протекание двухсторонней (обратимой) химической реакции ∑ν_i M_i  ↔️ ∑ν_j M_j удобно рассматривать с использованием методики "ящик Вант-Гоффа", которая обеспечивает переход к удельным величинам и вычислению химических потенциалов. Уравнение развития спонтанных процессов (5), в отличие от уравнений формальной кинетики, берет в рассмотрение только самопроизвольную, т. е. прямую реакцию. Наличие той или иной обратной реакции проявляется в уравнениях через посредство константы равновесия или заданных значений концентраций продуктов реакции. Свободная энергия реакции равна разности химических потенциалов продуктов и исходных реагентов:

 

─ Амакс = Δμ = ∑ νi RT(ln ai равн ─ ln ai),

(15)

 

где a_i — активности реагентов; ν_i — стехиометрические коэффициенты.

 

Подстановка (15) в (14) после небольших преобразований приводит к искомому уравнению энергетической траектории химической реакции:

 

∑ νi (ln ai РАВН ─ ln ai )  =  ∑ φi(n+1) ∙ τn+1 /αRT(n+1)!

(16)

 

Предполагается, что использование термодинамического времени уже учитывает неидеальность газов и растворов. Поэтому использование активностей вместо концентраций представляется избыточным. После подстановки вместо термодинамического времени τ текущего t, получаем:

 

[∑ νi (ln  Ci равн ─ ln Ci)] 1/n+1= const (tравн ─ t).			(17)
	i

Используя (17), можно строить график в координатах {[∑ ν_i (ln  C_{i равн} ─ ln C_i)], t}, чтобы определить момент достижения равновесия t _равн..       

 

3.4. Экспериментальное подтверждение конечного времени достижения химического равновесия

 

Для графической обработки были выбраны надежные данные [10] по кинетике сложных двухсторонних реакций трех типов с различными механизмами молекулярных преобразований:

 

№ 1.   Двусторонняя реакция первого порядка:

 

 

 

Компоненты (А) γ-оксимасляная кислота, (В) лактон (в водном растворе; С_{А нач} = 0,182 М, С_{А равн} = 0,0494 М; T = 298 К).).

 

№2.   Двусторонняя реакция второго порядка:

 

  

 

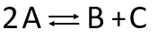
Компоненты реакции: HI (A); H₂ (B); I₂ (C).

 

С/C_o  - доля распавшегося HI.  С/С_{о нач} = 0; С/С_{о равн} = 0,2143.

 

№ 3. Двусторонняя последовательно-параллельная циклическая реакция типа:

 

 

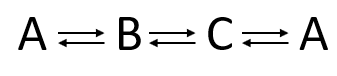
в ходе которой продукт C превращается в исходное вещество A.

 

Компоненты реакции:

 

CH₃CH₂CH ═ CHCOOH (A)

 

CH₃CH₂CH(OH)CH₂COOH (B)

 

CH₃CH═ CHCH₂COOH (C)

 

С_{А нач} = 100%; С/С_{А равн} = 41,3%

 

Во всех трех случаях химический процесс начинается с прямой реакции, в которой участвует только молекулы реагента А. Это позволяет использовать уравнение траектории в его простейшей форме:

 

(ln  С_{А равн} ─ ln C_А )^{1/ n+1}  =  const (t_равн ─ t)  

 

 

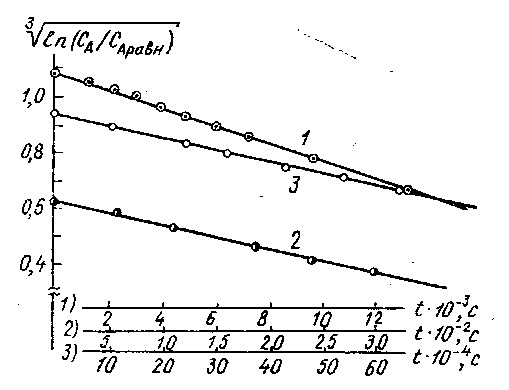
Рисунок 2.

 

Энергетические траектории реакций:

 

 

На Рис. 2 представлены графики вышеуказанных реакций в координатах

 

{( ln C_А ─ ln С_{А равн})^1/n+1 ,  t}. Численное значение n + 1 = 3 определено подбором.  Хорошо видно, что графики всех трех реакций имеют линейный характер. Это является подтверждением теоретических положений и уравнений термодинамики спонтанных процессов. Из графиков можно определить моменты достижения равновесия:

 

Реакция №	1	2	3
tравн сек	3,3∙104	9,9∙103	2,9∙106

 

Полученные результаты доказывают возможность использования уравнений термодинамики спонтанных процессов для описания динамики сложных химических реакций с различными механизмами химического превращения. Графики наглядно подтверждают конечное время достижения равновесия.

 

По сравнению с уравнениями формальной кинетики очень большим преимуществом является полное отсутствие эмпирических кинетических коэффициентов. Термодинамические функции (Φ и τ), могут выступать в роли макроскопических факторов, определяющих динамику химических превращений.

 

Закономерность на уровне открытия, определяющую ход исследованных химических реакций, можно сформулировать следующим образом:

 

Спонтанные химические реакции идут к состоянию равновесия по энергетическим траекториям кратчайшего времени, совместимым с условиями стехиометрии.

 

Полученные результаты приводят к выводу, что вероятностный механизм молекулярных столкновений жестко контролируется энергетическим факторами и оператором термодинамического времени со свойствами функции состояния.

4. ОБСУЖДЕНИЕ

Изложенные выше материалы свидетельствуют, что модели времени по Ньютону и Эйнштейну не дают объяснения многим явлениям физики, химии, особенно связанным с проблемами развития, усложнения и самоорганизации.

 

Традиционные уравнения механики и квантовой физики оказываются неработоспособными при решении новых задач. К числу возникающих трудностей относится и парадокс коллапса волновой функции Шрёдингера.

 

Путь к преодолению трудностей открывает уравнение (5), выведенное дедуктивным методом из физических и математических положений высочайшей общности, без использования гипотетических физико-молекулярных моделей и пригодное для описания любых самопроизвольных диссипативных процессов, независимо от их энергетической природы, вещественного состава, размеров, формы и внутренней структуры исследуемой системы.

 

Уравнение (5) не противоречит идее волновой функции. Фактически оно увеличивает число уравнений до количества неизвестных, к числу которых относится теперь и время, превратившееся из нейтрального внешнего параметра в активный физический фактор (термодинамическое время).

 

Результаты использования оператора термодинамического времени позволяют заключить, что для преодоления коллапса волновой функции также потребуется найти физически значимую точку начала отсчета времени. Используя (12), можно провести обратную аналогию, которая приводит к выводу: в механике равновесие — это состояние покоя или движение по инерции, а в химической квантовой суперпозиции – это постоянство высших производных по времени.

 

Возникновение термодинамики спонтанных процессов и инфо-термодинамики задержалось на несколько десятилетий из-за игнорирования негэнтропии Шрёдингера и излишней привязанности к великолепной, но слишком простой, модели времени по Ньютону. Эта модель отрицает участие времени, как физического фактора, в формировании и развитии физических процессов. Время по Ньютону не имеет физически значимой точки отсчета.

 

В результате выясняется, что,  сама по себе, шкала времени не имеет смысла.

 

Неудивительно, что время по Эйнштейну является мнимой величиной. Фундаментальное значение имеет лишь производная по времени (скорость света).

 

На необходимость повышения информационного содержания понятия времени указывал и И. Пригожин [11], предлагая перейти от неопределенного понятия времени к оператору времени, связанному со Вторым началом термодинамики.

 

Работа [4] оказалась, по-видимому, первой, где был предложен оператор, получивший название «термодинамическое время». Стало очевидным, что присутствие в операторе информации о физически значимой точке начала отсчета придаёт понятию времени смысл и свойства функции состояния. В результате появилась возможность записать уравнение развития, инвариантное к природе изучаемого процесса, и доказать, что химические реакции достигают равновесного состояния за конечный кратчайший  отрезок времени.

 

В термодинамике точкой начала отсчета времени является момент достижения состояния равновесия или момент выхода из состояния равновесия. Фундаментальный физический смысл имеет продолжительность существования неравновесной системы, иначе говоря, «собственное время» неравновесной системы – термодинамическое время.

 

Понятие «термодинамическое время» может служить основой для формирования новой термодинамики на пути от термодинамики неравновесных процессов [1] до инфо-термодинамики [3].