ФИЗИЧЕСКАЯ ДЕМОГРАФИЯ: НЕЛОКАЛЬНОСТЬ ПРОДОЛЖИТЕЛЬНОСТИ ЖИЗНИ ЧЕЛОВЕКА

ВВЕДЕНИЕ

Явление нелокальности проявляется как взаимодействие (изменение состояния или свойств) дистанционно разделенных частиц или систем, при отсутствии гравитационных, электростатических, магнитных и других известных сил.

В литературе [1] не удалось найти даже предположения, что макро-нелокальность может оказаться в числе значимых факторов, управляющих распределением продолжительности жизни человека. Явления микро- и, особенно, макро-нелокальности остаются дискуссионными по причине трудностей с воспроизведением и необходимости сложной специальной аппаратуры для обнаружения явлений нелокальности.

Цель данной статьи – предложить вниманию исследователей пример макроскопической нелокальности в дискретной неэргодической системе с дистанционно разделенными элементами. Явление многократно воспроизведено, надежно зафиксировано и не требует сложной и дорогостоящей аппаратуры для наблюдения и изучения. Этим примером является нелокальность распределения продолжительности жизни в человеческой когорте (когортой называется сообщество одновозрастных существ).

 ИДЕНТИФИКАЦИЯ НЕЛОКАЛЬНОСТИ

По определению, любая система представляет собой целое, состоящее из взаимодействующих между собой элементов. Взаимодействие элементов приводит к возникновению некоторого системного свойства, которым не обладает каждый элемент в отдельности.

Физическая природа сил взаимосвязи или взаимодействия между элементами может быть различной. В каждом случае, это предмет отдельного исследования. Явление нелокальности мы понимаем как проявление взаимодействия между дистанционно разделенными элементами некоторой дискретной системы.

Квантовая нелокальность проявляется как синхронное изменение состояния пары одновозрастных фотонов независимо от разделяющего их расстояния.

Принято считать, что в человеческой когорте, члены которой разделены расстояниями в сотни и тысячи километров,  акты смерти (т.е. переходы из живого в неживое состояние) происходят независимо одно от другого, т.е. распределены во времени  случайным образом.

В термодинамическом смысле, естественная эволюция когорты живых существ относится к классу спонтанных неэргодических процессов. Их основной системной особенностью является развитие по энергетической траектории кратчайшего времени [2]. На этом основании выдвигаем гипотезу: системным свойством человеческой когорты является вымирание по энергетической траектории кратчайшего времени. Невольно вспоминаются слова Сергея Есенина: «Я пришел на эту землю, чтоб скорей её покинуть».

Экспериментальное доказательство эволюции человеческой когорты по траектории кратчайшего времени является достаточным основанием для идентификации распределения продолжительности жизни человека как неизвестного ранее проявления макроскопической нелокальности.

ТРАЕКТОРИЯ  КРАТЧАЙШЕГО  ВРЕМЕНИ

Инвариантное уравнение спонтанного неэргодического процесса развития имеет вид [2]:

                                   -ΔΦ = Φ⁽ⁿ⁺¹⁾ ∙ τ ⁿ⁺¹ / (n + 1)!,                                                                         (1)

где Φ – потенциал неравновесного состояния;

τ – термодинамическое время;

n = 2, 3.... – диссипативный порядок энергетической траектории,   численное значение которого в каждом случае подлежит экспериментальному определению.

Величина  -ΔΦ в уравнении (1) минимизирована в силу вариационного условия. В уравнении (1) только две симбатные переменные. На этом основании формулируем принцип кратчайшего времени:

Спонтанный неэргодически процесс идет по действительной энергетической траектории кратчайшего времени, совместимой со свойствами системы и с физическими условиями процесса.

Это положение согласуется с утверждениями других авторов например, [2] и [3], о следовании самопроизвольных процессов по пути кратчайшего времени,

Определим диссипативный порядок траектории, наиболее близкой к известной из механики брахистохроне. В декартовых координатах {x, y} брахистохрона имеет вид циклоиды

=x = a(ωt ─ sin ωt),

y = a(1 ─ cos ωt),

где t – время,  ω – циклическая частота.

Разлагая  sin ωt и cos ωt в ряд и ограничиваясь начальными членами,  получаем параметрическое уравнение циклоиды в фазовых координатах и, в конечном счете, уравнение движения:

                             x = (1/6 a²ω⁶ )∙(d²x/dt² )³ .                                                                        (2)

В случае траектории второго диссипативного порядка (n = 2), уравнение движения имеет аналогичный вид                    

                             Φ = [1/6 (Φ⁽³⁾)² ]∙(Φ⁽²⁾)³ .                                                                         (3)

Уравнения (2) и (3) совпадают при условии, что дифференцирование производится по нормированному термодинамическому времени.

Следовательно, брахистохрона (циклоида) практически совпадает с траекторией второго диссипативного порядка, по которой идут процессы в химических и биологических системах [2].

БРАХИСТОХРОННОЕ РАСПРЕДЕЛЕНИЕ

Найдем закон статистического распределения случайной величины (продолжительности жизни человека в когорте) при следующих исходных данных.

Неэргодическая система (когорта), состоящая из элементов с одинаковыми свойствами, за конечный интервал термодинамического времени, нормированный к интервалу τ^*[0, 2π], переходит из метастабильного в равновесное состояние по траектории кратчайшего времени.

Для траектории второго диссипативного порядка (n = 2, Φ⁽³⁾ = const) вымирание когорты сводится к задаче о брахистохроне с той особенностью, что движение по траектории совершается посредством дискретных шагов (случайных событий), соответствующих актам вымирания членов когорты. В термодинамическом смысле, вымирание – это переход отдельных элементов системы из неравновесного в равновесное состояние.

Допущение о тождественности свойств дискретных элементов системы исключает необходимость вычислять изменения потенциала неравновесного состояния ΔΦ. Достаточно знать пропорциональное значениям потенциала относительное количество (долю) элементов системы, совершивших переход в равновесное состояние.

 Это равносильно нормировке системы в целом к единице. Поэтому интеграл вероятностей и функция распределения (плотность вероятности) случайной величины имеют, соответственно, вид:

        F = Φ = (τ^* ─ sin τ^*)/2π,                                                                             (4)

        φ(τ^*) = dΦ/dτ^* = (1 ─ cosτ^*)/2π,                                                                   (5)

где τ^* - случайная величина продолжительности жизни элемента системы, нормированная к интервалу значений [0, 2π].

В отличие от нормального (гауссовского) распределения, брахистохронное распределение является монопараметрическим и ограничено конечными значениями случайной величины. Однако, на практике важно знать, что центральная часть брахистохронного распределения (на протяжении примерно 60% шкалы нормированной продолжительности жизни) почти совпадает с отрезком нормального распределения, имеющего параметры: среднее μ = π, среднеквадратичное отклонение   σ = 0,38π, дисперсия σ² = 0,144π² .                   

Необходимо отметить, что в уравнениях (4) и (5) отсутствуют какие-либо эмпирические или подгоночные коэффициенты, подобные кинетическим коэффициентам в уравнениях химической кинетики. Нормированное брахистохронное распределение является инвариантным (не зависит от свойств элементов системы и от числа  дискретных элементов в системе).

БРАХИСТОХРОННАЯ БУМАГА

Нами разработан новый вид диаграммной бумаги – брахистохронная бумага [2].

Брахистохронная бумага имеет вид прямоугольной координатной сетки. На оси абсцисс – линейная шкала значений случайной величины (времени жизни) элементов дискретной системы). На оси ординат – нелинейная шкала потенциала неравновесного состояния (или величин ему пропорциональных) в энергетических или относительных единицах (%). Нелинейная шкала соответствует уравнению (4), что обеспечивает выпрямление интегральной диаграммы неэргодического процесса.

Расположение экспериментальных точек на брахистохронной бумаге в виде прямой линии (или отрезка прямой) является необходимым и достаточным условием для идентификации траектории кратчайшего времени, соответствующей  неэргодическому процессу второго диссипативного порядка.

РАСПРЕДЕЛЕНИЕ ПРОДОЛЖИТЕЛЬНОСТИ ЖИЗНИ ЧЕЛОВЕКА   

В качестве наиболее достоверных и надежных исходных данных, подлежащих обработке и изучению, нами использованы результаты переписей населения, проводившихся в разное время и в разных странах. Для целей данного краткого сообщения, достаточное количество информации содержится в таблицах смертности, приведенных в книге Э. Россета [3]. Первую достоверную таблицу продолжительности жизни человека составил Э. Галлей. Он использовал предоставленный ему В. Лейбницем список умерших в г. Бреслау (Вроцлав) за период 1687 – 1691. Позднее данные  Э. Галлея обрабатывал П. Лаплас.

На Рис. 1 представлены когортные графики дожития во Франции, построенные в координатах рахистохронной бумаги {% живых – возраст}: 1 - ранняя французская таблица (XVIII в.), дополненная данными (□) таблицы Галлея (XVII в.); 2 - французская таблица (середина XX в.); 3 - гипотетическая "биологическая" таблица демографической службы ООН.

На брахистохронной бумаге экспериментальные точки расположились на отрезках прямых, соответствующих детскому, взрослому и пожилому возрасту. Это означает, что в любом возрасте распределение случайной величины (продолжительность жизни) удовлетворяет принципу кратчайшего времени.

Нелокальность продолжительности жизни человека идентифицирована и доказана с использованием данных переписей населения различных стран.

ОБСУЖДЕНИЕ

Прямые каждого возраста параллельны одна другой. Аномальным исключением является некоторое уменьшение наклона отрезка прямой старшего возраста на траектории 1 по сравнению с траекториями 2 и 3. Это означает, что в XVII веке скорость вымирания пожилых людей была в полтора раза меньше, чем в  XX веке. Причина аномалии неизвестна и подлежит выяснению. Возможно, несмотря на успехи медицины утерян какой-то фактор долголетия. Формально, пожилая группа когорты XVII века принадлежит другой генеральной совокупности случайных величин.

Каждая из трех траекторий  имеет два излома. Это  означает, что на протяжении жизни  организм человека дважды претерпевает скачкообразные возрастные изменения. Сформулируем неизвестную ранее закономерность, вносящую коренное изменение в биофизику продолжительности жизни человека:

Самопроизвольный процесс старения ведет человеческую когорту к полному вымиранию по энергетической траектории, совместимой с социальными, экономическими и информационными условиями жизни и состоящей из трех отрезков, каждый из которых удовлетворяет принципу кратчайшего времени, причем первый переход с одного отрезка траектории на другой происходит со скачкообразным изменением значения третьей производной по времени при достижении возраста 3-5 лет, а второй - при достижении возраста 55-60 лет.

Строго говоря, индивидуальная  продолжительность жизни не является случайной величиной. Продолжительностью жизни каждого человека влияет надорганизменный коррелирующий фактор. Реализуются только  случайности, которые совместимы с принципом кратчайшего времени.           

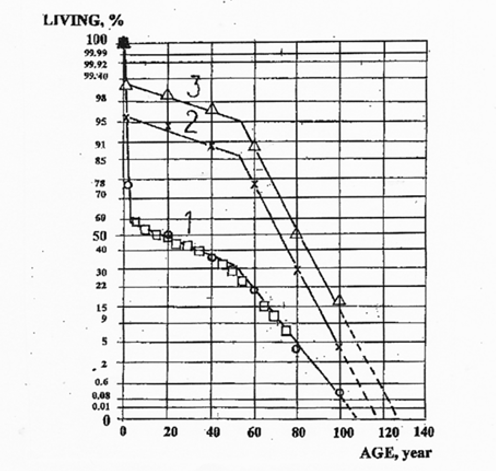
Рисунок. 1 Когортные графики дожития на брахистохроной бумаге (пояснения в тексте)

На брахистохроннй бумаге возрастные переходы выглядят как изломы прямых линий. Прямые линии свидетельствуют о выполнении принципа кратчайшего времени. Следовательно, продолжительность жизни каждого человека не является случайной. Все акты смерти взаимосвязаны. Продолжительность жизни задана еще до рождения человека. Успехи медицины лишь изменяют положение точек на тех же прямых. Для управления процессами демографии  требуется огромный объем дополнительных исследований.

С позиций термодинамики, возрастные  изменения организма человека похожи на фазовые переходы третьего рода с той особенностью, что скачкообразно изменяется третья производная по термодинамическому времени. Существование термодинамических постоянных в форме высших производных по времени, характеризующих свойства веществ и материалов в самопроизвольных процессах, доказано в статье [4].

Отметим еще одну интересную и важную закономерность. Биофизическими инвариантами продолжительности жизни человека оказались постоянные значения третьей производной Φ⁽³⁾ на каждом из  трех отрезков траектории жизни когорты, а также возраст 55 – 60 лет, соответствующий второму излому траектории. Эти инварианты визуально проявились благодаря монопараметрическому закону брахистохронного распределения.

ФИЗИЧЕСКАЯ ДЕМОГРАФИЯ – НОВОЕ НАПРАВЛЕНИЕ РАЗВИТИЯ ДЕМОГРАФИИ

Демография, как дисциплина, представляет собой научное исследование структуры, динамики и процессов воспроизводства населения. Предметом демографии является изучение закономерностей изменения численности, территориального размещения и состава населения, а также факторов, на них влияющих.

Теоретическое и экспериментальное доказательство нелокальности распределения продолжительности жизни человека сильно расширяет понимание фундаментальные закономерностей, управляющих демографическими процессами.

В контексте анализа демографических процессов, демография широко использует статистические методы и моделирование, опираясь на данные переписей населения, текущего учета демографических событий (рождений, смертей, браков, разводов) и выборочных обследований. Важным инструментом демографических исследований является построение демографических таблиц, таких как таблицы смертности, которые позволяют оценить показатели продолжительности жизни и вероятность смерти в различных возрастах [5]. В результате нашей работы, к физико-математическому арсеналу демографических исследований добавилось использование представлений и аппарата инфо-термодинамики [6].