РАЗРАБОТКА АЛГОРИТМОВ УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ БПЛА

В настоящее время наблюдается устойчивая тенденция к широкому применению БПЛА в различных секторах экономики – это обусловлено стремительным развитием технологий и потребностью в автоматизации процессов в таких областях, как логистика, сельское хозяйство, экологический мониторинг и другие. Современные беспилотники эффективно используются для доставки грузов, точечного опрыскивания сельскохозяйственных угодий, оперативного обнаружения и тушения лесных пожаров, а также для решения множества других задач.

Для описания динамики короткопериодических движений БПЛА самолетного типа в продольном канале, часто используется следующая система уравнений [1]:

,

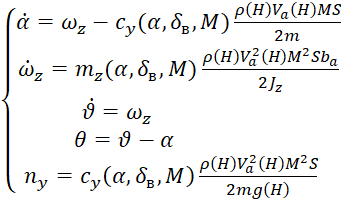Представленная система (1) обеспечивает высокоточное моделирование динамики БПЛА в вертикальной плоскости, что делает ее незаменимой основой для разработки эффективных систем стабилизации. Система стабилизации продольного канала построена таким образом, что ее параметры автоматически адаптируются к изменяющимся условиям полета, обеспечивая оптимальную производительность в любой ситуации. Формирование управляющего сигнала происходит на основе следующего закона [2]:

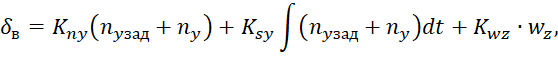
Несмотря на то, что данное уравнение представляет собой упрощенную модель динамики и структуры системы управления, оно позволяет проводить качественный анализ и синтез системы стабилизации на начальных этапах разработки, закладывая прочный фундамент для дальнейшей оптимизации и усовершенствования.

Вместе с тем, для достижения максимальной точности и эффективности системы управления, настоятельно рекомендуется использовать нелинейную модель БПЛА. Такой подход позволяет учесть все тонкости и нюансы, а также нелинейные характеристики системы, которые могут существенно влиять на ее поведение. Это особенно важно в условиях сложной динамики полета или при воздействии внешних возмущений.

Использование нелинейной модели гарантирует необходимое качество переходных процессов, минимизируя колебания и обеспечивая быстрое и плавное достижение заданных параметров. В контексте нелинейной модели перспективным направлением является применение современных алгоритмов глобальной оптимизации для поиска оптимальных значений коэффициентов передачи контура стабилизации. Эти алгоритмы позволяют эффективно исследовать сложное пространство параметров и находить решения, обеспечивающие наилучшие характеристики системы управления.

В этом случае задача сводится к оптимизации целевого критерия, отражающего требуемые характеристики замкнутой системы управления. Объект управления при этом рассматривается как «черный ящик», куда подаются коэффициенты передачи, а на выходе оценивается значение целевой функции. Преимуществом такого подхода является относительная простота учета различных особенностей системы, таких как нелинейности, эффект осцилляции или зоны нечувствительности привода.

В рамках данной работы критерий качества основан на минимизации квадратичной ошибки слежения контура стабилизации заданному эталону 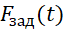. Робастность системы обеспечивается за счет плавности переходной характеристики. Критерии качества формализуются следующим образом:

1) Штраф за отклонение от заданного эталона :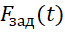

,

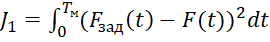где 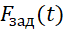,  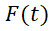– переходные процессы (желаемый/текущий соответственно);  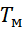– показатель времени моделирования.

2) Штраф за превышение 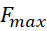 на  :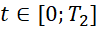

,

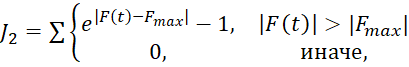где 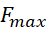    – допустимая максимальная величина переходного процесса.

3) Штраф за непопадание 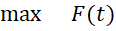   в :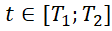

,

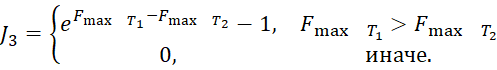где  ;   .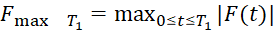

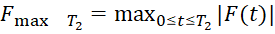4) Штраф за непопадание в трубку точности на :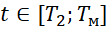

,

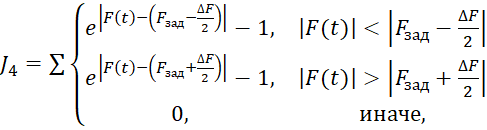где 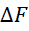 – трубка точности.

При использовании методов оптимизации без явного ограничения аргументов целевой функции предусмотрен дополнительный штраф:

,

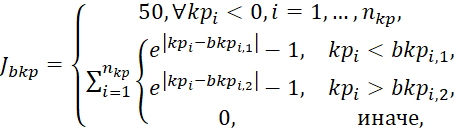где 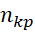– количество передаточных чисел; 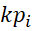– вектор передаточных чисел; 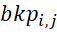– массив ограничений передаточных чисел, в первом столбце которого расположены нижние ограничения, во втором – верхние.

На основе рассмотренных критериев и штрафа, итоговая целевая функция представляется в виде:

,

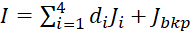где  – вектор из четырех элементов, значения которых равны 0 или 1 в зависимости от использования того или иного штрафа при формировании целевой функции.

Предложенный интегральный критерий оценки производительности, фактически, представляет собой взвешенную сумму нескольких ключевых показателей качества переходных характеристик в системе стабилизации с обратной связью. Подобная формулировка задачи оптимизации, как правило, приводит к мультимодальной задаче, характеризующейся наличием множества локальных экстремумов. Эффективный поиск глобального минимума в данном случае требует применения современных алгоритмов глобальной оптимизации, таких как методы, основанные на принципе роевого интеллекта.

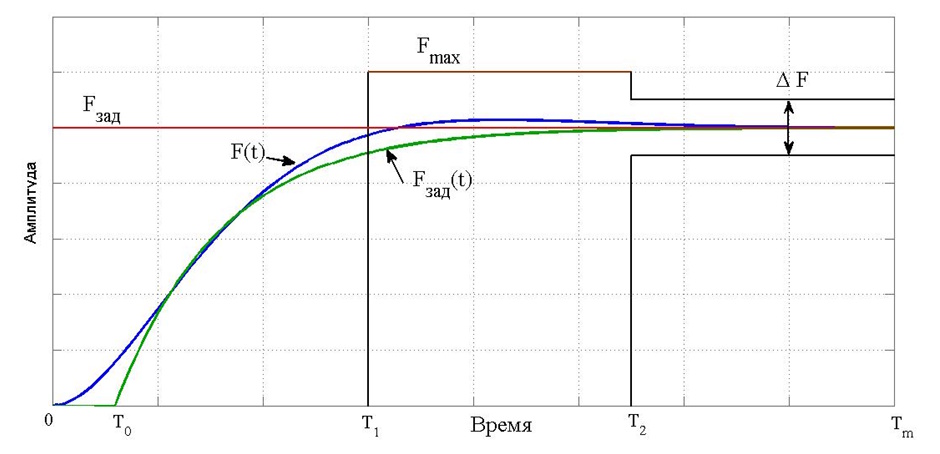
Рисунок 1. Наглядное представление элементов критериев качества

Ключевое отличие алгоритма роя частиц (PSO) от других популяционных методов заключается в отсутствии явного моделирования траектории поиска оптимального решения в пространстве параметров. Вместо этого, каждая частица, представляющая собой потенциальное решение, характеризуется двумя основными атрибутами: ее текущей координатой в пространстве поиска и ее «инерцией» – вектором скорости, определяемым взвешенным вкладом двух факторов: лучшей позиции, достигнутой данной частицей, и лучшей позиции, достигнутой всей популяцией. Совместное движение частиц обеспечивает исследование всего пространства поиска.

Фундаментальные принципы, лежащие в основе работы метода роя частиц, следующие [3]:

1. Стремление к оптимуму (инерция). Каждая частица стремится занять наиболее благоприятную позицию в пространстве поиска, основываясь на собственном опыте.
2. Коллективный разум (влияние популяции). Частицы учитывают информацию о наилучшей позиции, найденной всей популяцией, что способствует сходимости к глобальному оптимуму.
3. Социальное взаимодействие (влияние соседей). Предпочтения частицы формируются под воздействием решений, принятых ее ближайшими «соседями» в популяции, что позволяет избежать преждевременной сходимости и исследовать локальные области поиска более детально.

Позиция каждой частицы определяется ее вектором скорости, который корректируется в соответствии с принципами роевого интеллекта. Закон изменения скорости учитывает текущую скорость, коэффициент затухания и информацию о лучших позициях, найденных как самой частицей   , так и всей популяции . Математически, это выражается следующим образом:

,

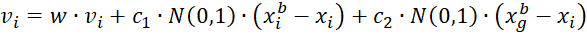где – положительные константы ускорения, определяющие степень влияния индивидуального и коллективного опыта; 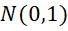– случайная величина, равномерно распределенная на отрезке 0 до 1 и вносящая элемент случайности в процесс обучения.

Для обеспечения сходимости алгоритма величина скорости частиц должна уменьшаться со временем. Это достигается путем введения коэффициента демпфирования, который определяет степень затухания скорости на каждой итерации. В простейшем случае используется линейная зависимость:

,

где  – положительная константа в диапазоне от 0 до 1, характеризующая интенсивность демпфирования.

Влияние коллективного разума и локальных взаимодействий учитывается на каждой итерации алгоритма путем выбора лучшей частицы. Процесс отбора можно представить следующим образом:

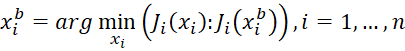
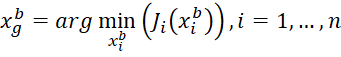
Ограничения на коэффициенты передачи в большинстве случаев задаются ограничительными рамками вектора решения в сегменте поиска:

,

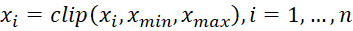где 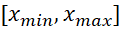 – границы поисковой области.

На Рисунке 2 представлен визуальный анализ результатов математического моделирования, демонстрирующий совокупность переходных процессов в исследуемом канале управления. Пунктирные линии на графике соответствуют эталонным сигналам, определенным для каждого конкретного режима полета.

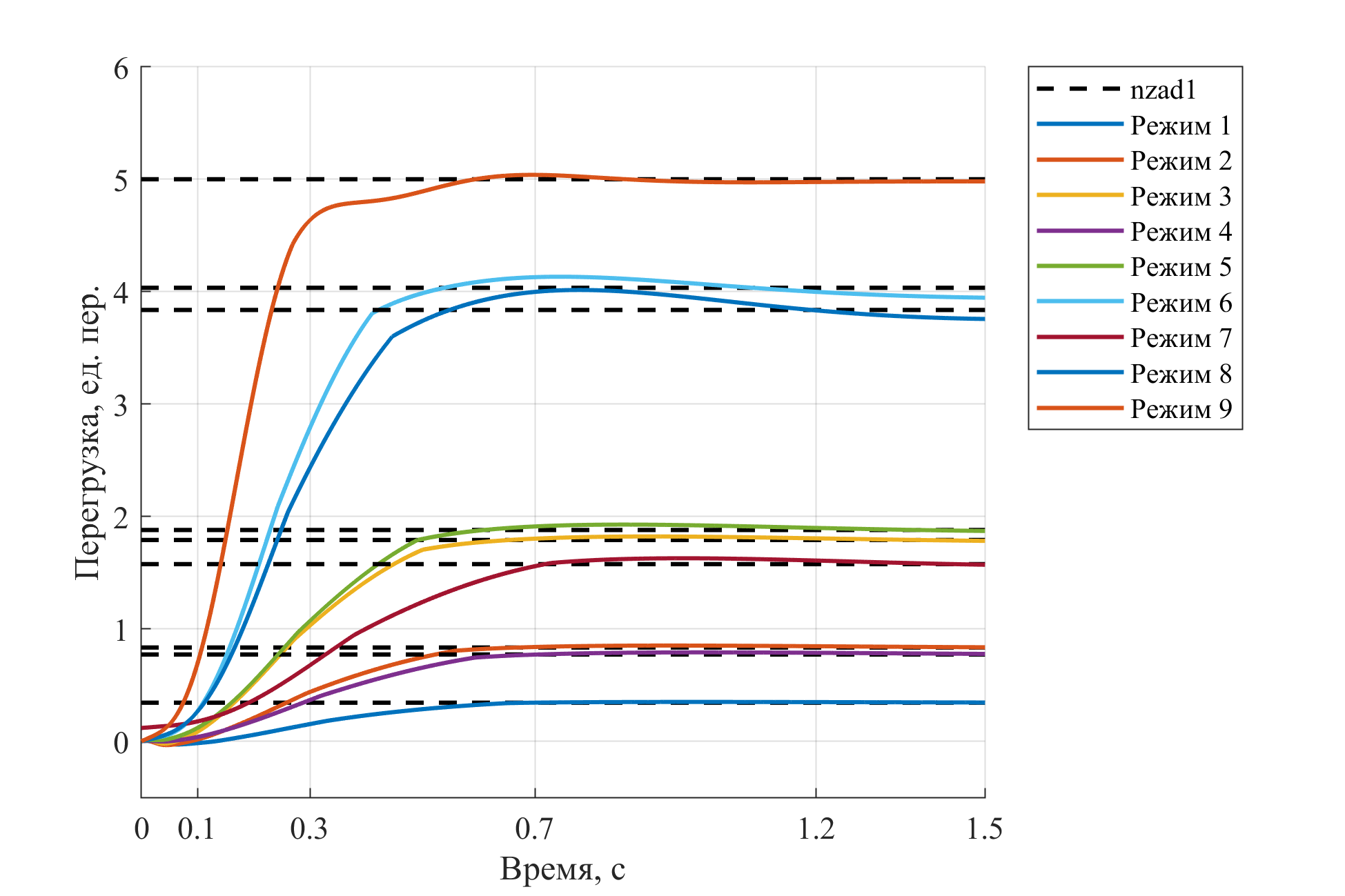
Рисунок 2. Семейство переходных процессов в вертикальном канале